n的阶乘是指从1连乘到n的结果,通常用符号n!表示。例如,3的阶乘表示为3!,计算过程如下:
3! = 3 × 2 × 1 = 6
一般地,n的阶乘可以用递归或迭代的方式计算,公式为:
n! = n × (n-1) × (n-2) × ... × 2 × 1
阶乘在数学和计算机科学中都有广泛的应用,例如在组合数学、排列组合、概率统计等领域。
那么勇java代码来实现,有哪些方式呢
第一种:迭代,这种是最直观最容易理解的:
private long factorial(int n) {
long factorial = 1;
while (n > 1) {
factorial = factorial * n;
n--;
}
return factorial;
}
@Test
public void factorial() {
System.err.println(factorial(1));
System.err.println(factorial(2));
System.err.println(factorial(3));
System.err.println(factorial(4));
System.err.println(factorial(5));
}第二种:递归,只要n不等于1,一直调用自身:
private long recursionFactorial(int n) {
if (n == 1) {
return n;
} else {
return n * recursionFactorial(n - 1);
}
}
@Test
public void recursionFactorial() {
System.err.println(recursionFactorial(1));
System.err.println(recursionFactorial(2));
System.err.println(recursionFactorial(3));
System.err.println(recursionFactorial(4));
System.err.println(recursionFactorial(5));
}第三种:使用栈或者队列来实现,递归的本质是在jvm层面的方法栈上创建栈帧来缓存中间结果,那么我们可以换一种思路,只要能把中间结果缓存起来,就可以不用递归了,其本质其实还是迭代:
private long stackFactorial(long n) {
Stack<Long> stack = new Stack<>();
stack.push(n);
long result = 1;
while (!stack.isEmpty()) {
Long pop = stack.pop();
result = result * pop;
if (pop > 1) {
pop--;
stack.push(pop);
}
}
return result;
}
@Test
public void stackFactorial() {
System.err.println(stackFactorial(1));
System.err.println(stackFactorial(2));
System.err.println(stackFactorial(3));
System.err.println(stackFactorial(4));
System.err.println(stackFactorial(5));
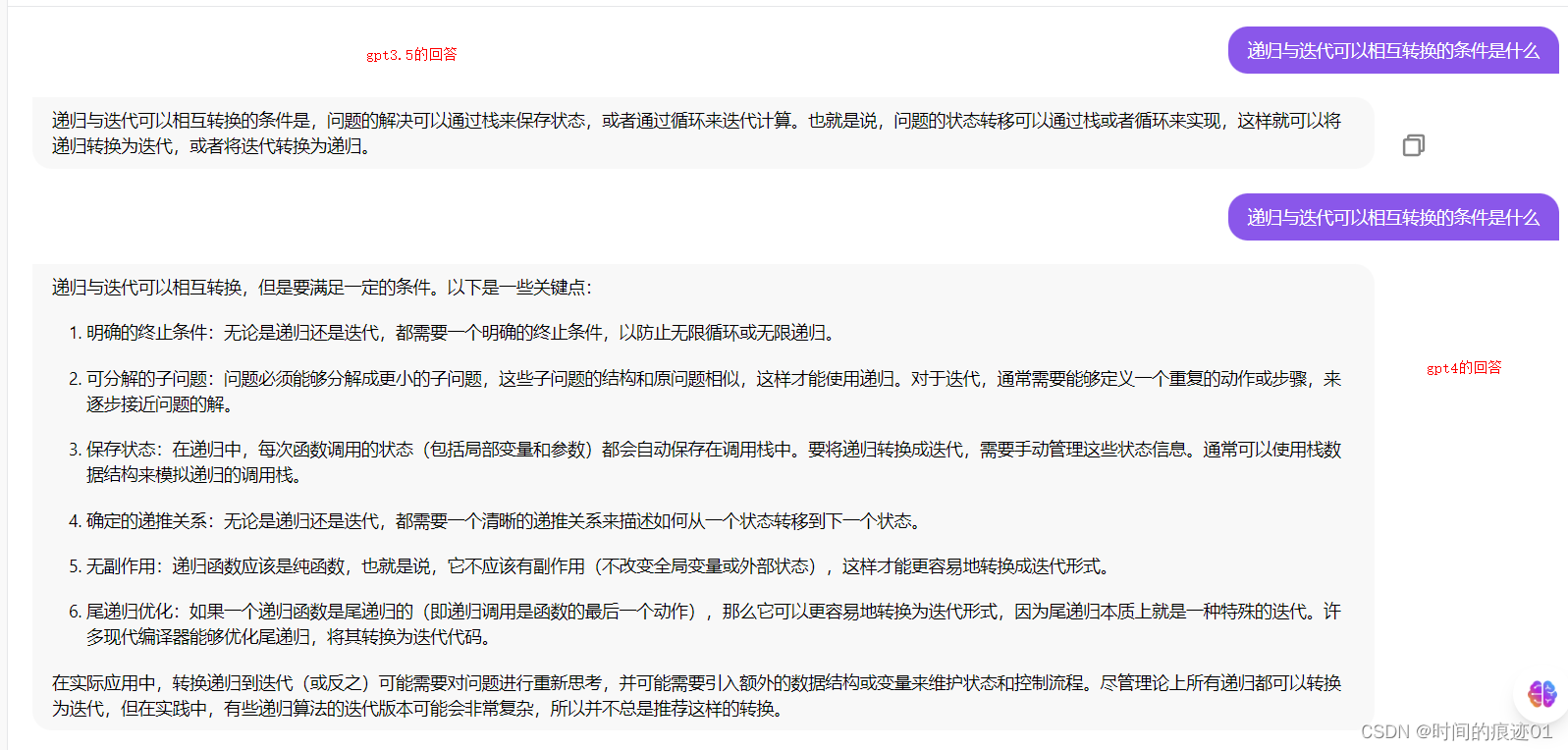
}总结:某些递归是可以通过迭代来实现的,那么递归和迭代能够相互转换的条件是什么呢,我们来看看不同的AI模型的回答
chatgpt:
讯飞星火:

腾讯混元:

百度AI:
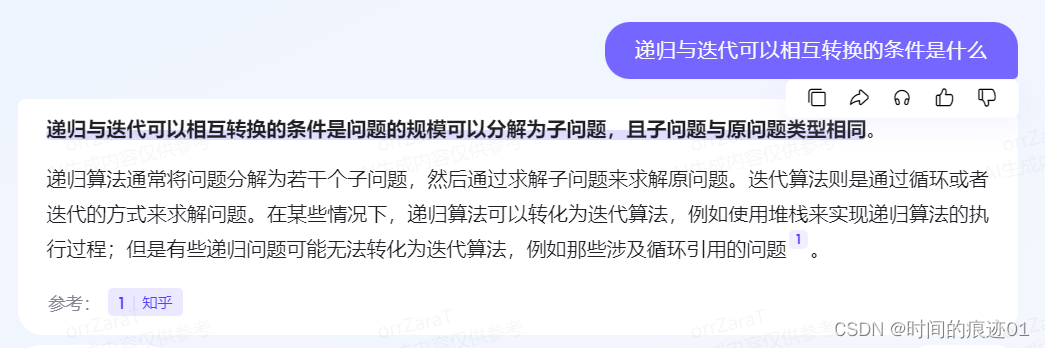
阿里通义千问:(这个截图不全,就贴文字了)
递归与迭代可以相互转换的条件通常基于问题本身的特性。在某些情况下,一个使用递归实现的问题可以通过重新组织代码和使用循环结构(如for、while等)来实现迭代版本。反过来,一些用迭代实现的问题也可能通过引入函数调用自身的方式来实现递归版本。
要判断一个问题是否可以递归与迭代之间转换,可以考虑以下几点:
-
可分解性:问题必须能够被分解为更小的同类子问题,这是递归的核心思想。同样,如果问题可以用循环来处理每个元素或状态,则可能适合迭代。
-
基本情况的存在:对于递归来说,需要存在一个或多个基本的情况,在这些情况下,不需要进一步递归。对于迭代来说,这通常是循环结束的条件。
-
合并子结果:无论是递归还是迭代,都需要一种方式将子问题的结果合并到整个问题的答案中。
-
问题规模的变化:在递归过程中,问题规模应该逐渐减小,最终达到基本情况。在迭代过程中,这通常表现为循环变量的变化。
-
空间和时间效率:虽然递归和迭代都可以解决同一问题,但它们的时间复杂度和空间复杂度可能会不同。在进行转换时,需要注意是否会影响算法的性能。
尽管大多数情况下递归与迭代可以相互转换,但也有一些特殊情况,比如涉及到特定数据结构(如树、图)的问题,或者一些复杂的动态规划问题,它们可能更适合于使用其中的一种方法,因为另一种方法可能会导致代码变得过于复杂且难以理解。因此,在实际编程中,选择哪种方法取决于具体问题以及对性能和代码可读性的要求。