详解线段树

news2024/11/26 3:29:00

前段时间写过一篇关于树状数组的博客树状数组，今天我们要介绍的是线段树，线段树比树状数组中的应用场景更加的广泛。这些问题也是在leetcode 11月的每日一题频繁遇到的问题，实际上线段树就和红黑树 、堆一样是一类模板，但是标准库里面并没有（所以题目的代码量会比较大）。如果我们深刻了解了其中的原理，刷到的时候默写出来问题也不是很大。

文章目录

  • 问题引入
  • 线段树的引入
  • 树节点数据结构
  • 建立一个线段树
  • 线段树的查询
  • 线段树的区间修改
  • 小结
  • Lazy标记
    • 区间修改
      • 向下传递
    • 代码
  • 动态开点
  • 完整模板
  • 总结
  • 例题：

如果没有看过线段树博客的先去看那个，再来看这个问题

问题引入

在树状数组中我们的问题是：

给你一个数组 nums ，请你完成两类查询。
其中一类查询要求 更新 数组 nums 下标对应的值
另一类查询要求返回数组 nums 中索引 left 和索引 right 之间（ 包含 ）的nums元素的 和 ，其中 left <= right
实现 NumArray 类：

  • NumArray(int[] nums) 用整数数组 nums 初始化对象
  • void update(int index, int val) 将 nums[index] 的值 更新 为 val
  • int sumRange(int left, int right) 返回数组 nums 中索引 left 和索引 right 之间（ 包含 ）的nums元素的 和 （即，nums[left] + nums[left + 1], …, nums[right]）

在这个问题中我们对区间的修改始终是单点修改，如果我们想修改一个区间的值（指给这个区间的所有值都加、减一个数），这时候树状数组只能遍历这个区间，然后对区间每一个数做单点修改，这样修改的时间复杂度就是M*logN，M为区间长度，N为整个区间的大小。

但是如果用线段树来解决，每次区间修改的时间复杂度可以降到logN

线段树的引入

线段树不像前面介绍的树状数组一样，树状数组逻辑结构是树，但是物理结构是一个数组。而线段树是一个真正的树型结构。
假设我们有一个长度为10 的数组。如果我们要构建一个线段树一定是下面这个结构：
在这里插入图片描述
我们观察可以发现：

  • 每个节点都是维护的一个区间的统计值（可以是区间和 区间的最大值 、最小值）
  • 所有的叶子节点的区间长度均为1，也就是数组的一个单点元素的值
  • 如果一个节点有子节点，且区间为[left,right] ,那么子节点的区间分别为[left,mid]、[mid+1,right] 其中mid=(left+right)/2

树节点数据结构

根据上图我们很轻松的就可以定义出树节点的数据结构。

struct STNode {
    STNode* left;    // 左节点
    STNode* right;   // 右节点
    int val;    // 维护的区间的值（可能是区间和、区间的最值）
    int add;  //这个是lazy标记，我们后面会介绍，这里我们可以先忽略
};

建立一个线段树

实际上这个建立树的过程，后面会讲到线段树的动态开点，否则leetcode的内存会爆掉。
假设我们给定一个数组，要求你根据这个数组构建一个线段树，这个线段树的每一个区间维护的都是这个区间的区间和。


class SegmentTree {
public:
    void PushUp(STNode *cur) {
        cur->val = cur->left->val + cur->right->val;
    }
    void BuildTree(const vector<int>& v) {
        N = v.size();  // 用于记录线段树查询区间的大小
        function<void(int,int,STNode*&)> dfs = [&](int l,int r,STNode*& cur) {
            if (l == r) {
                cur=new STNode{ nullptr,nullptr,v[l],0};
                return;
            }
            int mid = (r - l) / 2 + l;
            cur=new STNode{ nullptr,nullptr,0,0 };
            dfs(l, mid, cur->left);
            dfs(mid + 1, r, cur->right);

            PushUp(cur);
        };

        dfs(0, v.size() - 1, root);
    }
private:
    STNode* root = nullptr;   // 根节点
    int N;                    // 用于记录线段树查询区间的大小
};

注意这个递归建立线段树，一定要选对遍历的方式——后续遍历，因为只要一个节点有子节点，那么他的值一定是在两个子节点已经遍历完了之后才能确定，这符合后续遍历的定义：先遍历完左子树和右子树，最后两个子树的信息汇总到根节点。
这样一颗完整的线段树便可以确定。注意这里的PushUp函数就是遍历完左右子树后的更新根节点，由于后面的查询和区间修改都需要这个操作所以这里需要重点理解一下！

线段树的查询

线段树查询的思路是：

假设被查询的区间是[left,right] ,当前节点的区间为 [start , end]

  • 如果查询的区间正好包括了节点所代表的区间，即left <=start && right>=end 则返回区间的值
  • 如果查询的区间不包含节点的区间，那么我们可以通过 mid = (start +end)/2 求出其两个子节点的区间，然后将判断查询区间和哪个子节点相交，继续向子节点向下递归,直到找到第一种情况为止

对于区间查询，比方说我们需要查询[2,6]这个区间的区间和，红色的是查询的路径，蓝色是最终组成这个[2,6]区间的节点，也是查询的结束的地方。
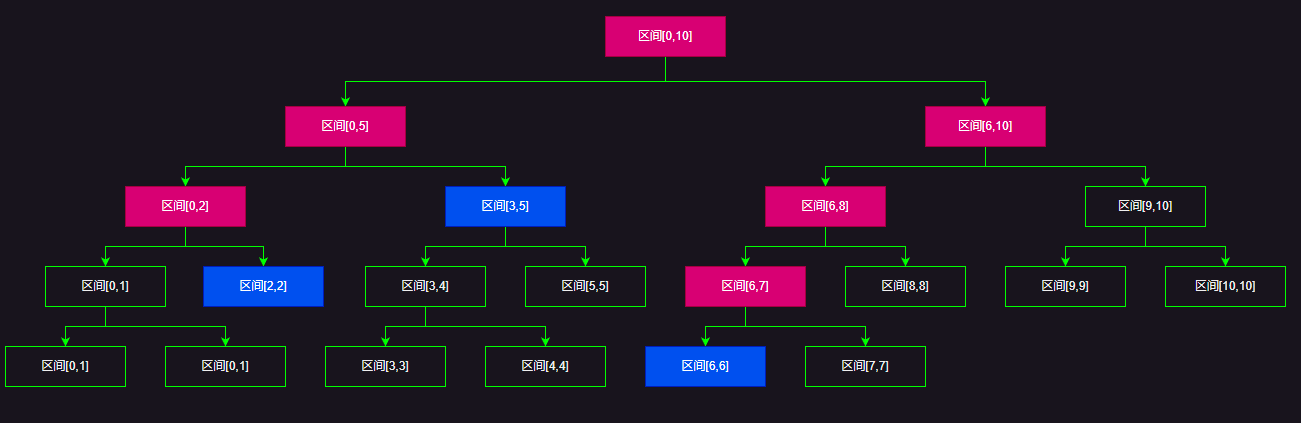
在这里插入图片描述

很简单，我们顺着上面的逻辑很快就能写出查询某个区间的代码，这里就不做过多的解释了

class SegmentTree {
public:
    void PushUp(STNode *cur) {
        cur->val = cur->left->val + cur->right->val;
    }
    // 区间查询
    int Query(int left,int right) {
        // left right 为要查询的区间   start end 为当前节点所维护的区间
        function<int(int, int, int, int, STNode*)> dfs = [&](int left, int right,int start ,int end, STNode* cur) {
            if (left <= start && right >= end) {
                return cur->val;
            }
            int mid = (end - start) / 2 + start;
            int ansl = 0, ansr = 0;
            if (left > mid) {
                ansl = dfs(left, right, mid + 1, end, cur->right);
            }
            else if (right <=mid) {
                ansr = dfs(left, right, start, mid, cur->left);
            }
            else {
                ansl = dfs(left, right, mid + 1, end, cur->right);
                ansr = dfs(left, right, start, mid, cur->left);
            }
            //PushUp(cur);   // 向上更新
            return ansl + ansr;
        };
        return dfs(left, right, 0, N, root);
    }
private:
    STNode* root = nullptr;   // 根节点
    int N;                    // 用于记录线段树查询区间的大小
};

线段树的区间修改

这里我们讨论的区间修改只的是让区间[left,right] 都加上或减去一个val
到这里我们来分析一下如何进行区间修改，这里我们和区间查询的思路一致：

假设被查询的区间是[left,right] ,当前节点的区间为 [start , end]

  • 如果查询的区间正好包括了节点所代表的区间，即left <=start && right>=end 则更新区间的值，但是这里注意，我们更新了大区间的值，下面他的所有小区间都需要更新 ，下面的代码PushDown函数就是处理这个问题的。
  • 如果查询的区间不包含节点的区间，那么我们可以通过 mid = (start +end)/2 求出其两个子节点的区间，然后将判断查询区间和哪个子节点相交，继续向子节点向下递归，直到找到第一种情况为止
class SegmentTree {
public:
    void PushUp(STNode *cur) {
        cur->val = cur->left->val + cur->right->val;
    }
    void PushDown(int l,int r,STNode* cur,int val) {
        if (cur == nullptr) {
            return;
        }
        cur->val += (r - l+1) * val;
        int mid = (r - l) / 2 + l;
        PushDown(l, mid, cur->left, val);
        PushDown(mid + 1, r, cur->right, val);

    }
    void Update(int left, int right,int val) {
        // left right 为要查询的区间   start end 为当前节点所维护的区间  val为区间修改的值
        function<void(int, int, int, int, int, STNode*)> dfs = [&](int left, int right, int start, int end, int val, STNode* cur) {
            if (left <= start && right >= end) {
                PushDown(start, end, cur, val);  // 将cur区间所有子节点全部更新了
                return;
            }
            int mid = (end - start) / 2 + start;
            int ansl = 0, ansr = 0;
            if (left > mid) {
                dfs(left, right, mid + 1, end, val, cur->right);
            }
            else if (right <= mid) {
                dfs(left, right, start, mid, val, cur->left);
            }
            else {
                dfs(left, right, mid + 1, val, end, cur->right);
                dfs(left, right, start, mid, val, cur->left);
            }
            PushUp(cur);   // 向上更新 值，因为修改了子区间 其所有父区间都会被修改！
         };
        dfs(left, right, 0, N,val, root);
    }
private:
    STNode* root = nullptr;   // 根节点
    int N;                    // 用于记录线段树查询区间的大小
};

小结

代码写到这里，线段树的功能已经被我们全部实现了，但是我们回国头来看一下线段树的实现思路，看看是否还有优化的地方。
我们主要把目光放在 线段树的修改上面，我们上面线段树的修改的思路实际上和树状数组的遍历区间的单点修改是没有什么区别的，并没有什么优势，时间复杂度都是：时间复杂度就是M*logN，M为区间长度，N为整个区间的大小。
所以我们接下来要介绍一下优化方案——Lazy标记

Lazy标记

区间修改

我们的区间修改 的优化方案 主要集中在PushDown这个函数上，我们当前的区间修改，对于节点的区间被查询区间包含的情况，是修改当前节点，并将修改传递给当前节点的每一个子节点。而我们的Lazy标记实际上就是优化这一步。

实际上我们发现我们修改完当前的节点时候（对于节点的区间被查询区间包含的情况），实际上并不需要将子节点修改，或者换一种说法：不需要立刻修改所有的子节点，我们可以设置一个Lazy标记。
这个Lazy标记的定义是：
记录所有子节点的区间应当被修改，但是未被修改的值。（这些值先由父节点记录，等到后面如果要访问到下面的节点的时候，顺路把标记带下去）
这些懒标记，我们可以在后面查询的时候，比方说访问到懒标记所在节点的子节点的时候，在去把Lazy标记下放，也就是把Lazy标记传递到子节点。

假设我有一个全0的长度位10 的数组，需要更新区间[0,6]
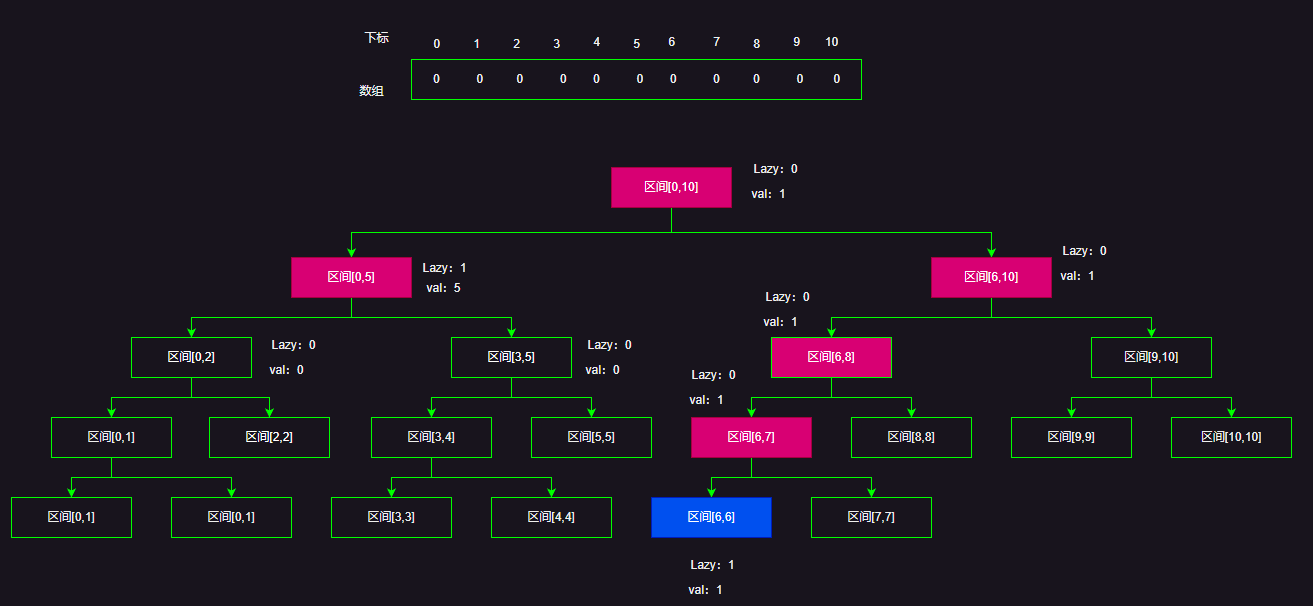
在这里插入图片描述

这时候按照 Lazy标记的 定义，我们遍历到区间包含节点区间的时候，就不必向下更新了，而是直接修改节点的Lazy标记，
这样
我们回过头来看，树节点的设计中我们一直都留着一个add，这个就是每个树节点的Lazy标记

struct STNode {
    STNode* left;
    STNode* right;
    int val;
    int add; // Lazy标记
};

我们更新[0,6]这个区间，递归结束的节点始终满足节点区间被查询区间所包含，注意更新的值为：区间长度*val

但是别忘了最后的回溯更新，所以这次区间更新的最终结果是，黄色的线代表回溯更新的路线

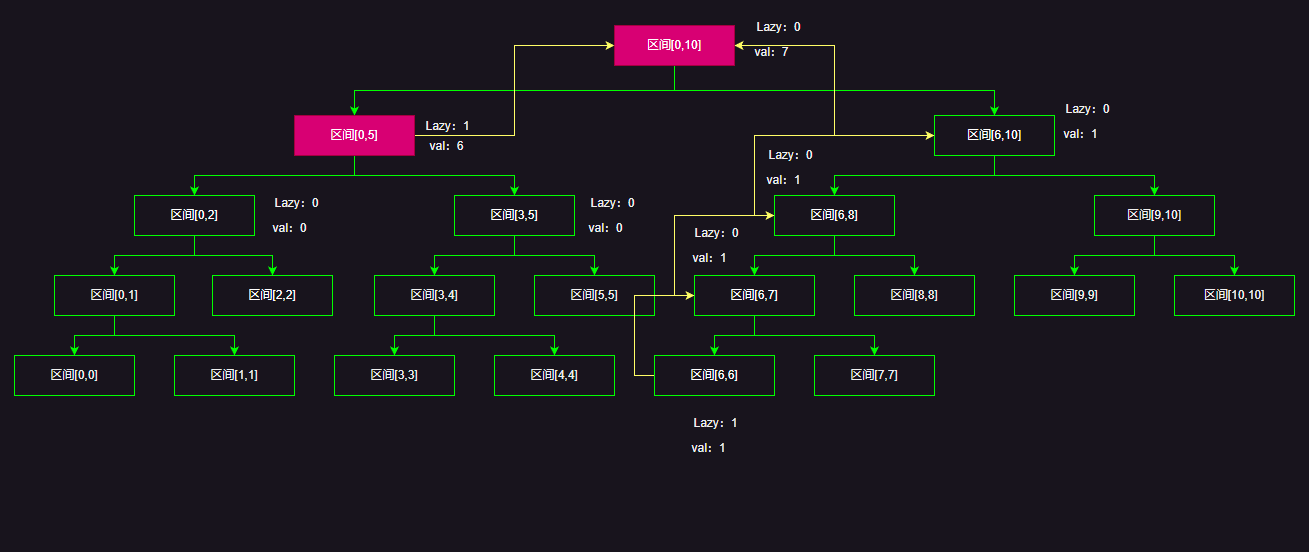
在这里插入图片描述

向下传递

假设我们这时候需要查询或者更新[0,2]
我们这里以更新区间[0,2]，让区间里面的每一个元素加1为例：

当我们遍历到区间[0,2]的时候，这时候就需要下放Lazy标记到他的子节点，注意这里下放的Lazy标记代表节点区间[0,2]和节点区间[3,5]理论上应该区间每一个元素+1，所以每个节点的val需要+3，然后两个子节点lazy标记需要加上父节点的Lazy标记（注意不是直接赋值），因为这两个子节点的子节点并没有更新Lazy标记。最后记得把父节点区间[0,5]的lazy标记置0！
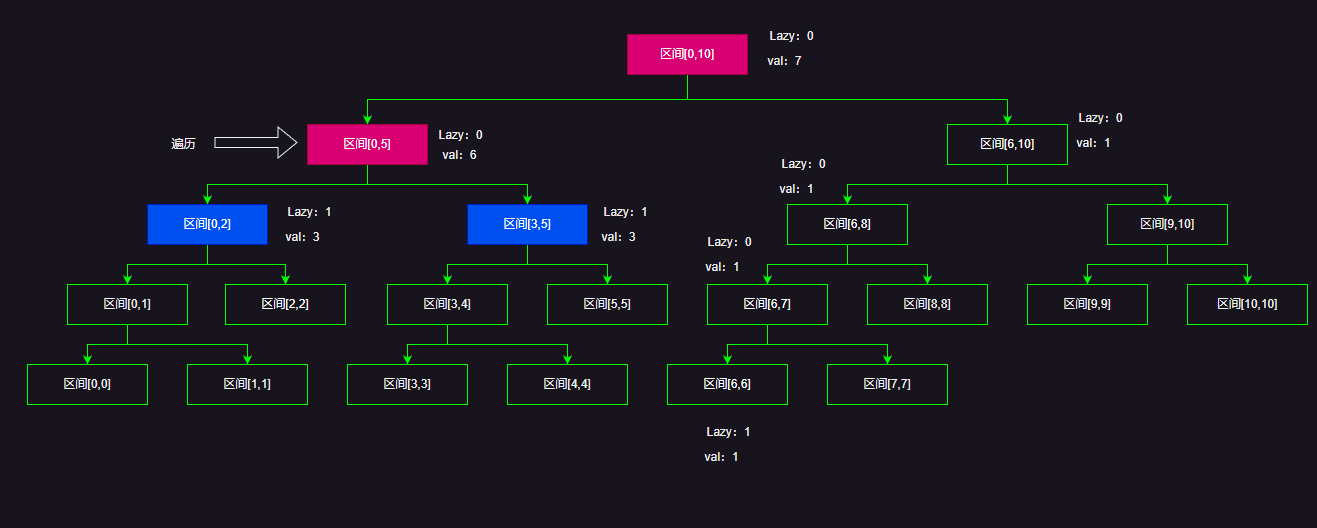
在这里插入图片描述

然后由于我们还需要更新[0,2]节点的值，所以我们直接更新节点区间[0,2]lazy标记，让Lazy标记+=1（因为要更新区间[0,2]让区间每一个元素加1）
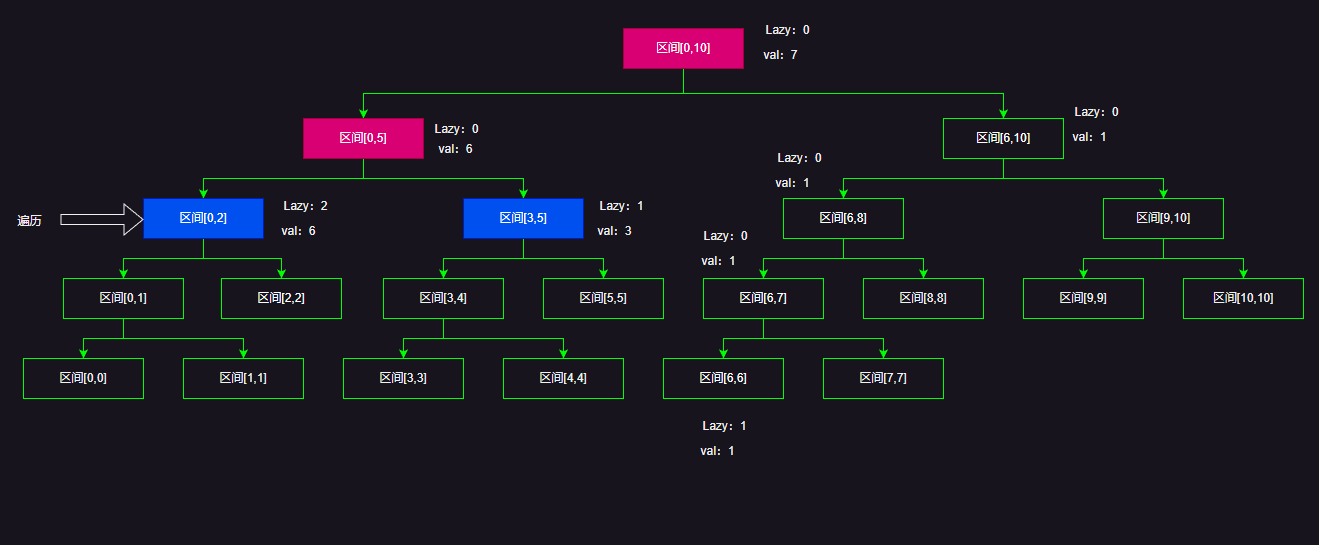
在这里插入图片描述

最后别忘了回溯的时候更新父节点的val！
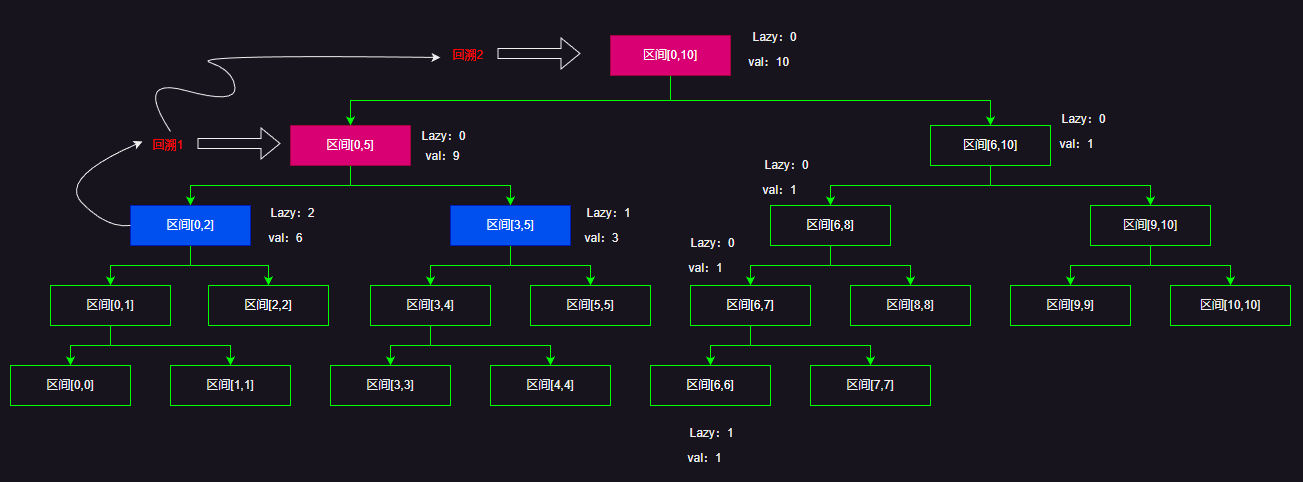
在这里插入图片描述

代码

从上面的流程我们可以看出，Lazy标记实际上是一种向下传递，所以我们只需要修改PushDown函数的逻辑既可，那我们就要思考一个问题：何时需要向下传递？
答案很简单：当查询区间不包含当前节点区间的时候，这时候查询的区间一定在当前区间的子节点中，所以需要向下递归，所以在向下递归之前我们需要下传Lazy标记！
这句话需要好好理解一下。

   void PushDown(int l, int r, STNode* cur) {
       if (cur->add == 0)   // 如果当前节点没有Lazy标记，则不需要下传直接返回
           return;
       int mid = (r - l) / 2 + l;
       // 将父节点的 Lazy 标记下传到
       cur->left->add += cur->add;
       cur->right->add += cur->add;
       cur->left->val += (mid - l + 1) * cur->add;
       cur->right->val += (r - mid) * cur->add;
       cur->add = 0;
   }

然后相应的Query和Update函数都要做出相应的修改

   void Update(int left, int right, int val) {
       // left right 为要查询的区间   start end 为当前节点所维护的区间  val为区间修改的值
       function<void(int, int, int, int, int, STNode*)> dfs = [&](int left, int right, int start, int end, int val, STNode* cur) {
           if (left <= start && right >= end) {
               cur->val += (end - start + 1) * val;
               cur->add += val;
               return;
           }
           // 走到这里代表要查询的区间[left,right]一定在cur节点的子节点中！ 一定要理解！！！！！
           PushDown(start, end, cur);
           int mid = (end - start) / 2 + start;
           int ansl = 0, ansr = 0;
           if (left > mid) {
               dfs(left, right, mid + 1, end, val, cur->right);
           }
           else if (right <= mid) {
               dfs(left, right, start, mid, val, cur->left);
           }
           else {
               dfs(left, right, mid + 1, end, val, cur->right);
               dfs(left, right, start, mid, val, cur->left);
           }
           PushUp(cur);   // 向上更新父节点
           };
       dfs(left, right, 0, N, val, root);
   }

   int Query(int left, int right) {
       // left right 为要查询的区间   start end 为当前节点所维护的区间
       function<int(int, int, int, int, STNode*)> dfs = [&](int left, int right, int start, int end, STNode* cur) {
           if (left <= start && right >= end) {
               return cur->val;
           }
            // 走到这里代表要查询的区间[left,right]一定在cur节点的子节点中！ 一定要理解！！！！！
           PushDown(start, end, cur);
           int mid = (end - start) / 2 + start;
           int ansl = 0, ansr = 0;
           if (left > mid) {
               ansl = dfs(left, right, mid + 1, end, cur->right);
           }
           else if (right <= mid) {
               ansr = dfs(left, right, start, mid, cur->left);
           }
           else {
               ansl = dfs(left, right, mid + 1, end, cur->right);
               ansr = dfs(left, right, start, mid, cur->left);
           }
           PushUp(cur);
           return ansl + ansr;
           };
       return dfs(left, right, 0, N, root);
   }

动态开点

到这里实际上线段树就已经结束了，但是做题的时候如果这样搞理论上应该是无法通过的，因为题目的区间都是很大的，一般题目给的区间都是[1,1000000000]，如果我们按照上面的构建线段树的方法，内存应该无法通过。与是这里我们又有了一种新的方法——动态开点

我们设想如果我们要查询的区间落在[1,1000000000]上，如果我们上来就开辟1000000000个节点构成线段树，设想下面这种情况，我们的区间查询和更新都集中在[0,5000000000] 上，而区间[500000001,1000000000]只被查询过一次，那么区间[500000001,1000000000]下面500000000个节点实际上是不用开辟的！
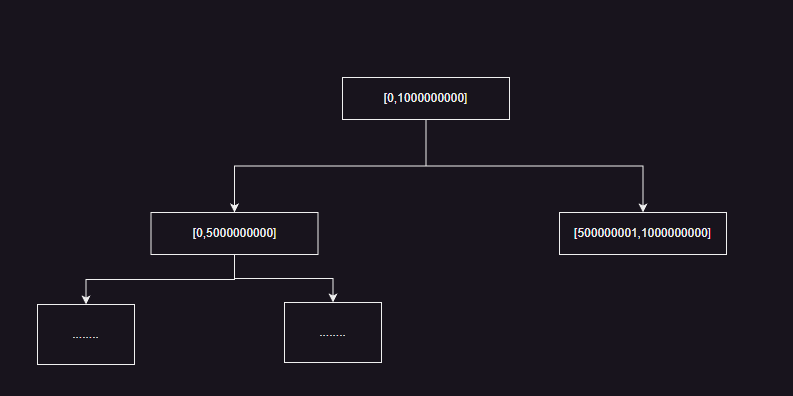
在这里插入图片描述

空间上是极大的浪费，我们这里的处理的方法和Lazy标记一样：就是当我们用到该节点的时候，我们再去创建该节点。
而我们何时知道需要访问到子节点？
也就是查询区间不包含当前节点区间的时候，意味着目标节点肯定在子节点中，这时候我们再去开辟子节点
我们把这部分逻辑放在PushDown函数里面去实现。


    void PushDown(int l, int r, STNode* cur) {
    	// 创建子节点 如果没有的话
        if (cur->left == nullptr) cur->left = new STNode{ nullptr,nullptr,0,0 };
        if (cur->right == nullptr) cur->right = new STNode{ nullptr,nullptr,0,0 };

        if (cur->add == 0)
            return;
        int mid = (r - l) / 2 + l;
        cur->left->add += cur->add;
        cur->right->add += cur->add;
        cur->left->val += (mid - l + 1) * cur->add;
        cur->right->val += (r - mid) * cur->add;
        cur->add = 0;
    }

完整模板

到这里线段树的模板就已经写完了😎

struct STNode {

    STNode* left;
    STNode* right;
    int val = 0;
    int add;
};



class SegmentTree {
public:

    void PushUp(STNode* cur) {
        cur->val = cur->left->val + cur->right->val;
    }

    SegmentTree() {
        N = 1000000000;
        root = new STNode{ nullptr,nullptr,0,0 };
    }


    void PushDown(int l, int r, STNode* cur) {
        if (cur->left == nullptr) cur->left = new STNode{ nullptr,nullptr,0,0 };
        if (cur->right == nullptr) cur->right = new STNode{ nullptr,nullptr,0,0 };

        if (cur->add == 0)
            return;
        int mid = (r - l) / 2 + l;
        cur->left->add += cur->add;
        cur->right->add += cur->add;
        cur->left->val += (mid - l + 1) * cur->add;
        cur->right->val += (r - mid) * cur->add;
        cur->add = 0;
    }


    void Update(int left, int right, int val) {
        // left right 为要查询的区间   start end 为当前节点所维护的区间  val为区间修改的值
        function<void(int, int, int, int, int, STNode*)> dfs = [&](int left, int right, int start, int end, int val, STNode* cur) {
            if (left <= start && right >= end) {
                cur->val += (end - start + 1) * val;
                cur->add += val;
                return;
            }
            PushDown(start, end, cur);
            int mid = (end - start) / 2 + start;
            int ansl = 0, ansr = 0;
            if (left > mid) {
                dfs(left, right, mid + 1, end, val, cur->right);
            }
            else if (right <= mid) {
                dfs(left, right, start, mid, val, cur->left);
            }
            else {
                dfs(left, right, mid + 1, end, val, cur->right);
                dfs(left, right, start, mid, val, cur->left);
            }
            PushUp(cur);
            };
        dfs(left, right, 0, N, val, root);
    }

    int Query(int left, int right) {
        // left right 为要查询的区间   start end 为当前节点所维护的区间
        function<int(int, int, int, int, STNode*)> dfs = [&](int left, int right, int start, int end, STNode* cur) {
            if (left <= start && right >= end) {
                return cur->val;
            }
            PushDown(start, end, cur);
            int mid = (end - start) / 2 + start;
            int ansl = 0, ansr = 0;
            if (left > mid) {
                ansl = dfs(left, right, mid + 1, end, cur->right);
            }
            else if (right <= mid) {
                ansr = dfs(left, right, start, mid, cur->left);
            }
            else {
                ansl = dfs(left, right, mid + 1, end, cur->right);
                ansr = dfs(left, right, start, mid, cur->left);
            }
            PushUp(cur);
            return ansl + ansr;
            };
        return dfs(left, right, 0, N, root);
    }


private:
    STNode* root = nullptr;   // 根节点
    int N;                    // 用于记录线段树查询区间的大小
};

总结

但是在做题的时候还是会对模板进行修改，修改的点主要在区间val的意义上，我们这里模板里面val代表的是区间和，但后面题目里面可能是 区间最大值 、区间最小值…，但是万变不离其宗，线段树的结构是不会变的。

例题：

我的日程安排表 1
我的日程安排表 II
我的日程安排表 III
715. Range 模块

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1292126.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Linux篇之在Centos环境下搭建Nvidia显卡驱动

Linux篇之在Centos环境下搭建Nvidia显卡驱动

一、前提条件 1、首先确认内核版本和发行版本&#xff0c;再确认显卡型号 uname -a // Linux localhost.localdomain 4.18.0-408.el8.x86_64 #1 SMP Mon Jul 18 17:42:52 UTC 2022 x86_64 x86_64 x86_64 GNU/Linux1.2 cat /etc/redhat-release // CentOS Stream release 81.3…
阅读更多...
logback日志框架使用

logback日志框架使用

依赖引入 <dependency><groupId>ch.qos.logback</groupId><artifactId>logback-classic</artifactId><version>1.1.7</version> </dependency> 使用logback日志框架只需要引入以上即可&#xff0c;(我们平时使用较多的Slf4j…
阅读更多...
获取Github Copilot的Token

获取Github Copilot的Token

可以在线提取出Github Copilot插件的Token&#xff0c;这样的话就可以把Token拿来做别的用处了&#xff0c;比如共享给其他人 Github Copilot是一款由GitHub和OpenAI合作开发的人工智能编程助手。它利用机器学习和自然语言处理技术&#xff0c;能够根据用户的输入自动生成代码…
阅读更多...
使用DockerUI结合内网穿透工具轻松实现公网访问和管理docker容器

使用DockerUI结合内网穿透工具轻松实现公网访问和管理docker容器

文章目录 前言1. 安装部署DockerUI2. 安装cpolar内网穿透3. 配置DockerUI公网访问地址4. 公网远程访问DockerUI5. 固定DockerUI公网地址 前言 DockerUI是一个docker容器镜像的可视化图形化管理工具。DockerUI可以用来轻松构建、管理和维护docker环境。它是完全开源且免费的。基…
阅读更多...
Python小案例：while练习题

Python小案例：while练习题

目录 while练习题&#xff1a;1、存款多少年能翻倍2.小球坠落长度计算3、猴子吃桃4、计算&#xff1a;1-23-4...99-100的和 while练习题&#xff1a; 1、存款多少年能翻倍 1万本金&#xff0c;年利息&#xff1a;0.0325&#xff0c;求连本带息多少年能翻倍 解析&#xff1a;…
阅读更多...
IP地址定位技术的原理与应用

IP地址定位技术的原理与应用

在当今的数字化时代&#xff0c;我们的在线活动每时每刻都在生成大量数据。其中&#xff0c;IP地址作为网络设备在互联网上的唯一标识&#xff0c;提供了一种独特的方式来追踪和定位这些活动。本文将深入探讨IP定位技术的原理及其在现实生活中的应用。 IP定位技术的原理 IP地址…
阅读更多...
【Hive】——概述

【Hive】——概述

1 什么是Hive 2 Hive 优点 3 Hive和Hadoop 的关系 4 映射信息记录 5 SQL语法解析、编译 Hive能将一个文件映射成为一张表&#xff0c;文件和表之间的关系称为映射 Hive的功能职责是将SQL语法解析编译成为MapReduce 6 Hive 架构 6.1 分析 6.2 架构图 6.3 用户接口 6.4 元数据存…
阅读更多...
通信线缆是什么

通信线缆是什么

通信线缆 电子元器件百科 文章目录 通信线缆前言一、通信线缆是什么二、通信线缆的类别三、通信线缆应用实例四、通信线缆的作用原理总结前言 每种线缆都有其特定的特性和用途。通信线缆起到连接和传输信号的作用，是实现通信和数据传输的重要组成部分。 一、通信线缆是什么 …
阅读更多...
评论送书：一本书讲透Java线程：原理与实践

评论送书：一本书讲透Java线程：原理与实践

摘要&#xff1a;互联网的每一个角落&#xff0c;无论是大型电商平台的秒杀活动&#xff0c;社交平台的实时消息推送&#xff0c;还是在线视频平台的流量洪峰&#xff0c;背后都离不开多线程技术的支持。在数字化转型的过程中&#xff0c;高并发、高性能是衡量系统性能的核心指…
阅读更多...
春风十里不如你——掌握Spring Boot的常用关键注解

春风十里不如你——掌握Spring Boot的常用关键注解

引言 在Java的世界里&#xff0c;Spring Boot以其简化的配置和开箱即用的特性&#xff0c;成为了构建现代微服务和企业级应用的首选框架。Spring Boot的注解是这一切的核心。在本文中&#xff0c;我们将深入探讨最常用的Spring Boot注解&#xff0c;帮助你轻松驾驭Spring Boot…
阅读更多...
AMEYA360分析兆易创新GD32A490系列车规级MCU

AMEYA360分析兆易创新GD32A490系列车规级MCU

兆易创新GigaDevice今日宣布&#xff0c;正式推出全新GD32A490系列高性能车规级MCU&#xff0c;以高主频、大容量、高集成和高可靠等优势特性紧贴汽车电子开发需求&#xff0c;适用于车窗、雨刷、智能车锁、电动座椅等BCM车身控制系统&#xff0c;以及仪表盘、娱乐影音、中控导…
阅读更多...
2023.12.4 GIT的概念和组成

2023.12.4 GIT的概念和组成

目录 目录 1.git的介绍 2.git的历史 开发者&#xff1a;Linus Torvalds Linux的创始人 3.git和svn的对比 svn:集中式管理 git:分布式管理 4.git管理的组成结构 5.取消git文件夹追踪 1.git的介绍 git是项目版本管理工具,能自动的将多个版本进行管理存储,类似于快照,多个…
阅读更多...
视界臻色彩 轻巧薄未来 《2023年中国OLED电视发展白皮书》发布

视界臻色彩 轻巧薄未来 《2023年中国OLED电视发展白皮书》发布

随着中国经济迈入新周期&#xff0c;彩电行业也进入存量竞争阶段。在此背景下&#xff0c;主流品牌围绕新产品、新技术、新应用等方面积极发力&#xff0c;特别是在高端彩电市场的争夺中&#xff0c;伴随着三星OLED的入局开始变得愈发激烈。我国“十三五”规划中明确指出&#…
阅读更多...
洛雪音乐助手用不了了？使用六音自定义音源即可解决

洛雪音乐助手用不了了？使用六音自定义音源即可解决

用前必读 因为导入的接口源码是直接很明显得可以看到接口地址的&#xff08;跟作者协商处理办法中&#xff09; 为了防止被恶意滥用&#xff0c;所以我加入了接口请求频率限制&#xff0c;3秒内超过5次请求就会封禁IP 所以请务必注意&#xff0c;使用批量下载可能会下着下着就…
阅读更多...
掌汇云 | 全场景数据追踪，多维了解用户偏好，提高运营效率

掌汇云 | 全场景数据追踪，多维了解用户偏好，提高运营效率

掌汇云拥有黄金“三件套”&#xff1a;掌头条、汇互动、云品牌。群硕借助这些功能套件&#xff0c;面向细分领域如&#xff1a;会展&#xff0c;食品饮料、医药以及工业等&#xff0c;定制综合性信息服务平台&#xff0c;提供资讯、商机、企业人脉、上下游资源、活动等高质量服…
阅读更多...
如何在Linux上部署1Panel运维管理面板并远程访问内网Web端管理界面

如何在Linux上部署1Panel运维管理面板并远程访问内网Web端管理界面

文章目录 前言1. Linux 安装1Panel2. 安装cpolar内网穿透3. 配置1Panel公网访问地址4. 公网远程访问1Panel管理界面5. 固定1Panel公网地址 前言 1Panel 是一个现代化、开源的 Linux 服务器运维管理面板。高效管理,通过 Web 端轻松管理 Linux 服务器&#xff0c;包括主机监控、…
阅读更多...
【LeetCode:1038. 从二叉搜索树到更大和树 | BST+DFS+中序遍历】

【LeetCode:1038. 从二叉搜索树到更大和树 | BST+DFS+中序遍历】

&#x1f680; 算法题 &#x1f680; &#x1f332; 算法刷题专栏 | 面试必备算法 | 面试高频算法 &#x1f340; &#x1f332; 越难的东西,越要努力坚持&#xff0c;因为它具有很高的价值&#xff0c;算法就是这样✨ &#x1f332; 作者简介&#xff1a;硕风和炜&#xff0c;…
阅读更多...
我也不想说啊，可这东西行政用能保命啊！

我也不想说啊，可这东西行政用能保命啊！

行政人姐妹在哪里啊&#xff01;在处理工作报告&#xff0c;行政报告等文章的时候&#xff0c;毫无头绪&#xff0c;速度还慢&#xff0c;容易被领导批评。 最近挖到了个抄好用的AI智能写作工具 用它写报告&#xff0c;写总结、写会议记录&#xff0c;写方案等等......写啥都…
阅读更多...
软件开发、管理、运维、实施、验收、交付、安全检查等文档支撑

软件开发、管理、运维、实施、验收、交付、安全检查等文档支撑

软件开发涉及到哪些文档&#xff1a; 全文档获取&#xff1a;点我获取 可行性分析报告&#xff1a;在项目开始前&#xff0c;需要编写可行性分析报告&#xff0c;评估项目的可行性、技术需求、成本预算等因素&#xff0c;为决策提供依据。项目开发计划&#xff1a;明确项目的…
阅读更多...
Java毕业设计—vue+SpringBoot人事管理OA系统前后端分离

Java毕业设计—vue+SpringBoot人事管理OA系统前后端分离

项目介绍 项目背景 人力资源管理是企业运营中必不可少的一环&#xff0c;它关系到企业的前途与发展。尤其对于中小微企业来说&#xff0c;对企业的发展有着举足轻重的作用。随着近年来&#xff0c;政府对创业项目的大力扶持&#xff0c;我国创业型企业蓬勃发展。据统计&#…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023