个人主页:点我进入主页
专栏分类:C语言初阶 C语言程序设计————KTV C语言小游戏 C语言进阶
C语言刷题 数据结构初阶 Linux
欢迎大家点赞,评论,收藏。
一起努力,共赴大厂。
目录
1.前言
2.性质练习
3.代码练习
3.1单值二叉树
3.2检查两颗树是否相同
3.3对称二叉树
3.4另一颗树的子树
4.总结
1.前言
二叉树的学习是枯燥的也是充满乐趣的,它的核心部分是递归,这就需要我们多去刷题,树是一对多的结构,你是否还记得我在上一篇中写到树的内容可以分为根节点,左孩子右孩子,左子树右子树和根节点,左子树右子树这两种方法吗?这两种非常的重要,今天我们的代码部分会让你深刻的了解这句话,没有看上一篇对二叉树的解析的小伙伴可以去我主页进行查找。
2.性质练习
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )
A 不存在这样的二叉树
B 200
C 198
D 199
我们根据二叉树的性质,只要是二叉树就会有度为0的节点个数等于度为2的节点个数加1,所以我们可以得到叶子节点的个数为200个,选择b。
2.下列数据结构中,不适合采用顺序存储结构的是( )
A 非完全二叉树
B 堆
C 队列
D 栈
虽然这几种都可以采用顺序表进行存储,但是非完全二叉树存储起来比较困难,主要是我们不容易找到父节点和孩子节点的位置,所以选择A。
3.在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2
我们知道二叉树有度为0,度为1,度为2,这三种所以我们可以得到n0+n1+n2=2n,我们在根据性质度为0的节点个数等于度为2的节点个数加1得到2n0+n1-1=2n.由于是完全二叉树,所以我们可以知道度为1的节点只能是0或1我们带入后可以知道有一个,所以叶子节点个数为n,所以选择A。
4.一棵完全二叉树的节点数位为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 12
我们根据二叉树的深度为log(n+1),我们可以得到为10,所以选择B。
5.一个具有767个节点的完全二叉树,其叶子节点个数为()
A 383
B 384
C 385
D 386
我们根据最后一个节点编号为766,它的父节点为(766-1)/2=382,所以叶子节点个数为766-382=384.所以我们选择B。
3.代码练习
3.1单值二叉树
965. 单值二叉树
已解答
简单
相关标签
相关企业
如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。
只有给定的树是单值二叉树时,才返回 true;否则返回 false。
示例 1:
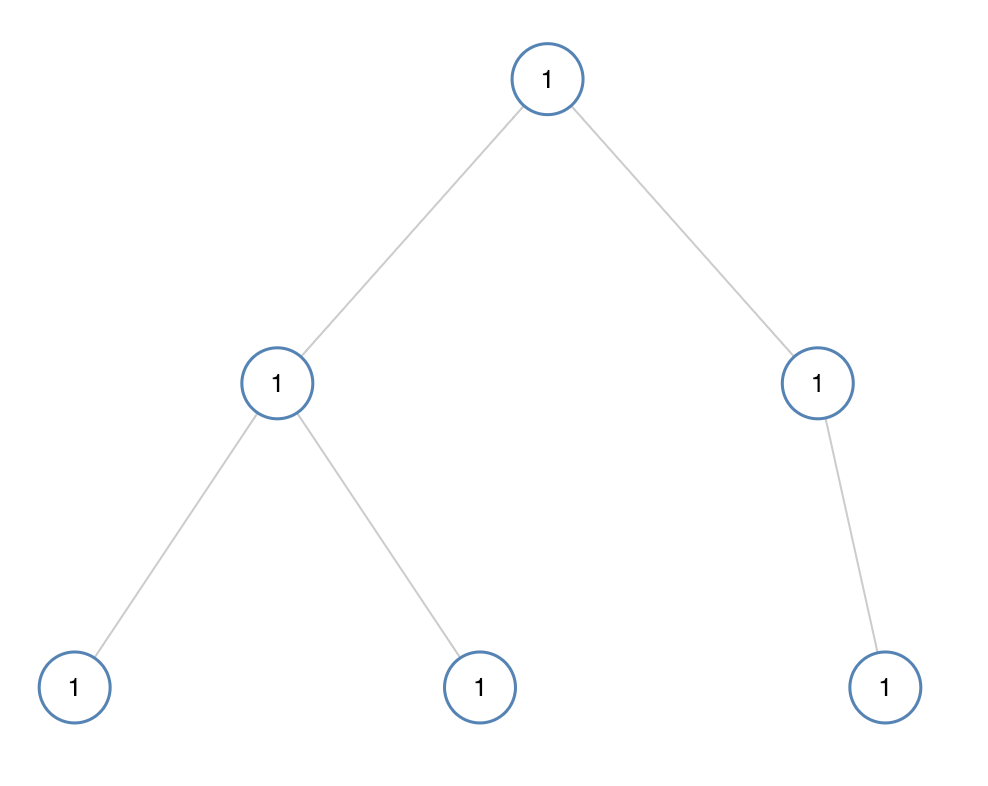
输入:[1,1,1,1,1,null,1] 输出:true
示例 2:
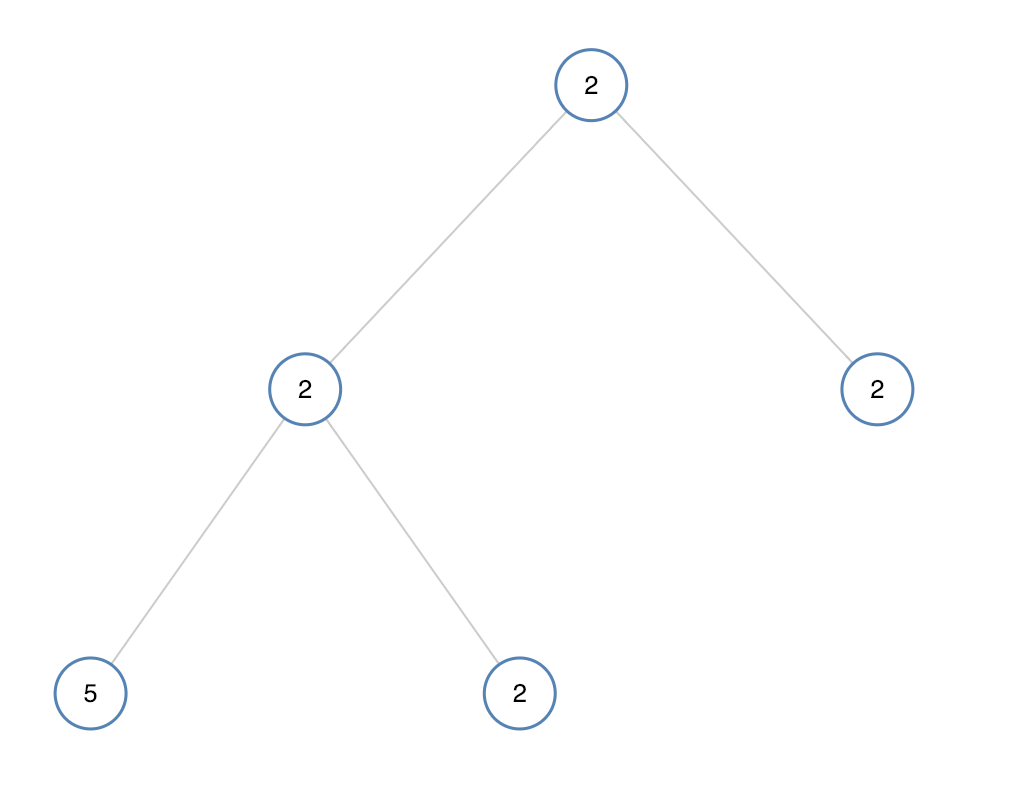
输入:[2,2,2,5,2] 输出:false
在这里我们分为根节点,左孩子右孩子,左子树右子树进行解题,当我们的根节点为空时返回true,当我们的左孩子不为空且值与根节点不同时返回false,当右孩子不为空且值与根节点不同时返回false,然后判断左子树与右子树,代码如下:
bool isUnivalTree(struct TreeNode* root) {
if(root==NULL)
return true;
if(root->left&&root->left->val!=root->val)
return false;
if(root->right&&root->right->val!=root->val)
return false;
return isUnivalTree(root->left)&&isUnivalTree(root->right);
}3.2检查两颗树是否相同
100. 相同的树
已解答
简单
相关标签
相关企业
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
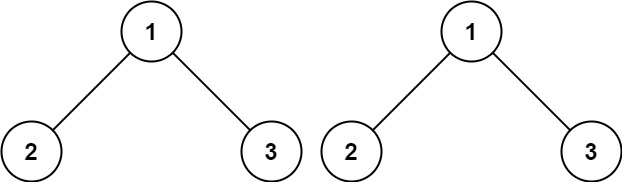
输入:p = [1,2,3], q = [1,2,3] 输出:true
示例 2:
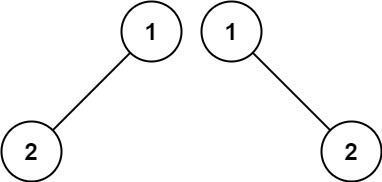
输入:p = [1,2], q = [1,null,2] 输出:false
示例 3:
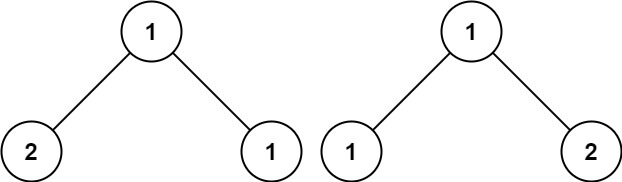
输入:p = [1,2,1], q = [1,1,2] 输出:false
在这里我们分为根节点,左子树右子树,当我们的根节点都为空时返回true,当其中一个为空,另一个不为空时返回false,当都不为空时值不相同返回false,然后在判断左子树和右子树,详细代码如下:
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
if(p==NULL&&q==NULL)
return true;
if(p==NULL&&q!=NULL)
return false;
if(p!=NULL&&q==NULL)
return false;
if(p->val!=q->val)
return false;
return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}3.3对称二叉树
101. 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
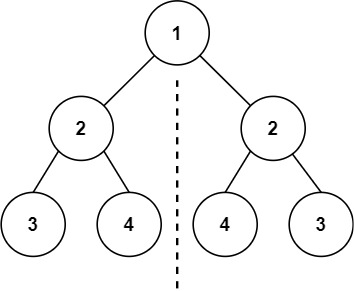
输入:root = [1,2,2,3,4,4,3] 输出:true
示例 2:
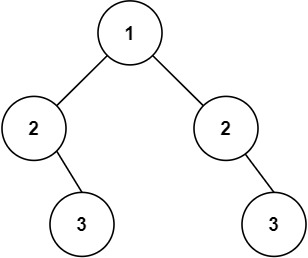
输入:root = [1,2,2,null,3,null,3] 输出:false
我们根据根节点,左孩子右孩子,左子树右子树进行判断,我们先判断根节点是否为空,为空返回false,然后判断左孩子和右孩子是否相同,然后返回左子树和右子树,这时候我们就将问题转化为判断左子树和右子树是否是同一颗树,我们就将问题转化为根节点,左子树右子树的问题,先判断权为空返回true,一个为空另一个不为空返回false,都不是空但是值不相同反水false,然后反水左子树与右子树。详细代码如下:
bool mysymmentric(struct TreeNode* p,struct TreeNode* q)
{
if(p==NULL&&q==NULL)
return true;
if(p&&q&&q->val!=p->val)
return false;
if(p==NULL&&q!=NULL)
return false;
if(p!=NULL&&q==NULL)
return false;
return mysymmentric(p->right,q->left)&&mysymmentric(p->left,q->right);
}
bool isSymmetric(struct TreeNode* root) {
if(root==NULL)
return true;
if(root->left==NULL&&root->right!=NULL)
return false;
if(root->right==NULL&&root->left!=NULL)
return false;
return mysymmentric(root->left,root->right);
}3.4另一颗树的子树
572. 另一棵树的子树
已解答
简单
相关标签
相关企业
提示
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
示例 1:
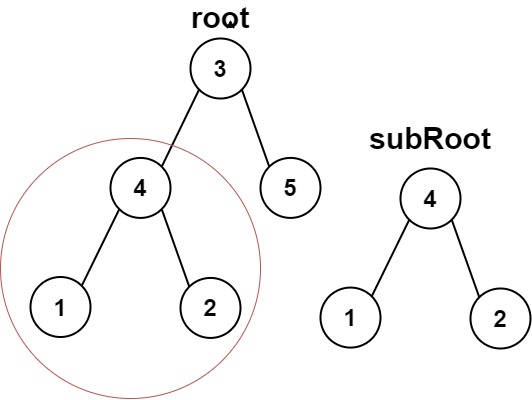
输入:root = [3,4,5,1,2], subRoot = [4,1,2] 输出:true
示例 2:
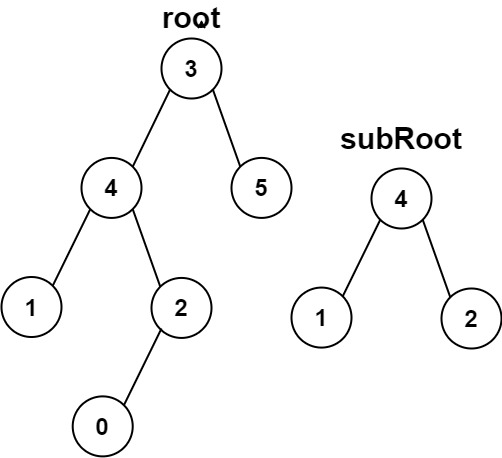
输入:root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2] 输出:false
我们同样将问题转化为根节点,左子树右子树,当根结点为空时返回false,当根节点的值与它相同时进行判断是不是为相同的树,这是时候我们还是根节点,左子树右子树进行判断,当都为空时返回true,只有一个为空时返回fasle,值不相同时返回false,然后进行判断左子树右子树。然后判断左子树与右子树。详细代码如下:
bool issampetree(struct TreeNode* root1,struct TreeNode* root2)
{
if(root1==NULL&&root2==NULL)
return true;
if(root1==NULL&&root2!=NULL)
return false;
if(root2==NULL&&root1!=NULL)
return false;
if(root1->val!=root2->val)
return false;
return issampetree(root1->right,root2->right)&&issampetree(root1->left,root2->left);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
if(root==NULL)
return false;
if(root->val==subRoot->val)
{
if(issampetree(root,subRoot))
return true;
}
return isSubtree(root->right,subRoot)||isSubtree(root->left,subRoot);
}4.总结
今天的内容就到这里了,想要学好二叉树就需要多练,可以多看看这篇文章和上一篇二叉树的文章,相信大家可以学到很多,其实二叉树就是递归,多画几次递归展开图就能理解其中是如何运行的。最后别忘了三连呀。


![smarty模版 [BJDCTF2020]The mystery of ip 1](https://img-blog.csdnimg.cn/direct/5c47cf3c7aab4eb2a6e48c537626ea04.png)