君兮_的个人主页

即使走的再远，也勿忘启程时的初心

C/C++ 游戏开发

Hello,米娜桑们，这里是君兮_，博主最近一直在钻研动态规划算法，最近在Leetcode上刷题的时候遇到一个Hard难度的动态规划题，今天就借此机会来给大家分享一下我对这个题目的一些看法和解题思路（放心，我是AC了的）

• 好了废话不多说，开始我们今天的学习吧！！

地下城游戏

• Leetcode上的原题链接在这里：地下城游戏

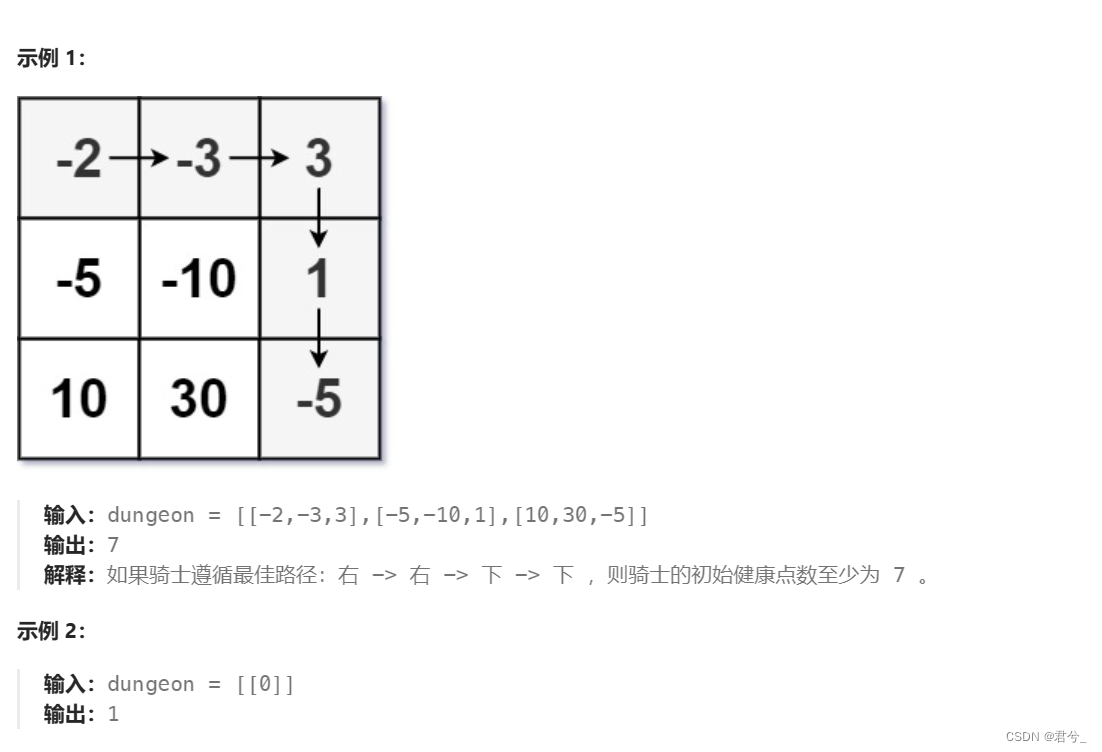
• 好好好，一看题目里一大堆字还看不懂它到底什么意思，再看看上面标的hard难度，一大堆人相信和博主一样上来就准备先点击退出了，大家先不要捉急，我来带大家一步一步分析一下这个题目的意思

题目解析

（ps：这个在漫画里真是公主）

• 我们的公主被抓住关在了最右下角，如图所示
  
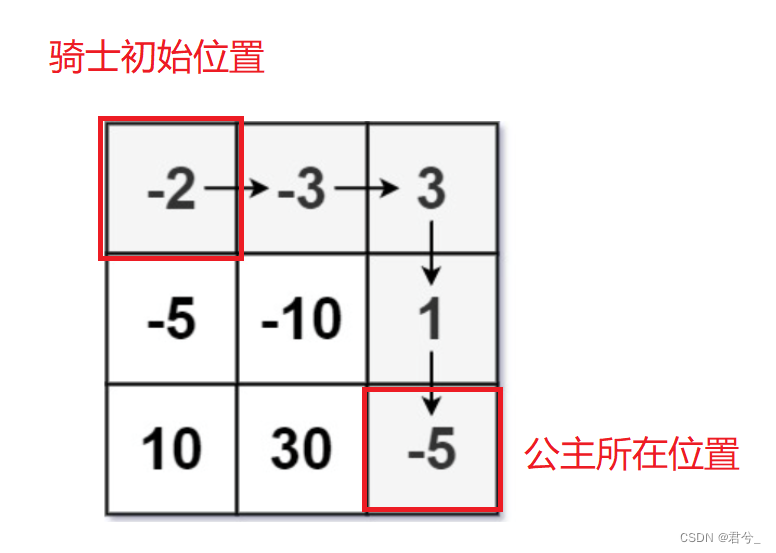
• 接下来，我们的骑士要从图中位置出发，其中遇到恶魔（也就是格子里的值为负值）就需要与它们战斗会扣血，当遇到魔法球（图中为正值），就可以回血。此时，题目问我们，在初始位置时，骑士至少需要多少血（规定当在某个位置血量大于等于1即可通过否则失败）
• 那么，通过题目的描述，结合之前我们学过的动态规划思想，你发现什么不一样了吗？作为Hard难度的题，想用常规的思维来解决肯定是不可能的，好了，接下来我带大家具体分析一下其中的算法原理吧

---

算法原理

1. 状态表示

• 我们之前在动态规划的算法中说过，遇到动态规划问题时，一般的解决方式就是分两种情况：
• • （1） 选择某一个位置为终点结束，建立dp表，进行状态表示
• • （2）选择某一个位置为起点出发…
• 按照常规思路，我们既然知道了公主的位置，那正常情况就是选择第一种情况来试着进行状态表示
• 这道题如果我们照着这个思路定义成：从起点开始，到达[i, j] 位置的时候，所需的最低初始健康点数。
• 那么我们分析状态转移的时候会有⼀个问题：那就是我们当前的健康点数还会受到后面的路径的影响。也就是从上往下的状态转移不能很好地解决问题。

这里是为什么呢？我们设想一下，假设此时我们骑士的血很少，下一格无论是朝下还是朝右都会遇到恶魔把我们骑士的血扣为负数，那此时这里的dp值合理吗？很显然是不合理的。因此我们出了考虑前面位置的情况，还要考虑后面路径的情况，岂不是太麻烦了？

• 这个时候我们要换⼀种状态表示：从[i, j] 位置出发，到达终点时所需要的最低初始健康点数。这样我们在分析状态转移的时候，前面的路径不需要考虑，后续的最佳状态已经知晓，这样就极大的简化了我们分析的难度。

• 综上所述，定义状态表示为：
  dp[i][j] 表示：从[i, j] 位置出发，到达终点时所需的最低初始健康点数

---

2 状态转移方程

• 对于 dp[i][j] ，从 [i, j] 位置出发，下⼀步会有两种选择（为了方便理解，设 dp[i][j] 的最终答案是 x）：

• i. ⾛到右边，然后⾛向终点

• 那么我们在 [i, j] 位置的最低健康点数加上这⼀个位置的消耗，应该要⼤于等于右边位置的最低健康点数，也就是： x + dungeon[i][j] >= dp[i][j + 1] 。
  通过移项可得： x >= dp[i][j + 1] - dungeon[i][j] 。因为我们要的是最⼩值，因此这种情况下的 x = dp[i][j + 1] - dungeon[i][j] ；

• ii. ⾛到下边，然后⾛向终点

• 那么我们在 [i, j] 位置的最低健康点数加上这⼀个位置的消耗，应该要⼤于等于下边位置的最低健康点数，也就是： x + dungeon[i][j] >= dp[i + 1][j] 。
  通过移项可得： x >= dp[i + 1][j] - dungeon[i][j] 。因为我们要的是最⼩值，因此这种情况下的 x = dp[i + 1][j] - dungeon[i][j] ；

• 综上所述，我们需要的是两种情况下的最⼩值，因此可得状态转移⽅程为：
  dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j]

• 但是，如果当前位置的 dungeon[i][j] 是⼀个⽐较⼤的正数的话， dp[i][j] 的值可能变成 0 或者负数。也就是最低点数会⼩于 1 ，那么骑⼠就会死亡。因此我们求出来的 dp[i][j] 如果⼩于等于 0 的话，说明此时的最低初始值应该为 1 。处理这种情况仅需让 dp[i][j] 与 1 取⼀个最⼤值即可：
  dp[i][j] = max(1, dp[i][j])

什么意思呢？就是这里的[i,j]会给恢复一大口血，但是如果此时的dp[i,j]为负数的时候，说明此时这里要求的骑士的最低血量是0或者负数，这显然是不符合要求的，因此我们需要对这种特殊情况进行一下上述的这种处理

初始化

• 可以在最前⾯加上⼀个「辅助结点」，帮助我们初始化。使⽤这种技巧要注意两个点：
• i. 辅助结点⾥⾯的值要「保证后续填表是正确的」；
• ii. 「下标的映射关系」。

有关辅助节点的使用方法在上面链接的博客中讲过了，这里就不再详叙

• 在本题中，由于我们要考虑后面路径对现在位置的影响，需要在dp表最后面添加一行，并且添加⼀列后，所有的值都先初始化为无穷大，然后让dp[m][n - 1] 或dp[m - 1][n] = 1 即可。

填表顺序

• 根据「状态转移方程」，我们需要「从下往上填每一行」，「每一行从右往左填」。看了上面的算法分析这一点应该不难理解

返回值

• 从题目中可知，我们的骑士是从左上角开始的，因此结合上述分析，我们需要返回的值为dp[0][0]

---

编写代码

class Solution {
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) {
        int m=dungeon.size();
        int n=dungeon[0].size();
        //建立dp表，以某个位置为开始建立状态转移方程
        vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));
        dp[m][n-1]=1;//考虑边界问题
        for(int i=m-1;i>=0;i--)
        {
            for(int j=n-1;j>=0;j--)
            {
            	//填表
                dp[i][j]=min(dp[i+1][j],dp[i][j+1])-dungeon[i][j];
                dp[i][j]=max(1,dp[i][j]);
            }
        }
        //返回值
        return dp[0][0];

    }
};

• 代码很简单，只有十几行，实际上难的是上面分析题目的过程以及对一些特殊情况的判断，代码这里相信如果你能看懂上述原理的分析，这点对你来说应该一点都不难。

---

总结

• 好啦，我们今天的内容就先到这里啦！其实代码并不重要，能看懂背后隐藏的原理并且通过这个题目学会对应题目的分析才重要，因此如果你想真正学会的话，不妨自己从头试着理解一下算法原理再自己独立编写代码，这样我相信是最能提升自己有关动态规划题目的理解的。
• 有任何的问题和对文章内容的疑惑欢迎在评论区中提出，当然也可以私信我，我会在第一时间回复的！！

新人博主创作不易，如果感觉文章内容对你有所帮助的话不妨三连一下再走呗。你们的支持就是我更新的动力！！！

**（可莉请求你们三连支持一下博主！！！点击下方评论点赞收藏帮帮可莉吧）**