这篇文章讲介绍：同余方程，中国剩余定理

什么是同余方程？

x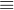y （mod p）这样的，带同余号的式子就是同余方程。

什么是中国剩余定理？

中国剩余定理，顾名思义是出自中国，它最早在《孙子算经》中出现，就是为了解决一类一元一次线性同余方程。

举个例子：

有一个数，对3取模为2，对5取模为3，对7取模为2 ， 求这个数

写成同余方程就是：
1：x ==2（mod 3）
2：x ==2（mod 5）
3：x ==2（mod 7）
我们需要去解这个同余方程组。
就需要用到中国剩余定理（具体证明可以自查，这里只给出结论）

1：x ==a1（mod m1）
2：x ==a2（mod m2）
3：x ==a3（mod m3）
.....
n:  x == an ( mod mn )

其中m1,m2,m3......mn两两互质
第一步：设M=m1*m2*m3*.......mn =

第二步：设 bi = M / mi (整除）

第三步：设 inv(bi) bi^-1 (mod mi)   (不是bi的倒数，是bi模mi的逆元）

利用  bi * inv（bi）  1 （mod mi） 求出 inv（i）

我们就可以得到x的通解：
第四步：x= a1*b1*t1 + a2*b2*t2+…… an*bn*tn + kM = ;

代入上面的例子我们可以得到：x=23+k*105；

所以我们需要分成 四步来求，
第一步：累乘模数  M=m1*m2*……mn；
第二步：累乘结果除以对应模数： bi = M/mi
第三步：求bi模以mi的逆元 inv（bi） （用费马小定理，或exgcd）
第四步：求和    （余数*逆元*（模数之积/模数）） + k模数之积

也就是 x = [从i=0到i=n累加]：（ ai*inv（bi）*bi ）+ kM，

所以我们就求出了x的通式子，我们要算出最小正整数x应该咋办捏，就直接+M 在对M取模就行了嗷嗷嗷。
x=（x+M）%M；
 

洛谷P1495 曹冲养猪

设其一共有x只母猪。
已知数据：(为了套板子，直接把数组名换成熟悉的）
猪圈数：m1，m2，m3，m4……mn
剩余猪：a1，a2，a3，a4……an

也就是猪圈就是模数，剩余猪就是余数。
也就有同余方程组：

x==a1 （mod m1）
x==a2 （mod m2）
………………
x==an（mod mn）

接下来用中国剩余定理套板子即可：

第一步：求模数之积：M = m1*m2*m3……mn
第二步：求模数之积除以当前模数：bi=M/mi
第三步：求bi模以mi逆元inv（bi）：

如何用exgcd求inv（bi）
下面推公式：
bi*inv（bi） = 1 （mod mi）
bi*inv（bi）+ y*mi = 1
exgcd（bi，mi，&inv（bi），&y）即可
数据保证 bi 与 mi 互质

第四步：求和
x = （求和）ai*bi*inv（bi）+kM
由于我们要求的是最小正整数的x，所以直接套公式：
x=（x+ai*bi*inv（bi）+M）%M；
x=（x%M+ai*bi*inv（bi）%M +M）%M；

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<cstring>
#include<string>
#include<algorithm>
#include<vector>
#include<cctype>
#include<map>
#include<set>
#include<queue>
#include<numeric>
#include<iomanip>
using namespace std;
typedef long long LL;
const int N = 20;


void exgcd(int a, int b, int &x, int &y) {
	if (b == 0) {
		x = 1, y = 0;
		return;
	}
	exgcd(b, a % b, y, x);
	y -= a / b * x;
}
LL M = 1;
int inv[N], a[N], m[N];
LL b[N];
int t;
int main() {
	int n;
	cin >> n;
	
	for (int i = 1; i <= n; i++) {
		cin >> m[i] >> a[i]; // m为模数，a为余数
		M *= m[i]; // 求模数之积
	}
	LL x = 0;
	for (int i = 1; i <= n; i++) {//求模数之积除以当前模数
		b[i] = M / m[i];
	
		exgcd(b[i], m[i], inv[i], t);
		inv[i] = (m[i] + inv[i]) % m[i];
		 
		while (a[i]--) {
			x = (x + inv[i] * b[i])%M;
		}
	}
	cout << x;

}