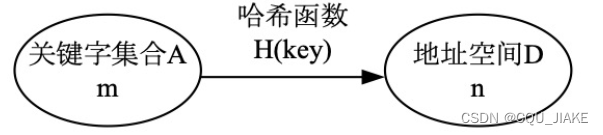
散列函数定义

 

 

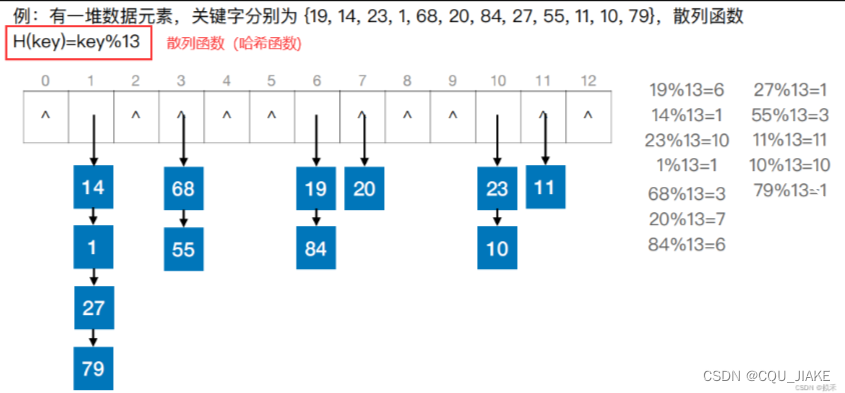
ASL计算 

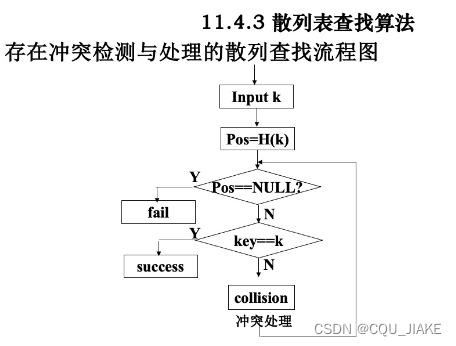
查找长度——在查找运算中，需要对比关键字的次数称为查找长度（有的教材也会把“空指针”的判定算作一次比较）

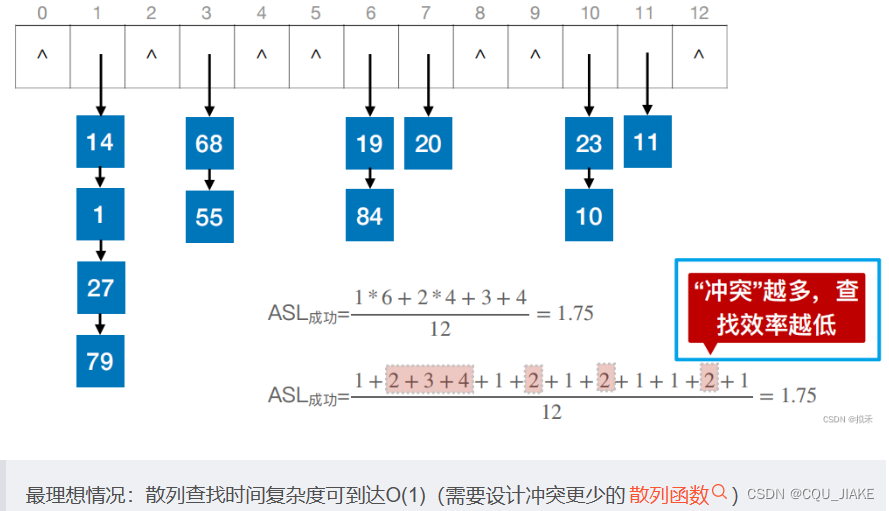
14，68，19，20，23，11这6个元素查一次就可以；1，55，84，10需要查两次；27要3次，79要4次

装填因子

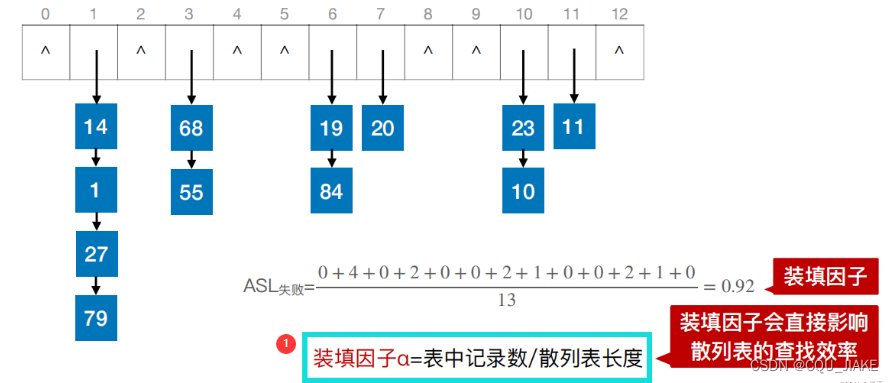
表中记录数就是每个格子里放的数

散列函数

输入指定的元素，输出一个该元素对应的哈希值

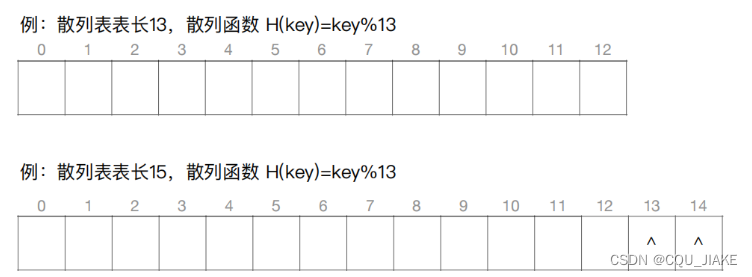
例

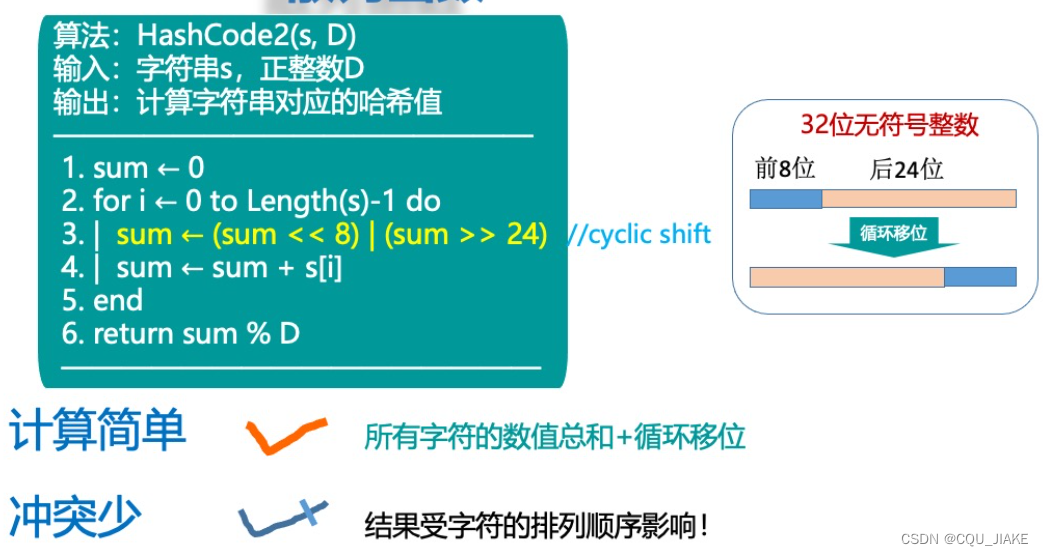
没有考虑次序问题，即同字符不同排序会对应同一哈希值造成冲突

除留余数法

直接定址法

 数字分析法

 

 

所谓分布均匀就是这位上所有数字都有可能出现，不均匀就是这位上更偏向于出现某一特定的值

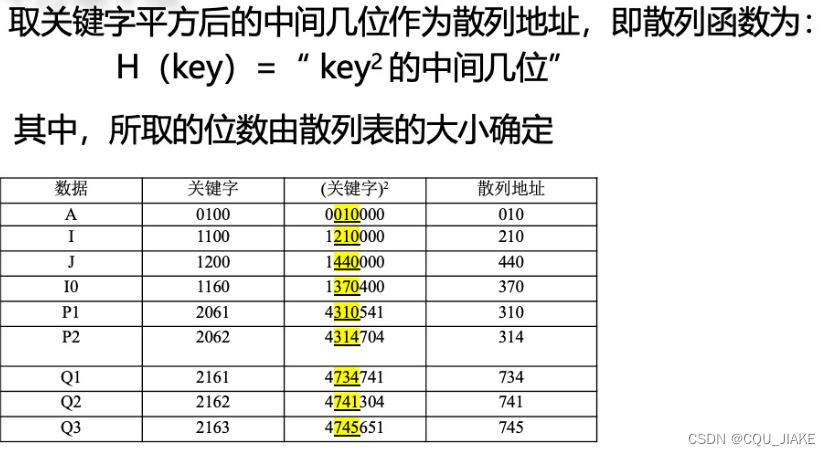
平方取中法

折叠法

移位叠加就是每行从模的开始开始；边界叠加就是一条龙连续的下来

随机数法

开放定址法

开放定址就是冲突处理的一种方式

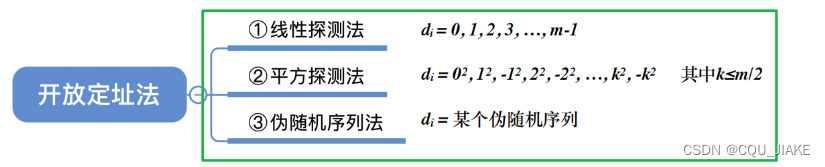
线性探测法

就是令d=1,2,3……,不断往后尝试

但是会造成聚集，即随着存储元素的增多，存储元素会冲突，而且堆积在一起，即这里冲突了，下一个也会冲突，不断冲突，直到出了聚集区域，但挨着聚集区域存储，又相当于增添了聚集区域大小。

• 线性探测法很容易造成同义词、非同义词的“聚集(堆积)”现象，严重影响查找效率
• 产生原因——冲突后再探测一定是放在某个连续的位置

 平方探测法

和线性相比，主要就是d的确定不一样。

散列表长度 m 必须是⼀个可以表示成 4j + 3 的素数，才能探测到所有位置

”截断查找路径“

当在哈希表中进行查找时，如果遇到已删除的元素，线性探测法会继续向后探测，寻找下一个非空槽。如果置为空，这就导致了“截断”同义词结点的查找路径的情况。

索引	元素
0	12
1	23
2	34
3	45
4	56
5	67
6	78
7	89
8	90
9	101

现在需要删除元素56，为了保持哈希表的正确性，采用懒删除的方式。删除后，哈希表的状态如下：

索引	元素
0	12
1	23
2	34
3	45
4	已删除
5	67
6	78
7	89
8	90
9	101

就是说，如果查找的元素冲突了，往后接着找。

在删除路径上某一元素后时，如果直接标记为空，就会不再继续往后探测，而是认为后面都是空的，但实际上空的后面是存储着元素的，所以这个”空“就截断了继续向后的查找路径，即后面可能有要操作的元素，但因为这个”空“认为没有，就会导致再在空里插入相同的元素。所以就需要区分”空“与”已删除“

在查找时，遇到”已删除“则继续进行查找，遇到”空“则表明查找失败。

在插入新节点时可以在”已删除“的节点上进行操作

理解

为什么需要哈希函数？不就是为了得到唯一的哈希值，直接编号不就是吗？

哈希值在内存中通常不是连续存储的，而是通过哈希表来进行存储。哈希表是一种基于数组和链表的数据结构，用于实现高效的插入、查找和删除操作。

哈希表由一个数组和一组哈希桶组成。数组的每个元素称为哈希桶，每个哈希桶可以存储一个或多个元素。哈希函数将输入数据映射到哈希桶的索引位置，然后将元素存储在对应的哈希桶中。

当需要存储一个元素时，首先通过哈希函数计算得到该元素的哈希值，然后根据哈希值找到对应的哈希桶。如果哈希桶为空，则将元素直接存储在该桶中；如果哈希桶已经包含了其他元素，通常会使用链表或其他数据结构将新元素链接到已有元素的后面。

当需要查找一个元素时，同样先通过哈希函数计算得到该元素的哈希值，然后根据哈希值找到对应的哈希桶。如果哈希桶为空，则表示没有找到该元素；如果哈希桶不为空，则需要在哈希桶的链表或其他数据结构中顺序查找，直到找到目标元素或到达链表末尾。

通过哈希表的这种方式，可以在平均情况下实现常数时间的插入、查找和删除操作。当然，在极端情况下，哈希冲突可能会导致链表过长，从而影响性能。为了保持哈希表的高效性，通常会对哈希表进行动态扩容，并使用一些解决冲突的方法，如链地址法或开放寻址法。这样可以保证哈希表的负载因子较低，减少冲突的发生。

数组可以认为是一种哈希表，它的哈希值是连续的，哈希桶也是连续的。

散列查找

例子：线性

查找性能：

查找效率取决于散列函数、处理冲突的方法、装填因子α

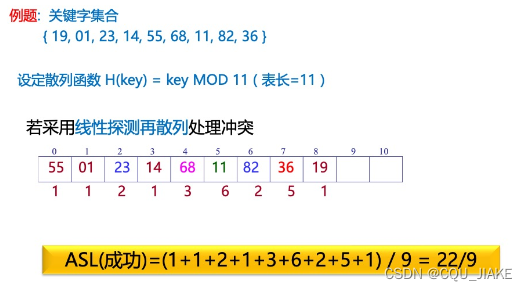
23mod11=1,68Mode11=2.和每个格子的比较都需要一次查找次数。

查找失败的条件为，对应哈希值的位置为”空“，则表明查找失败。 遇到”已删除“则继续进行查找

如果计算出的哈希值对应的结点直接是空，那么直接失败（如9，10）；

如果对应的结点值不是需要的，那么进行冲突处理，如果就是没有，那就继续进行到空结点的位置（这里线性探测，所以就是连续到9的位置，一共11个元素，那么9和10是1次，和自己判断需要一次，然后0~8要不断和自己比较，比较后往后走一步）。

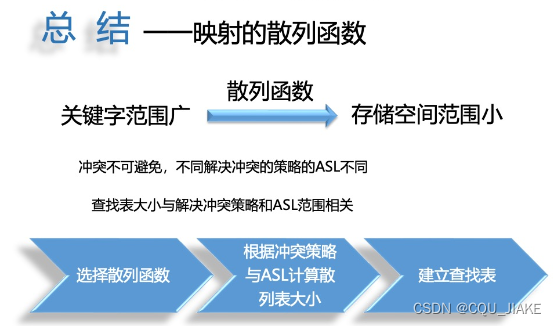
总结图