一、枚举算法
枚举算法,将问题的所有可能的情况进行逐一列举,然后筛选出符合要求的一种程序处理算法。
枚举算法(特别是暴力枚举的时候)的缺点是,容易超时。一个计算机一般 1 秒最多运行 1e8 次,一旦超过 1e8 组数据,就有可能超时。
枚举三要素:
1. 枚举对象(要枚举的对象)
2. 枚举范围(每一个枚举对象从几开始,到几结束)
3. 筛选条件(筛选满足一定条件的数据)
二、最大公约数
约数:如果一个整数 a 能被整数 b 整除,那么 b 就是 a 的约数。
公约数:两个或者多个数公有的约数。
计算两个整数 a 和 b 的最大公约数,如何利用程序实现?
1. 枚举对象:1 个数 x(可能是最大公约数的数)
2. 枚举范围:1 <= x <= min(a, b)
3. 筛选条件:如果 a % x 是 0 ,并且 b % x 也是 0 。
建议倒序遍历。
根据上述思路,我们写出代码:
#include <iostream>
using namespace std;
int main()
{
// 输入两个数字
int a, b;
cin >> a >> b;
// 枚举算法
int minn = min(a, b);
for (int i = minn; i >= 1; i--)
{
if (a % i == 0 && b % i == 0)
{
cout << i;
break;
}
}
return 0;
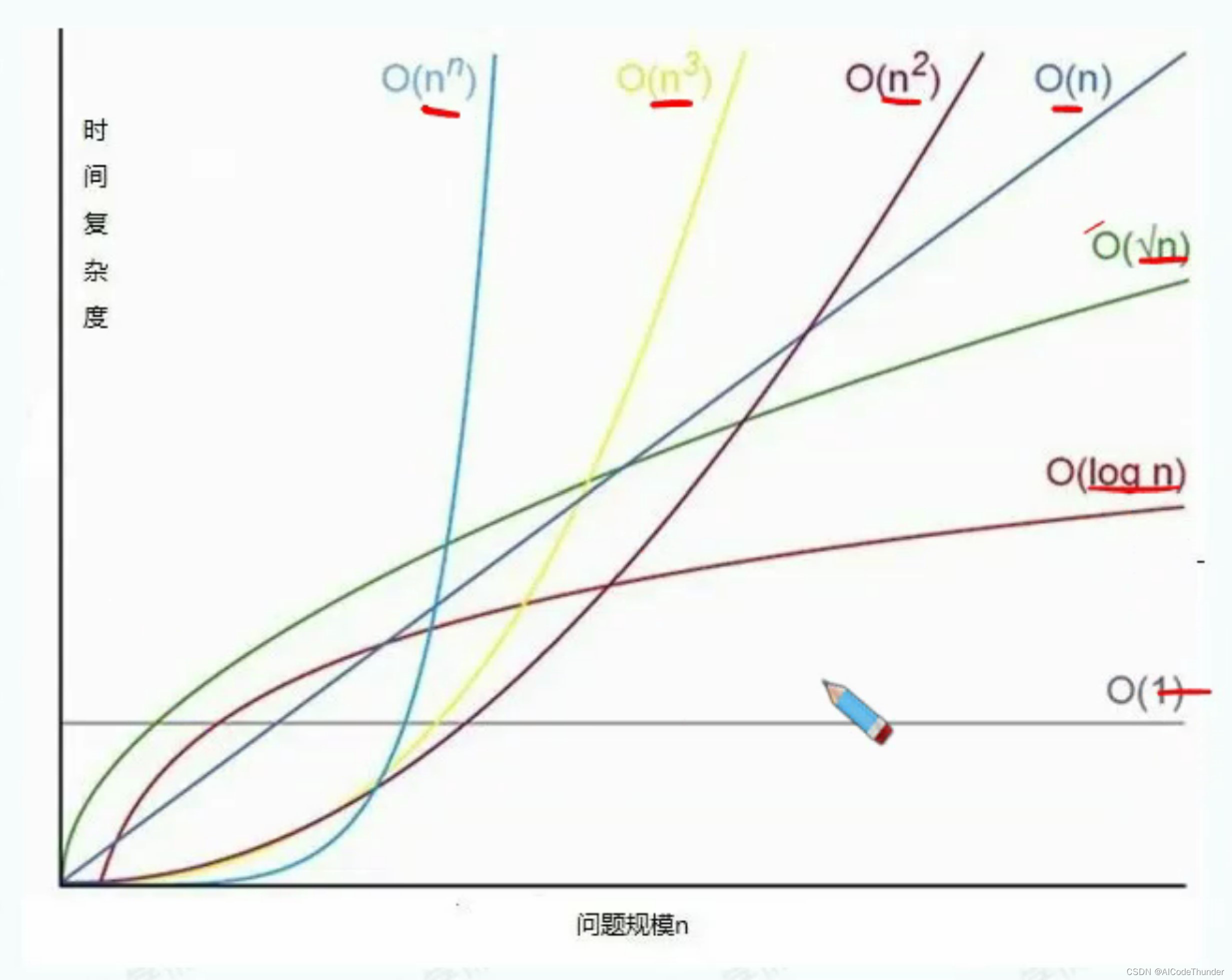
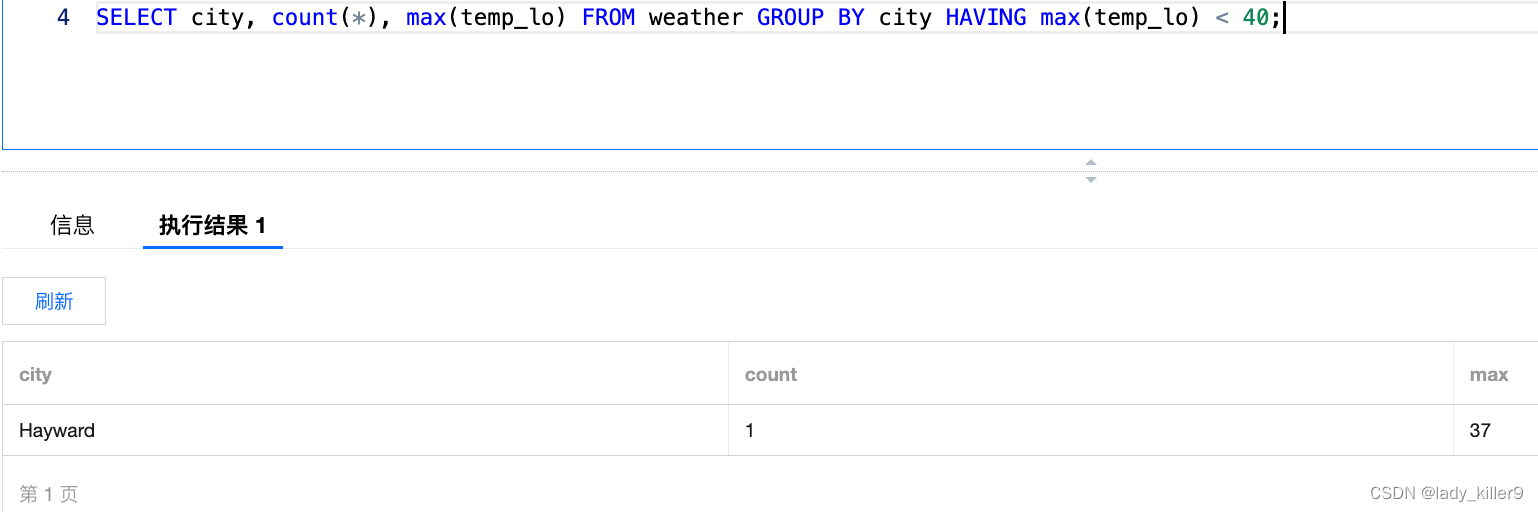
}时间复杂度O(n),概念图如下:
测试结果:
于是,我们还需要继续……嗯,现在教大家一种方法——辗转相除法,用了就无敌了!
将除数 b 当作下一次的被除数,余数 r 当作下一次的除数。如此反复地进行,一旦余数是 0 ,最后余数是 0 算式的除数。
比如说 63 ÷ 24。
63 ÷ 24 = 余15
24 ÷ 15 = 余9
15 ÷ 9 = 余6
9 ÷ 6 = 余3
6 ÷ 3 = 余0
所以 63 和 24 的最大公约数是 3 。
辗转相除法程序逻辑:
int a, b, r;
while (a % b)
{
r = a % b; // 得到余数
a = b; // 除数作为下一次的被除数
b = r; // 余数作为下一次的除数
}
cout << b;是的,这样就 OK 啦。
三、最小公倍数
1. 枚举对象:1 个数 y(可能是最小公倍数的数)
2. 枚举范围:max(a, b) <= y <= a × b
3. 筛选条件:如果 y % a 是 0 ,并且 y % b 也是 0 。
建议正序遍历。
#include <iostream>
using namespace std;
int main()
{
// 输入
int a, b;
cin >> a >> b;
// 枚举算法
int maxn = max(a, b);
for (int i = maxn; i <= a*b; i++)
{
if (i % a == 0 && i % b == 0)
{
cout << i;
break;
}
}
return 0;
}拓展一个特殊关系:
整数 a × 整数 b = 最大公约数 × 最小公倍数
#include <iostream>
using namespace std;
int main()
{
// 输入
long long a, b;
cin >> a >> b;
long long olda = a, oldb = b;
// 枚举算法
int r;
while (a % b)
{
r = a % b;
a = b;
b = r;
}
cout << olda*oldb/b;
return 0;
} 这样,其实我们最小公倍数用的就是公式,大部分都是最大公约数的程序。
四、真题
题目描述
输入两个正整数x0,y0(2<=x0<100000,2<=y0<=100000),求出满足下列条件的P,Q的个数
条件:
1.P,Q是正整数
2.要求P,Q以x0为最大公约数,以y0为最小公倍数.
试求:满足条件的所有可能的两个正整数的个数.
输入描述
输入二个正整数x0,y0(2<=x0<100000,2<=y0<=100000)
输出描述
输出满足条件的P,Q的个数。
样例1
输入
3 60输出
4
提示
说明(不用输出)此时的P Q分别为:
3 60
15 12
12 15
60 3
所以:满足条件的所有可能的两个正整数的个数共4种.
解题思路
1. 枚举对象:p ( q 可以通过 x × y ÷ p 得到)
2. 枚举范围:x <= p <= y
3. 筛选条件:如果 p 和最大公约数 x 相等
参考代码
#include <iostream>
using namespace std;
int main()
{
// 输入
long long x, y;
cin >> x >> y;
// 枚举算法
long long p, q, cnt = 0;
for (int i = x; i <= y; i++)
{
p = i;
q = x*y/p;
if (x * y % p == 0)
{
// 寻找 p 和 q 的最大公约数,得到最大公约数 q
while (p % q)
{
r = p % q;
p = q;
q = r;
}
if (q == x)
{
cnt++;
}
}
}
// 输出所有可能
cout << cnt;
return 0;
}