基于Logistic回归实现二分类

news2025/1/12 17:57:00

Logistic回归公式推导：

Sigmoid函数：

Logistic回归如何实现分类：

优化的方法：

代码：

1.创建一个随机数据集，分类直线为y=2x：

为什么用np.hstack()增加一列1？

为什么返回值设成三个？

为什么预先设置分类直线? 因为全随机的点数太难以确定：

2.梯度上升算法实现：

为什么使用train_y=np.array(boolean_int(y)).reshape(100,1)？

X[y==0,0],X[y==0,1]是什么东西？

疑问：

Logistic回归公式推导：

(系列四) 线性分类5-逻辑回归（Logistic Regression）_哔哩哔哩_bilibili

回归：

存在一系列数据点，使用一条直线对这些点进行拟合，拟合的过程即为回归。

线性回归:

线性回归方程如下：我们输入数据点特征，取合适的w和b，使得预测值y^最接近y。但是我们不能通过方程预测非线性的函数，比如说 $e^{x}$

$y=wx+b$

线性模型的衍生：

$y=g(F(x))=g(wx+b)$

通过这种方式，我们可以拟合非线性函数: 当g(x)取 $e^{x}$ ，得： $y=e^{wx+b}$ , $\ln y = wx+b$

怎么把回归和分类结合起来？

回归方程得到的y的范围是负无穷到正无穷，如何实现分类。以二分类为例，类别分别为0和1，我们需要使用函数将在负无穷到正无穷的数映射到0或1上。我们需要使用Sigmoid函数。

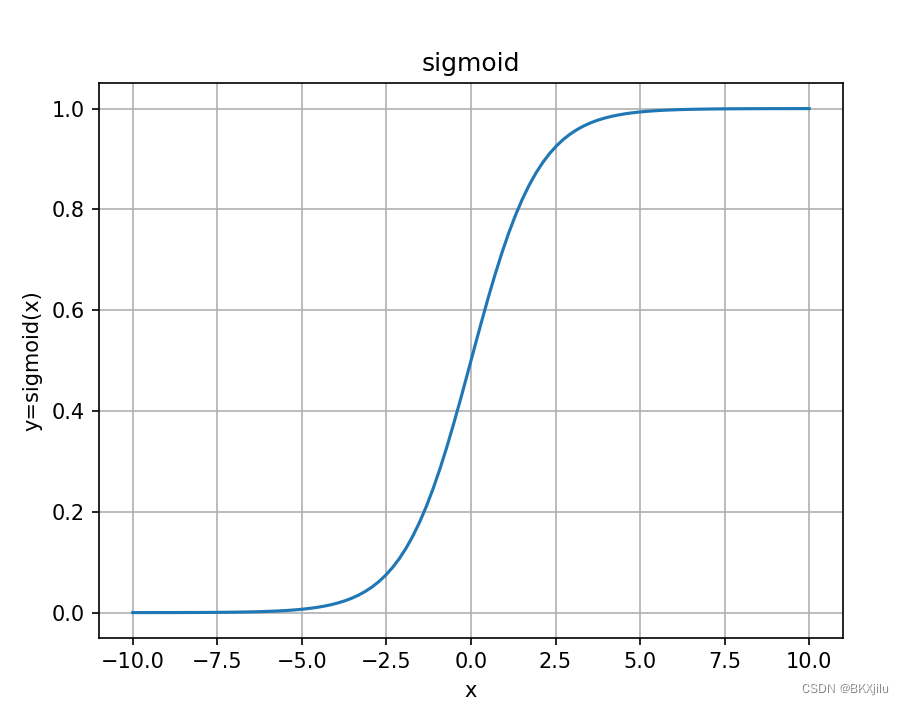
Sigmoid函数：

如图可以发现Sigmoid函数将输入z映射到（0，1）区间，我们可以设置阈值，大于阈值为类别1，小于阈值为类别0.

$\sigma (z)=\frac{1}{1+e^{-z}}$

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1/(1+np.exp(-x))
# np.linspace(start,end,num) 100个数，数在-10，10等距分布
x=np.linspace(-10,10,100)
y=sigmoid(x)
plt.plot(x,y)
plt.title("sigmoid")
plt.xlabel('x')
plt.ylabel('y=sigmoid(x)')
#添加网格
plt.grid(True)
plt.show()

Logistic回归如何实现分类：

输入数据点的特征，对每个特征乘以回归系数 $w$ ,然后相加求和得到z,将z作为Sigmoid函数的输入，Sigmoid函数可以将输入映射在0-1区间内，我们将大于0.5部分设置为1类，小于0.5部分设置为0类实现二分类。为了实现更好的分类结果，我们需要对 $w$ 进行优化。

$z=wx+b=w_{1}x1+w_{2}x2+b$

也可以把W和X看成向量，写成如下形式：

$z=w^{\Gamma }x+b$

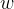优化 $w$ 的方法：

梯度上升方法：a表示学习率， $\bigtriangledown _{w}f(w)$ 表示梯度。

$W = W+a*\bigtriangledown _{w}f(w)$

损失函数：预测y和标签y的差

代码：

1.创建一个随机数据集，分类直线为y=2x：

为什么用np.hstack()增加一列1？

根据： $z=wx+b=w_{1}x1+w_{2}x2+b$ ，

在设计权重时，w1,w2,b都需要通过梯度上升优化，希望可以统一进行梯度计算，但是b不与x相乘，想到： $z=wx+b=w_{1}x1+w_{2}x2+b=w_{1}x1+w_{2}x2+w_{0}x0$ ,

$w_{0}=b$ , $x_{0}=1$

所以在train_x训练集添加一列1，作为x0.

为什么返回值设成三个？

train_X (100x3)包括方便计算的x0,X(100x2)可以用来绘制散点图，train_y表示标签。


def createtraindataset():

    np.random.seed(0)
    n_samples=100
    X=np.random.randn(n_samples,2)
    #featur2>2*feature1时 y为true，否则y为false
    y=(X[:,1]>2*X[:,0].astype(int))
    print("y",y)
    new_=np.ones((100,1))
    train_X=np.hstack((new_,X))
    train_y=y
    print("y",train_y)
    return train_X,train_y,X

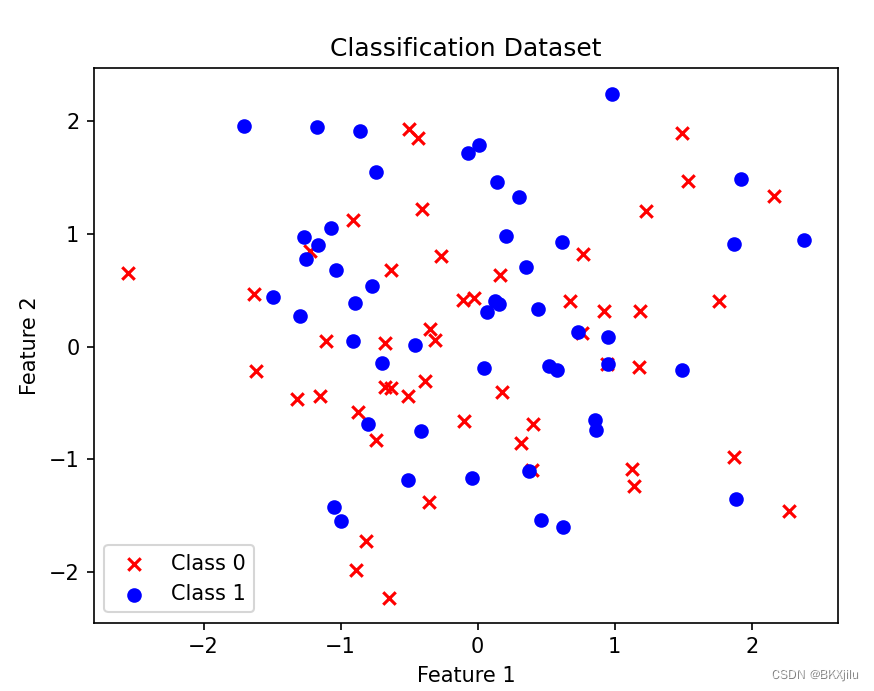
其散点图如图所示 :

其打印出来的y是布尔值，结果如下：

为什么预先设置分类直线? 因为全随机的点数太难以确定：

    n_samples=100
    X=np.random.randn(n_samples,2)
    y=np.random.randint(2,size=100)

散点图：根本没办法进行划分。

2.梯度上升算法实现：

为什么使用train_y=np.array(boolean_int(y)).reshape(100,1)？

def boolean_int(y):
    return [1 if cell else 0 for cell in  y]

如上boolean_int 把布尔y转化为int型y,并reshape到（100，1）避免出现维度不匹配问题。

y.shape为（100，）->train_y.shape(100,1)

X[y==0,0],X[y==0,1]是什么东西？

y是布尔值，numpy可以使用布尔值进行索引：

numpy 布尔索引的用法-CSDN博客

def test():
    y=[1,0,1,1]
    np.random.seed(0)
    n_samples=5
    x=np.random.randn(n_samples,2)
    y=np.random.randint(2,size=5)
    print("x=",x)
    print("y=",y)
    print("X[y==0,0]",x[y==0,0],"y==0时对应y数组索引为i,x得到第i行,第0列值")
test()

def grad(train_X,train_y):
    # 100*3
    m,n = len(train_X[:,0]),len(train_X[0])
    #3x1 
    weight=np.ones((n,1))
    #迭代系数
    epoch=500
    for i in range(epoch):
        # mxn nx1 ->m*1
        y_=sigmoid(np.dot(train_X,weight))
        # m*1
        loss = train_y -y_
        a = 0.01
        # 3*1 
        weight = weight - np.dot(a*train_X.transpose(),loss)
    return weight

def plot():
    train_X,y,X=createtraindataset()
    train_y=np.array(boolean_int(y)).reshape(100,1)

    weights=grad(train_X,train_y)
    # weights=weights.getA()
    #100 2*100
    x=np.linspace(-2.5,2.5,5)
    y_=(-weights[0]-weights[1]*x)/weights[2]

    plt.plot(x,y_)    
    plt.scatter(X[y==0,0],X[y==0,1],c='r',marker='x',label='Class 0')
    plt.scatter(X[y==1,0],X[y==1,1],c='b',marker='o',label='Class 1')

    plt.xlabel('Feature 1')
    plt.ylabel('Feature 2')
    plt.legend()
    plt.title("Classification Dataset")
    plt.show()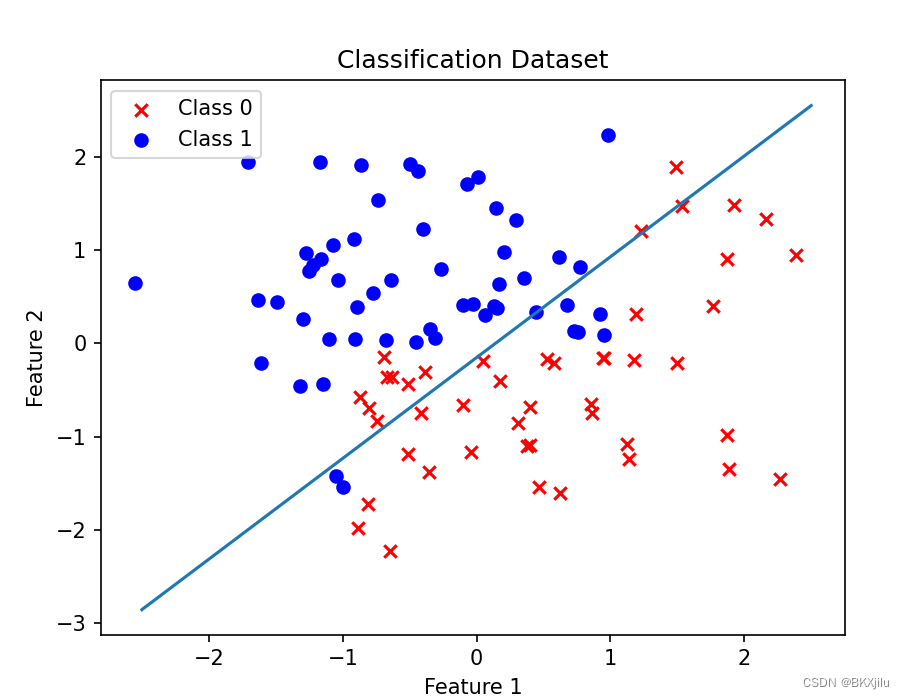

全部代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
def sigmoid(x):
    return 1.0/(1+np.exp(-x))
# # np.linspace(start,end,num) 100个数，数在-10，10等距分布
# x=np.linspace(-10,10,100)
# y=sigmoid(x)
# plt.plot(x,y)
# plt.title("sigmoid")
# plt.xlabel('x')
# plt.ylabel('y=sigmoid(x)')
# #添加网格
# plt.grid(True)
# plt.show()
def boolean_int(y):
    return [1 if cell else 0 for cell in  y]
def createtraindataset():

    np.random.seed(0)
    n_samples=100
    X=np.random.randn(n_samples,2)
    #featur2>2*feature1时 y为1，否则y为0
    y=(X[:,1]>2*X[:,0].astype(int))
    print("y",y)
    new_=np.ones((100,1))
    train_X=np.hstack((new_,X))
    train_y=y
    print("y",train_y)
    return train_X,train_y,X

def grad(train_X,train_y):
    # 100*3
    m,n = len(train_X[:,0]),len(train_X[0])
    #3x1 
    weight=np.ones((n,1))
    #迭代系数
    epoch=500
    for i in range(epoch):
        # mxn nx1 ->m*1
        y_=sigmoid(np.dot(train_X,weight))
        # m*1
        loss = train_y -y_
        a = 0.01
        # 3*1 
        weight = weight - np.dot(a*train_X.transpose(),loss)
    return weight

def plot():
    train_X,y,X=createtraindataset()
    train_y=np.array(boolean_int(y)).reshape(100,1)

    weights=grad(train_X,train_y)
    # weights=weights.getA()
    #100 2*100
    x=np.linspace(-2.5,2.5,5)
    y_=(-weights[0]-weights[1]*x)/weights[2]

    plt.plot(x,y_)    
    plt.scatter(X[y==0,0],X[y==0,1],c='r',marker='x',label='Class 0')
    plt.scatter(X[y==1,0],X[y==1,1],c='b',marker='o',label='Class 1')

    plt.xlabel('Feature 1')
    plt.ylabel('Feature 2')
    plt.legend()
    plt.title("Classification Dataset")
    plt.show()
plot()
# x=np.arange(-2,2,0.1)
# print(len(x))