给定一个数组arr和两个整数a和b求arr中有多少个子数组累加和在a到b这个范围上返回达标的子数组数量
如【3,6,1,9,2】达标的子数组通过暴力求解的方式时间复杂度为O(N的三次方)【找每个子数组占用O(N的二次方)的时间复杂度,然后再算每个子数组的和占用O(N)的时间复杂度总的占用了O(N的三次方的时间复杂度)】
用前缀和的思想可以将时间复杂度降低到O(N的二次方的时间复杂度)
这个题有一个O(N*logN的解法)
分析:假设现在来到i位置,子数组必须以i位置的数结尾达标的有多少个,依次计算,最后求和则得到最终的结果。
假设要求必须以17结尾的子数组范围在[10,60]的有多少个,
假设现在0-17的前缀和是100,假设0-5的前缀和是5,那么可以推出6-17的累加和为95。
那么只要能够找到任何一个前缀和落在[40,90]的范围,那么就能得到以17结尾的子数组落在[10,60]范围。
做法:
有如下数组:
[3,-2,4,3,6,-1] 范围是[1,5]的,假设有一个结构,这个结构是接收前缀和的,那么对于遍历到的当前数x,则需要判断当前数x是否在[1,5]的范围上,以及它的前缀和是否存在落在[sum(x)-5,sum(x)-1]范围上。
那么对于如上数组:
第一步:首先是一个数也没有的时候,我的前缀和结构提前放入一个0,我要整体以0位置结尾落在1-5的范围上,我就在结构中查有多少个前缀和落在[-2,2]上,发现有一个,然后我再将自己的前缀和3扔进前缀和结构
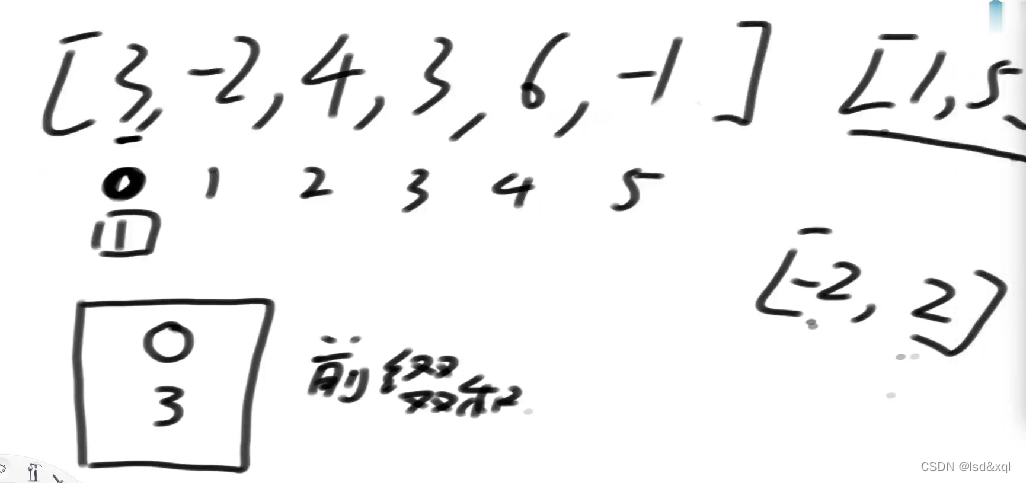
第二步:来到1位置,整体前缀和是1,那么则需要找到在这个前缀和结构中范围落在[-4,0]上面,发现有1个,然后我再将1位置的前缀和加入
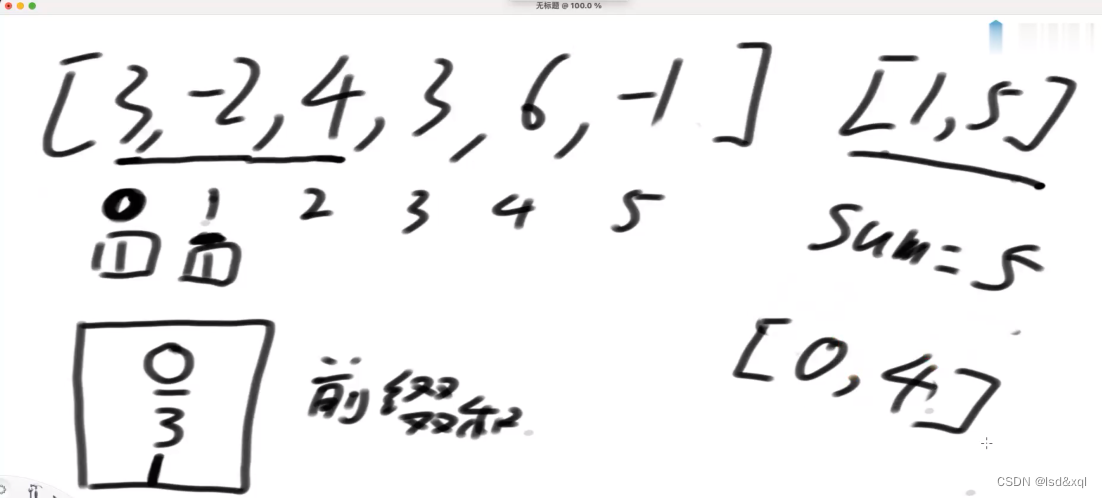
第三步:来到2位置,前缀和为5,那么需要找到有多少前缀和范围落在[0,4]范围上,发现有三个,再将5加入结构中。
依次类推下去得到最终的结果。
如何实现这个前缀和结构:
结构的特点:
1、这个结构能往里加整数
2、能够接收一个数字范围并且能够返回满足数字范围上的数有多少个
3、这个结构能接收重复的数字(我多个范围可能有相同的前缀和)
那么我可以做一个小于某个key值的接口把范围内的数给拼接出来。
问题:
有序表是不能有重复数字,解决方案:
我们可以将重复数字压在一起从而实现解决。
public class CountofRangeSum {
public static int countRangeSum1(int[] nums, int lower, int upper) {
int n = nums.length;
long[] sums = new long[n + 1];
for (int i = 0; i < n; ++i)
sums[i + 1] = sums[i] + nums[i];
return countWhileMergeSort(sums, 0, n + 1, lower, upper);
}
private static int countWhileMergeSort(long[] sums, int start, int end, int lower, int upper) {
if (end - start <= 1)
return 0;
int mid = (start + end) / 2;
int count = countWhileMergeSort(sums, start, mid, lower, upper)
+ countWhileMergeSort(sums, mid, end, lower, upper);
int j = mid, k = mid, t = mid;
long[] cache = new long[end - start];
for (int i = start, r = 0; i < mid; ++i, ++r) {
while (k < end && sums[k] - sums[i] < lower)
k++;
while (j < end && sums[j] - sums[i] <= upper)
j++;
while (t < end && sums[t] < sums[i])
cache[r++] = sums[t++];
cache[r] = sums[i];
count += j - k;
}
System.arraycopy(cache, 0, sums, start, t - start);
return count;
}
public static class SBTNode {
//参与排序的key
public long key;
//左孩子右孩子
public SBTNode l;
public SBTNode r;
//平衡因子
public long size; // 不同key的size
//附加的数据项
public long all; // 总的size
public SBTNode(long k) {
key = k;
size = 1;
all = 1;
}
}
public static class SizeBalancedTreeSet {
private SBTNode root;
private HashSet<Long> set = new HashSet<>();
private SBTNode rightRotate(SBTNode cur) {
long same = cur.all - (cur.l != null ? cur.l.all : 0) - (cur.r != null ? cur.r.all : 0);
SBTNode leftNode = cur.l;
cur.l = leftNode.r;
leftNode.r = cur;
leftNode.size = cur.size;
cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
// all modify
leftNode.all = cur.all;
cur.all = (cur.l != null ? cur.l.all : 0) + (cur.r != null ? cur.r.all : 0) + same;
return leftNode;
}
private SBTNode leftRotate(SBTNode cur) {
long same = cur.all - (cur.l != null ? cur.l.all : 0) - (cur.r != null ? cur.r.all : 0);
SBTNode rightNode = cur.r;
cur.r = rightNode.l;
rightNode.l = cur;
rightNode.size = cur.size;
cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
// all modify
rightNode.all = cur.all;
cur.all = (cur.l != null ? cur.l.all : 0) + (cur.r != null ? cur.r.all : 0) + same;
return rightNode;
}
private SBTNode maintain(SBTNode cur) {
if (cur == null) {
return null;
}
long leftSize = cur.l != null ? cur.l.size : 0;
long leftLeftSize = cur.l != null && cur.l.l != null ? cur.l.l.size : 0;
long leftRightSize = cur.l != null && cur.l.r != null ? cur.l.r.size : 0;
long rightSize = cur.r != null ? cur.r.size : 0;
long rightLeftSize = cur.r != null && cur.r.l != null ? cur.r.l.size : 0;
long rightRightSize = cur.r != null && cur.r.r != null ? cur.r.r.size : 0;
if (leftLeftSize > rightSize) {
cur = rightRotate(cur);
cur.r = maintain(cur.r);
cur = maintain(cur);
} else if (leftRightSize > rightSize) {
cur.l = leftRotate(cur.l);
cur = rightRotate(cur);
cur.l = maintain(cur.l);
cur.r = maintain(cur.r);
cur = maintain(cur);
} else if (rightRightSize > leftSize) {
cur = leftRotate(cur);
cur.l = maintain(cur.l);
cur = maintain(cur);
} else if (rightLeftSize > leftSize) {
cur.r = rightRotate(cur.r);
cur = leftRotate(cur);
cur.l = maintain(cur.l);
cur.r = maintain(cur.r);
cur = maintain(cur);
}
return cur;
}
private SBTNode add(SBTNode cur, long key, boolean contains) {
if (cur == null) {
return new SBTNode(key);
} else {
cur.all++;
if (key == cur.key) {
return cur;
} else { // 还在左滑或者右滑
if (!contains) {
cur.size++;
}
if (key < cur.key) {
cur.l = add(cur.l, key, contains);
} else {
cur.r = add(cur.r, key, contains);
}
return maintain(cur);
}
}
}
public void add(long sum) {
boolean contains = set.contains(sum);
root = add(root, sum, contains);
set.add(sum);
}
public long lessKeySize(long key) {
SBTNode cur = root;
long ans = 0;
while (cur != null) {
if (key == cur.key) {
//左树不为空则加上左树的all
return ans + (cur.l != null ? cur.l.all : 0);
} else if (key < cur.key) {
cur = cur.l;
} else {
ans += cur.all - (cur.r != null ? cur.r.all : 0);
cur = cur.r;
}
}
return ans;
}
// > 7 8...
// <8 ...<=7
public long moreKeySize(long key) {
return root != null ? (root.all - lessKeySize(key + 1)) : 0;
}
}
public static int countRangeSum2(int[] nums, int lower, int upper) {
// 黑盒,加入数字(前缀和),不去重,可以接受重复数字
//支持查询 < num , 有几个数?
SizeBalancedTreeSet treeSet = new SizeBalancedTreeSet();
long sum = 0;
int ans = 0;
treeSet.add(0);// 一个数都没有的时候,就已经有一个前缀和累加和为0,
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
//之前有多少个前缀和落在[sum - upper, sum - lower]
// [10, 20] ? 如果要查落在10到20范围上的数有多少个
// 那么需要查< 10 的有多少个 < 21 的有多少个
long a = treeSet.lessKeySize(sum - lower + 1);
long b = treeSet.lessKeySize(sum - upper);
//加上结果
ans += a - b;
//放入当前前缀和
treeSet.add(sum);
}
return ans;
}
// for test
public static void printArray(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
// for test
public static int[] generateArray(int len, int varible) {
int[] arr = new int[len];
for (int i = 0; i < arr.length; i++) {
arr[i] = (int) (Math.random() * varible);
}
return arr;
}
public static void main(String[] args) {
int len = 200;
int varible = 50;
for (int i = 0; i < 10000; i++) {
int[] test = generateArray(len, varible);
int lower = (int) (Math.random() * varible) - (int) (Math.random() * varible);
int upper = lower + (int) (Math.random() * varible);
int ans1 = countRangeSum1(test, lower, upper);
int ans2 = countRangeSum2(test, lower, upper);
if (ans1 != ans2) {
printArray(test);
System.out.println(lower);
System.out.println(upper);
System.out.println(ans1);
System.out.println(ans2);
}
}
}
}
有一个滑动窗口:
1)L是滑动窗口最左位置,R是滑动窗口最右位置,一开始LR都在数组左侧
2)任何一步都可能R往右移动表示某个数进了窗口
3)任何一步都可能L往右动,表示某个数出了窗口
想知道每一个窗口状态的中位数
还是想象有这样一个结构:
1)这个结构可以接收数字,也可以支持一个一个删除数也可以都删除
2)如果n等于奇数则取中间的数,如果为偶数则取中间两个数除以2
3)可以加入重复数字
public class SlidingWindowMedian {
public static class SBTNode<K extends Comparable<K>> {
public K key;
public SBTNode<K> l;
public SBTNode<K> r;
public int size;
public SBTNode(K k) {
key = k;
size = 1;
}
}
public static class SizeBalancedTreeMap<K extends Comparable<K>> {
private SBTNode<K> root;
private SBTNode<K> rightRotate(SBTNode<K> cur) {
SBTNode<K> leftNode = cur.l;
cur.l = leftNode.r;
leftNode.r = cur;
leftNode.size = cur.size;
cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
return leftNode;
}
private SBTNode<K> leftRotate(SBTNode<K> cur) {
SBTNode<K> rightNode = cur.r;
cur.r = rightNode.l;
rightNode.l = cur;
rightNode.size = cur.size;
cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
return rightNode;
}
private SBTNode<K> maintain(SBTNode<K> cur) {
if (cur == null) {
return null;
}
int leftSize = cur.l != null ? cur.l.size : 0;
int leftLeftSize = cur.l != null && cur.l.l != null ? cur.l.l.size : 0;
int leftRightSize = cur.l != null && cur.l.r != null ? cur.l.r.size : 0;
int rightSize = cur.r != null ? cur.r.size : 0;
int rightLeftSize = cur.r != null && cur.r.l != null ? cur.r.l.size : 0;
int rightRightSize = cur.r != null && cur.r.r != null ? cur.r.r.size : 0;
if (leftLeftSize > rightSize) {
cur = rightRotate(cur);
cur.r = maintain(cur.r);
cur = maintain(cur);
} else if (leftRightSize > rightSize) {
cur.l = leftRotate(cur.l);
cur = rightRotate(cur);
cur.l = maintain(cur.l);
cur.r = maintain(cur.r);
cur = maintain(cur);
} else if (rightRightSize > leftSize) {
cur = leftRotate(cur);
cur.l = maintain(cur.l);
cur = maintain(cur);
} else if (rightLeftSize > leftSize) {
cur.r = rightRotate(cur.r);
cur = leftRotate(cur);
cur.l = maintain(cur.l);
cur.r = maintain(cur.r);
cur = maintain(cur);
}
return cur;
}
private SBTNode<K> findLastIndex(K key) {
SBTNode<K> pre = root;
SBTNode<K> cur = root;
while (cur != null) {
pre = cur;
if (key.compareTo(cur.key) == 0) {
break;
} else if (key.compareTo(cur.key) < 0) {
cur = cur.l;
} else {
cur = cur.r;
}
}
return pre;
}
private SBTNode<K> add(SBTNode<K> cur, K key) {
if (cur == null) {
return new SBTNode<K>(key);
} else {
cur.size++;
if (key.compareTo(cur.key) < 0) {
cur.l = add(cur.l, key);
} else {
cur.r = add(cur.r, key);
}
return maintain(cur);
}
}
private SBTNode<K> delete(SBTNode<K> cur, K key) {
cur.size--;
if (key.compareTo(cur.key) > 0) {
cur.r = delete(cur.r, key);
} else if (key.compareTo(cur.key) < 0) {
cur.l = delete(cur.l, key);
} else {
if (cur.l == null && cur.r == null) {
// free cur memory -> C++
cur = null;
} else if (cur.l == null && cur.r != null) {
// free cur memory -> C++
cur = cur.r;
} else if (cur.l != null && cur.r == null) {
// free cur memory -> C++
cur = cur.l;
} else {
SBTNode<K> pre = null;
SBTNode<K> des = cur.r;
des.size--;
while (des.l != null) {
pre = des;
des = des.l;
des.size--;
}
if (pre != null) {
pre.l = des.r;
des.r = cur.r;
}
des.l = cur.l;
des.size = des.l.size + (des.r == null ? 0 : des.r.size) + 1;
// free cur memory -> C++
cur = des;
}
}
return cur;
}
private SBTNode<K> getIndex(SBTNode<K> cur, int kth) {
if (kth == (cur.l != null ? cur.l.size : 0) + 1) {
return cur;
} else if (kth <= (cur.l != null ? cur.l.size : 0)) {
return getIndex(cur.l, kth);
} else {
return getIndex(cur.r, kth - (cur.l != null ? cur.l.size : 0) - 1);
}
}
public int size() {
return root == null ? 0 : root.size;
}
public boolean containsKey(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
SBTNode<K> lastNode = findLastIndex(key);
return lastNode != null && key.compareTo(lastNode.key) == 0 ? true : false;
}
public void add(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
SBTNode<K> lastNode = findLastIndex(key);
if (lastNode == null || key.compareTo(lastNode.key) != 0) {
root = add(root, key);
}
}
public void remove(K key) {
if (key == null) {
throw new RuntimeException("invalid parameter.");
}
if (containsKey(key)) {
root = delete(root, key);
}
}
public K getIndexKey(int index) {
if (index < 0 || index >= this.size()) {
throw new RuntimeException("invalid parameter.");
}
return getIndex(root, index + 1).key;
}
}
public static class Node implements Comparable<Node> {
public int index;
public int value;
public Node(int i, int v) {
index = i;
value = v;
}
@Override
public int compareTo(Node o) {
return value != o.value ? Integer.valueOf(value).compareTo(o.value)
: Integer.valueOf(index).compareTo(o.index);
}
}
public static double[] medianSlidingWindow(int[] nums, int k) {
SizeBalancedTreeMap<Node> map = new SizeBalancedTreeMap<>();
for (int i = 0; i < k - 1; i++) {
map.add(new Node(i, nums[i]));
}
double[] ans = new double[nums.length - k + 1];
int index = 0;
for (int i = k - 1; i < nums.length; i++) {
map.add(new Node(i, nums[i]));
if (map.size() % 2 == 0) {
Node upmid = map.getIndexKey(map.size() / 2 - 1);
Node downmid = map.getIndexKey(map.size() / 2);
ans[index++] = ((double) upmid.value + (double) downmid.value) / 2;
} else {
Node mid = map.getIndexKey(map.size() / 2);
ans[index++] = (double) mid.value;
}
map.remove(new Node(i - k + 1, nums[i - k + 1]));
}
return ans;
}
}
高效实现ArrayList的add(index,num),get(index),remove(index)方法要求时间复杂度为LogN
假设维持一棵树A左边出现的点的自然时序都比它早,然后A的右树自然时序都比A晚,S的自然时序都比B早,k的自然时序都比B晚
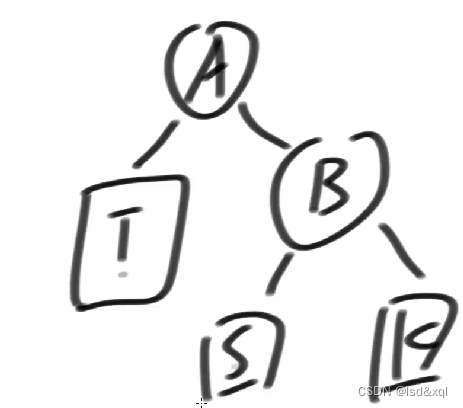
假设现在我们要左旋:
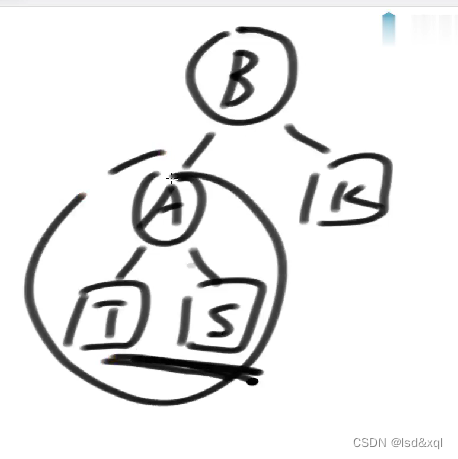
我的自然时序依然不变。
public class AddRemoveGetIndexGreat {
public static class SBTNode<V> {
public V value;
public SBTNode<V> l;
public SBTNode<V> r;
public int size;
public SBTNode(V v) {
value = v;
size = 1;
}
}
public static class SbtList<V> {
private SBTNode<V> root;
private SBTNode<V> rightRotate(SBTNode<V> cur) {
SBTNode<V> leftNode = cur.l;
cur.l = leftNode.r;
leftNode.r = cur;
leftNode.size = cur.size;
cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
return leftNode;
}
private SBTNode<V> leftRotate(SBTNode<V> cur) {
SBTNode<V> rightNode = cur.r;
cur.r = rightNode.l;
rightNode.l = cur;
rightNode.size = cur.size;
cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
return rightNode;
}
private SBTNode<V> maintain(SBTNode<V> cur) {
if (cur == null) {
return null;
}
int leftSize = cur.l != null ? cur.l.size : 0;
int leftLeftSize = cur.l != null && cur.l.l != null ? cur.l.l.size : 0;
int leftRightSize = cur.l != null && cur.l.r != null ? cur.l.r.size : 0;
int rightSize = cur.r != null ? cur.r.size : 0;
int rightLeftSize = cur.r != null && cur.r.l != null ? cur.r.l.size : 0;
int rightRightSize = cur.r != null && cur.r.r != null ? cur.r.r.size : 0;
if (leftLeftSize > rightSize) {
cur = rightRotate(cur);
cur.r = maintain(cur.r);
cur = maintain(cur);
} else if (leftRightSize > rightSize) {
cur.l = leftRotate(cur.l);
cur = rightRotate(cur);
cur.l = maintain(cur.l);
cur.r = maintain(cur.r);
cur = maintain(cur);
} else if (rightRightSize > leftSize) {
cur = leftRotate(cur);
cur.l = maintain(cur.l);
cur = maintain(cur);
} else if (rightLeftSize > leftSize) {
cur.r = rightRotate(cur.r);
cur = leftRotate(cur);
cur.l = maintain(cur.l);
cur.r = maintain(cur.r);
cur = maintain(cur);
}
return cur;
}
private SBTNode<V> add(SBTNode<V> root, int index, SBTNode<V> cur) {
if (root == null) {
return cur;
}
root.size++;
int leftAndHeadSize = (root.l != null ? root.l.size : 0) + 1;
if (index < leftAndHeadSize) {
root.l = add(root.l, index, cur);
} else {
root.r = add(root.r, index - leftAndHeadSize, cur);
}
root = maintain(root);
return root;
}
private SBTNode<V> remove(SBTNode<V> root, int index) {
root.size--;
int rootIndex = root.l != null ? root.l.size : 0;
if (index != rootIndex) {
if (index < rootIndex) {
root.l = remove(root.l, index);
} else {
root.r = remove(root.r, index - rootIndex - 1);
}
return root;
}
if (root.l == null && root.r == null) {
return null;
}
if (root.l == null) {
return root.r;
}
if (root.r == null) {
return root.l;
}
SBTNode<V> pre = null;
SBTNode<V> suc = root.r;
suc.size--;
while (suc.l != null) {
pre = suc;
suc = suc.l;
suc.size--;
}
if (pre != null) {
pre.l = suc.r;
suc.r = root.r;
}
suc.l = root.l;
suc.size = suc.l.size + (suc.r == null ? 0 : suc.r.size) + 1;
return suc;
}
private SBTNode<V> get(SBTNode<V> root, int index) {
int leftSize = root.l != null ? root.l.size : 0;
if (index < leftSize) {
return get(root.l, index);
} else if (index == leftSize) {
return root;
} else {
return get(root.r, index - leftSize - 1);
}
}
public void add(int index, V num) {
SBTNode<V> cur = new SBTNode<V>(num);
if (root == null) {
root = cur;
} else {
if (index <= root.size) {
root = add(root, index, cur);
}
}
}
public V get(int index) {
SBTNode<V> ans = get(root, index);
return ans.value;
}
public void remove(int index) {
if (index >= 0 && size() > index) {
root = remove(root, index);
}
}
public int size() {
return root == null ? 0 : root.size;
}
}
// 通过以下这个测试,
// 可以很明显的看到LinkedList的插入、删除、get效率不如SbtList
// LinkedList需要找到index所在的位置之后才能插入或者读取,时间复杂度O(N)
// SbtList是平衡搜索二叉树,所以插入或者读取时间复杂度都是O(logN)
public static void main(String[] args) {
// 功能测试
int test = 50000;
int max = 1000000;
boolean pass = true;
ArrayList<Integer> list = new ArrayList<>();
SbtList<Integer> sbtList = new SbtList<>();
for (int i = 0; i < test; i++) {
if (list.size() != sbtList.size()) {
pass = false;
break;
}
if (list.size() > 1 && Math.random() < 0.5) {
int removeIndex = (int) (Math.random() * list.size());
list.remove(removeIndex);
sbtList.remove(removeIndex);
} else {
int randomIndex = (int) (Math.random() * (list.size() + 1));
int randomValue = (int) (Math.random() * (max + 1));
list.add(randomIndex, randomValue);
sbtList.add(randomIndex, randomValue);
}
}
for (int i = 0; i < list.size(); i++) {
if (!list.get(i).equals(sbtList.get(i))) {
pass = false;
break;
}
}
System.out.println("功能测试是否通过 : " + pass);
// 性能测试
test = 500000;
list = new ArrayList<>();
sbtList = new SbtList<>();
long start = 0;
long end = 0;
start = System.currentTimeMillis();
for (int i = 0; i < test; i++) {
int randomIndex = (int) (Math.random() * (list.size() + 1));
int randomValue = (int) (Math.random() * (max + 1));
list.add(randomIndex, randomValue);
}
end = System.currentTimeMillis();
System.out.println("ArrayList插入总时长(毫秒) : " + (end - start));
start = System.currentTimeMillis();
for (int i = 0; i < test; i++) {
int randomIndex = (int) (Math.random() * (i + 1));
list.get(randomIndex);
}
end = System.currentTimeMillis();
System.out.println("ArrayList读取总时长(毫秒) : " + (end - start));
start = System.currentTimeMillis();
for (int i = 0; i < test; i++) {
int randomIndex = (int) (Math.random() * list.size());
list.remove(randomIndex);
}
end = System.currentTimeMillis();
System.out.println("ArrayList删除总时长(毫秒) : " + (end - start));
start = System.currentTimeMillis();
for (int i = 0; i < test; i++) {
int randomIndex = (int) (Math.random() * (sbtList.size() + 1));
int randomValue = (int) (Math.random() * (max + 1));
sbtList.add(randomIndex, randomValue);
}
end = System.currentTimeMillis();
System.out.println("SbtList插入总时长(毫秒) : " + (end - start));
start = System.currentTimeMillis();
for (int i = 0; i < test; i++) {
int randomIndex = (int) (Math.random() * (i + 1));
sbtList.get(randomIndex);
}
end = System.currentTimeMillis();
System.out.println("SbtList读取总时长(毫秒) : " + (end - start));
start = System.currentTimeMillis();
for (int i = 0; i < test; i++) {
int randomIndex = (int) (Math.random() * sbtList.size());
sbtList.remove(randomIndex);
}
end = System.currentTimeMillis();
System.out.println("SbtList删除总时长(毫秒) : " + (end - start));
}
}
红黑树的基本概念
1)AVL树它的平衡性来自于左树及右树的高度差小于等于1
2)SB树任何一个叔叔节点的个数不小于侄子节点,保证节点较少的树和节点较大的树的数量不超过两倍以上
红黑树定义
1)每个节点不是红就是黑
2)整棵树的头节点一定是黑,叶节点也一定为黑
3)节点有黑有红的情况下两个红节点不能相邻
4)每一颗子树任何一条链黑节点的数量要一样
最长的链条一定是红黑相间的,最短的链一定是只有黑节点的,且长度不会超过两倍以上。此优点是防止像AVL树一样删除和增加节点的时候就马上调整平衡性。对于硬盘的IO消耗比较低
插入有5种情况,删除有8种情况。


![Siemens-NXUG二次开发-新建与保存prt文件[Python UF][20231204]](https://img-blog.csdnimg.cn/direct/73898b7157724c6e876e0b1ed19e89b5.png#pic_center)