本文仅供学习,不作任何商业用途,严禁转载。绝大部分资料来自----数字集成电路——电路、系统与设计(第二版)及中国科学院段成华教授PPT
超大规模集成电路设计----MOS器件原理(二)
- 半导体物理知识补充
- 介绍
- 1. 半导体材料
- 2. 固体类型
- 二极管Diode
- The built-in potential barrier
- Concentrations
- 静态行为
- 1.理想二极管方程
- 2. 手工分析模型 Manual Analysis
- 3. 动态或者瞬态行为
- 对MOS器件的定性理解Qualitative understanding of MOS devices
- 晶体管及其参数的一般概述
- 电路符号symbols
- 分析MOS管的静态和动态效应
- The MOS Transistor under Static Conditions
- 1. The Threshold Voltage
- 2. Resistive Operation/线性工作
- 3. The Saturation Region
- 4. Channel-Length Modulation
- 5. Velocity Saturation
- 6. Drain Current versus Voltage Charts
- 7. Subthreshold Conduction
- 8. In Summary – Models for Manual Analysis
- 9. NMOS transistor modeled as a switch
- 二阶效应
- 用于手动分析的简单组件模型Simple component models for manual analysis
- SPICE的详细组件模型Detailed component models for SPICE
- 工艺变化的影响Impact of process variations
- FinFET:前景与挑战FinFET: The Promises and the Challenges
半导体物理知识补充
介绍
- 工程前提The engineering premise
It is a well-known premise in engineering that the conception of a complex construction without a prior understanding of the underlying building blocks is a sure road to failure.在工程学中,一个众所周知的前提是,在没有事先了解底层构建块的情况下,复杂结构的概念是一条必经之路。 - The goal
Our goal is to describe the functional operation of the devices, to highlight the properties and parameters that are particularly important in
the design of digital gates.我们的目标是描述设备的功能操作,突出在数字门设计中特别重要的特性和参数。 - The models
We present both first-order models for manual analysis as well as higher-order models for simulation for each component of interest.
我们提供了用于手动分析的一阶模型,以及用于模拟每个感兴趣组件的高阶模型。 - Actual parameters and process variations 实际参数和工艺变化
1. 半导体材料
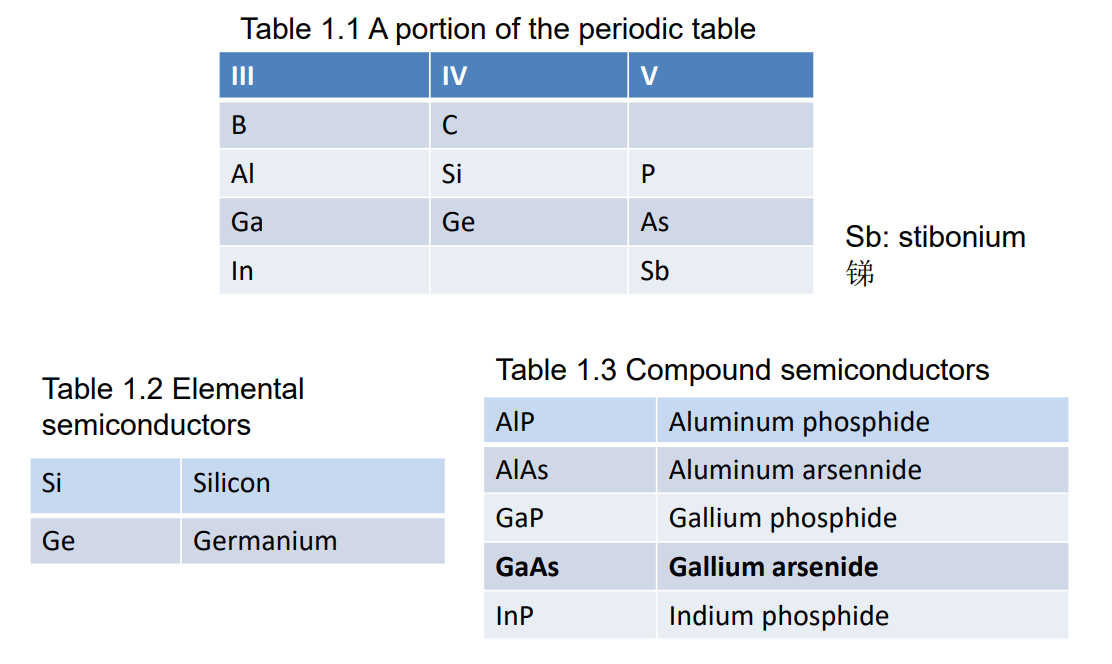
上面都是可以制作半导体的材料
2. 固体类型
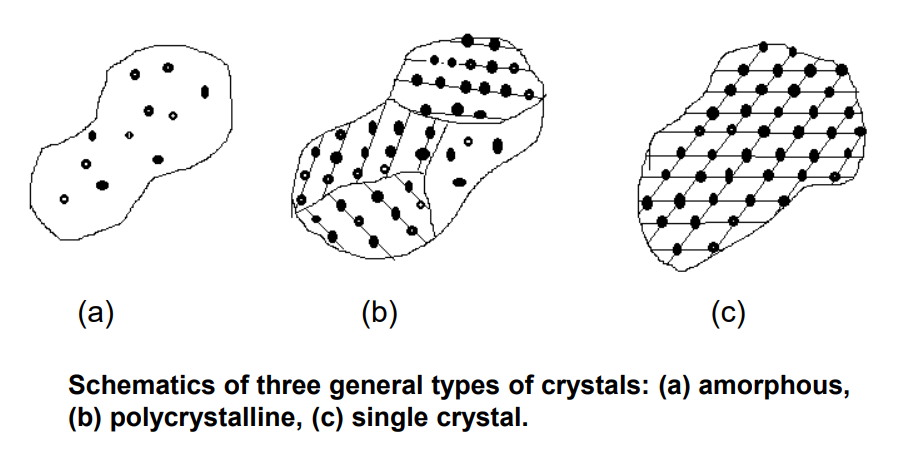
✓ 非晶体Amorphous materials have order only within a few atoms or molecular dimension.完全乱的
✓ 多晶Polycrystalline materials have a high degree of order over many atoms or molecular dimensions. 局部规则
✓ 单晶Single-crystal materials, ideally, have a high degree of order, or regular geometric periodicity, through the entire volume of the material. 全部规则
二极管Diode
- P型材料,一般是在硅里面掺杂硼B等三价材料,因为B三个电子,抢走了Si的一个电子,留下了空穴。所以叫P型材料,把B称为受主杂质(acceptor)
- N型材料,一般是在硅里面掺杂磷P等五价材料,因为P五个电子,多了一个电子,所以叫N型材料,把P称为施主杂质(donor)
我们把电子和空穴统称为载流子(carriers)。
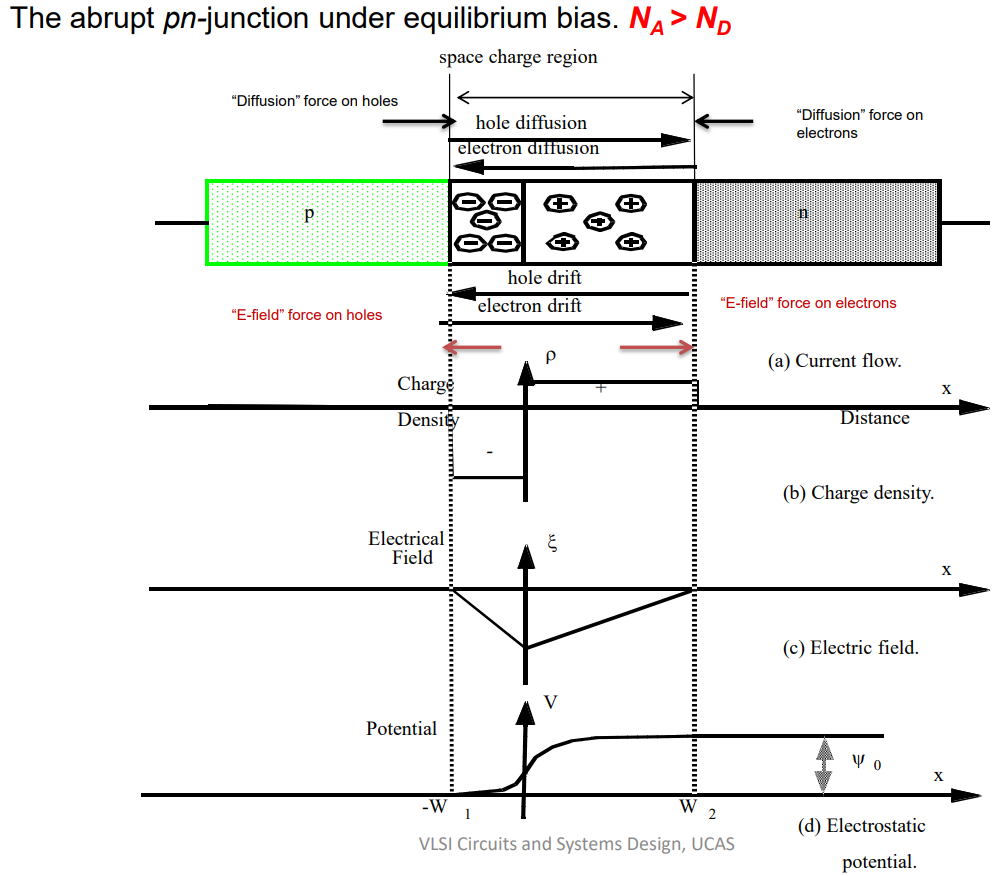
NA 和 ND 分别是 pn 结的 p 区和 n 区的受主杂质和施主杂质的浓度。
最初,边界处的电子和空穴浓度都存在较大的浓度梯度。多数载流子电子将开始从 n 区域扩散到 p 区域,多数载流子空穴将从 p 扩散到 n。在结点处,大多数载流子中和,留下固定(不动)受体和供体离子的区域(净带正电荷和负电荷)称为耗尽区或空间电荷区。 电荷在边界上产生一个电场,从 n 区引导到 p 区。 它使电子从 p 漂移到 n,空穴从 n 漂移到 p。
The built-in potential barrier
在零偏置下,结两端存在电压 Φ0,称为内建电势。
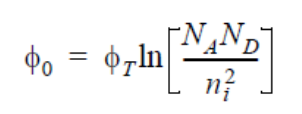
其中ΦT为热电压
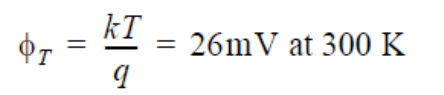
Concentrations
室温下,硅的本征载流子浓度
n
i
=
1.5
×
1
0
10
c
m
−
3
n_i= 1.5 \times10^{10} cm^{-3}
ni=1.5×1010cm−3
不同符号所表示浓度不同,如下图所示
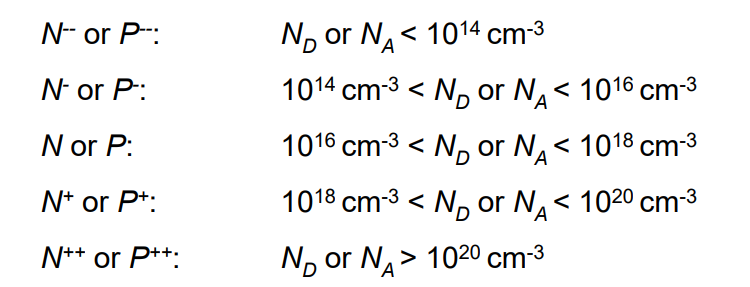
静态行为
1.理想二极管方程
I D = I S ( e V D / Φ T − 1 ) I_D=I_S\left(e^{V_D / \Phi_T}-1\right) ID=IS(eVD/ΦT−1)
ΦT是热电压,在室温下等于26 mV
IS 表示一个恒定值,称为二极管的饱和电流
2. 手工分析模型 Manual Analysis
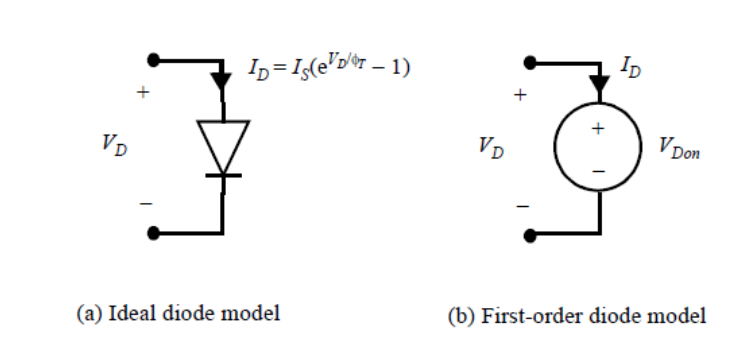
在一阶模型中,可以合理地假设导电二极管上有一个固定的压降
V
Don
V_{\text {Don }}
VDon 。虽然
V
Don
V_{\text {Don }}
VDon 的值取决于IS,但通常假定值为0.7 V。下面看一个例子。
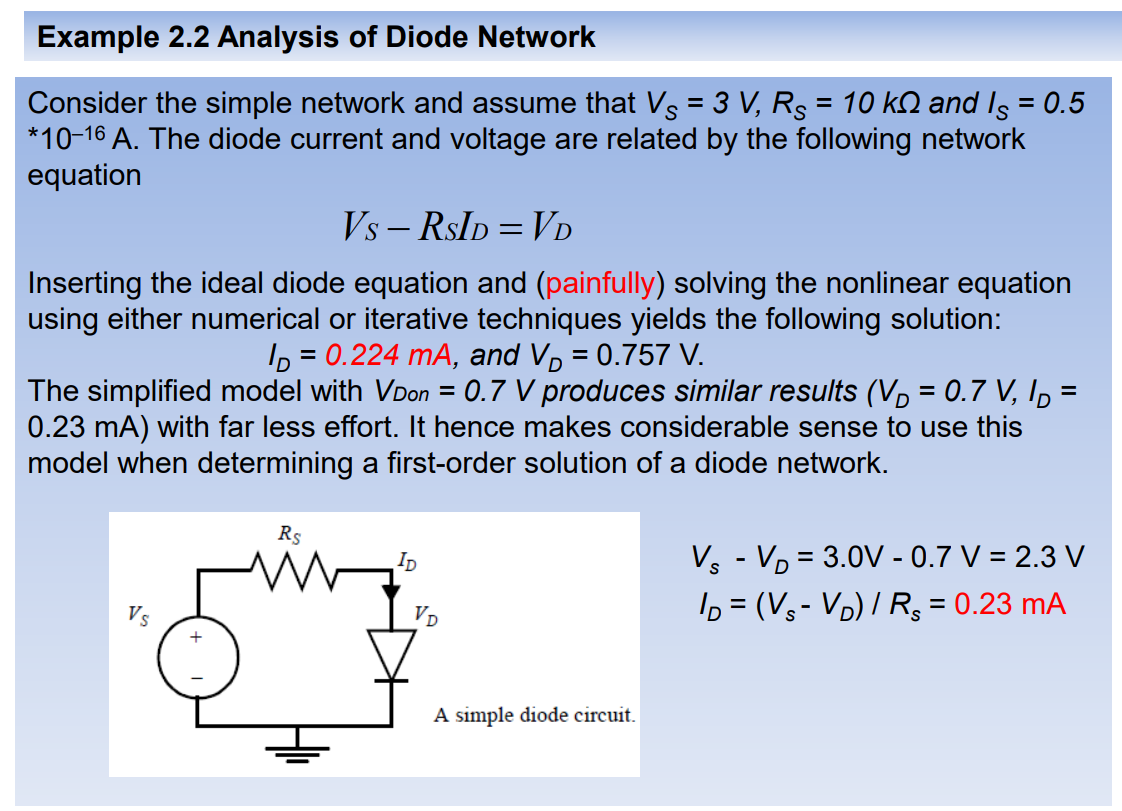
3. 动态或者瞬态行为
事实上,MOS数字集成电路中的所有二极管都是反向偏置的,并且在任何情况下都应该保持反向偏置。 因此,我们将只关注在反向偏置条件下控制二极管动态响应的因素,即耗尽区电荷。
- Depletion-Region Capacitance
(1) Depletion-region charge (VD is positive for forward bias).
Q j = A D ( 2 ε s i q N A N D N A + N D ) ( ϕ 0 − V D ) Q_j=A_D \sqrt{\left(2 \varepsilon_{s i} q \frac{N_A N_D}{N_A+N_D}\right)\left(\phi_0-V_D\right)} Qj=AD(2εsiqNA+NDNAND)(ϕ0−VD)
(2) Depletion-region width.
W j = W 2 − W 1 = ( 2 ε s i N A + N D q N A N D N A N D ) ( ϕ 0 − V D ) W_{j}=W_{2}-W_{1}=\sqrt{\left(\frac{2\varepsilon_{si}N_{A}+N_{D}}{q}\frac{N_{A}N_{D}}{N_{A}N_{D}}\right)(\phi_{0}-V_{D})} Wj=W2−W1=(q2εsiNA+NDNANDNAND)(ϕ0−VD)
(3) Maximum electric field.
E j = ( 2 q ε s i N A N D N A + N D ) ( ϕ 0 − V D ) E_j=\sqrt{\left(\frac{2q}{\varepsilon_{si}}\frac{N_AN_D}{N_A+N_D}\right)(\phi_0-V_D)} Ej=(εsi2qNA+NDNAND)(ϕ0−VD)
Φ0 is the built-in potential, ε s i ε_{si} εsi stands for the (相对介电常数)electrical permittivity of silicon and equals 11.7 times the permittivity of a vacuum. W2/(-W1) = NA/ND。 我们取硅的相对介电常数为11.7
A depletion-layer capacitance can be defined
C
j
=
d
Q
j
d
V
D
=
A
D
(
ε
i
q
2
N
A
N
D
N
A
+
N
D
)
(
ϕ
0
−
V
D
)
−
1
=
C
j
0
1
−
V
D
/
ϕ
0
\begin{aligned}C_j&=\frac{\mathrm{d}Q_j}{\mathrm{d}V_D}=A_D\sqrt{\left(\frac{\varepsilon_iq}{2}\frac{N_AN_D}{N_A+N_D}\right)(\phi_0-V_D)^{-1}}\\&=\frac{C_{j0}}{\sqrt{1-V_D/\phi_0}}\end{aligned}
Cj=dVDdQj=AD(2εiqNA+NDNAND)(ϕ0−VD)−1=1−VD/ϕ0Cj0
where
C
j
0
C_{j0}
Cj0 is the capacitance under zero-bias conditions and is only a function of the physical parameters of the device.
C
j
0
=
A
D
(
ε
s
i
q
2
N
A
N
D
N
A
+
N
D
)
ϕ
0
−
1
C_{j0}=A_{D}\sqrt{\left(\frac{\varepsilon_{si}q}{2}\frac{N_{A}N_{D}}{N_{A}+N_{D}}\right)\phi_{0}^{-1}}
Cj0=AD(2εsiqNA+NDNAND)ϕ0−1
对于线性梯度结,可以提供结电容的更通用表达式
C
j
=
C
j
0
(
1
−
V
D
/
ϕ
0
)
m
C_j=\frac{C_{j0}}{(1-V_D/\phi_0)^m}
Cj=(1−VD/ϕ0)mCj0 重要公式,需要记住!
where
m
m
m is called the grading coefficient and equals 1/2 for the abrupt junction and 1/3 for the linear or graded junction.
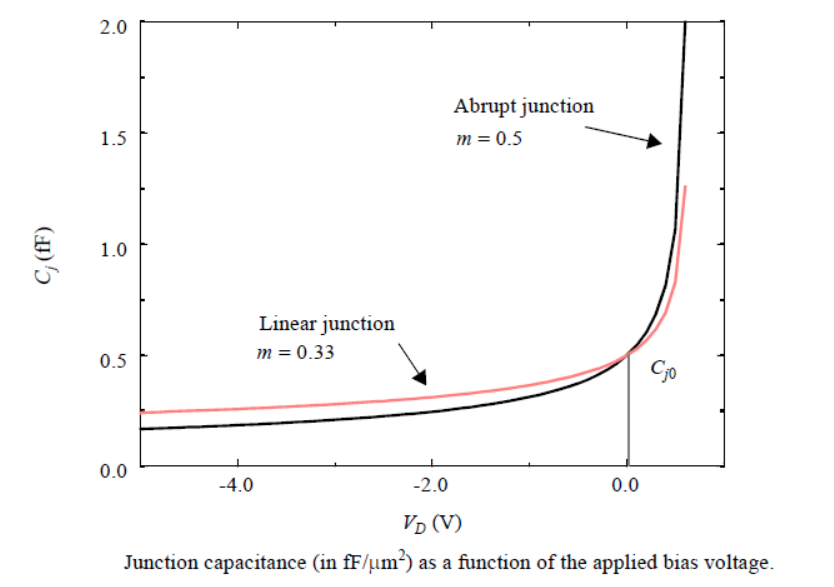
可以观察到很强的非线性依赖性。另请注意,电容会随着反向偏置的增加而减小:5 V的反向偏置会使电容减小两倍以上
- 大信号耗尽区电容
定义了一个等效的线性电容 C e q C_{eq} Ceq,即对于从电压 V h i g h V_{high} Vhigh 到 V l o w V_{low} Vlow, 的给定电压摆幅,转移的电荷量与非线性模型预测的电荷量相同。意思就是说,就是我们定义一个等效电容,让这个等效电容反偏电压变化与真实二极管电压变化一致,用真实二极管电容变化的电荷量,比上这个电压变化量,就是等效电容 C e q C_{eq} Ceq的大小。
C e q = Δ Q j Δ V D = Q j ( V h i g h ) − Q j ( V l o w ) V h i g h − V l o w = K e q C j 0 C_{eq}=\frac{\Delta Q_{j}}{\Delta V_{D}}=\frac{Q_{j}(V_{high})-Q_{j}(V_{low})}{V_{high}-V_{low}}=K_{eq}C_{j0} Ceq=ΔVDΔQj=Vhigh−VlowQj(Vhigh)−Qj(Vlow)=KeqCj0
K e q = − ϕ 0 m ( V h i g h − V l o w ) ( 1 − m ) [ ( ϕ 0 − V h i g h ) 1 − m − ( ϕ 0 − V l o w ) 1 − m ] K_{eq}=\frac{-\phi_{0}^{m}}{(V_{high}-V_{low})(1-m)}[(\phi_{0}-V_{high})^{1-m}-(\phi_{0}-V_{low})^{1-m}] Keq=(Vhigh−Vlow)(1−m)−ϕ0m[(ϕ0−Vhigh)1−m−(ϕ0−Vlow)1−m]
对MOS器件的定性理解Qualitative understanding of MOS devices
The workhorse of contemporary digital design!
✓ Performing very well as a switch;开关特性
✓ Introducing little parasitic effects;
✓ Heave integration density ;
✓ Relatively “simple” manufacturing process; 制作工艺相对简单
✓ Producing large and complex circuits in an economical way.
晶体管及其参数的一般概述
A general overview of the transistor and its parameters
CMOS (Complementary MOS): NMOS + PMOS
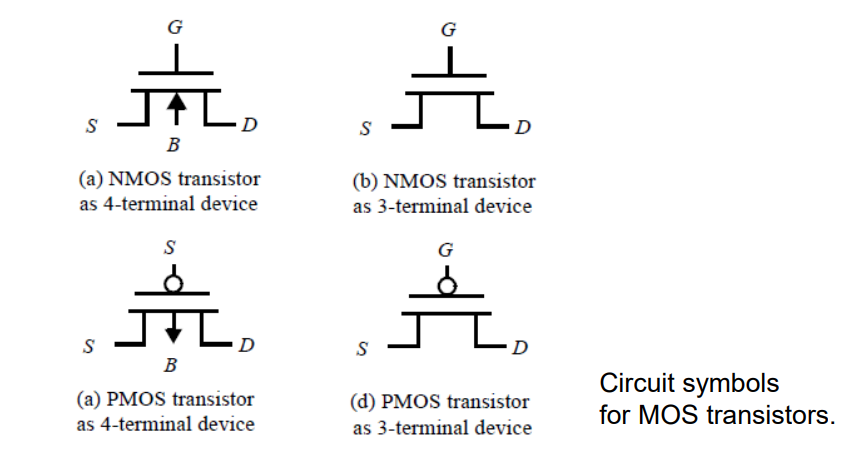
NMOS transistor: n+ drain and source regions, embedded in a p-type substrate. The current is carried by electrons moving through an n-type channel between source and drain
PMOS device: p+ drain and source regions, using an n-type substrate . The current is carried by holes moving through a p-type channel.
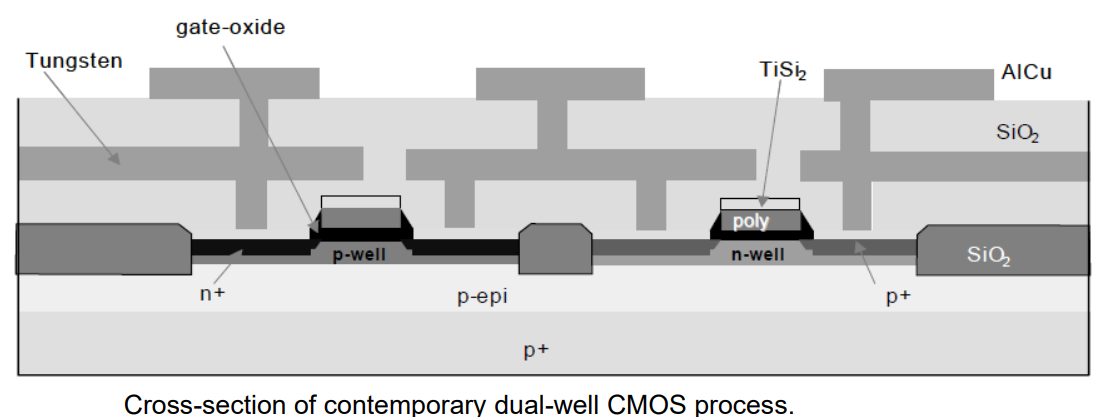
电路符号symbols
If the fourth terminal is not shown, it is assumed that the body is connected to the appropriate supply.
分析MOS管的静态和动态效应
An analytical description of the transistor from a static (steady state) and dynamic (transient) viewpoint
The MOS Transistor under Static Conditions
1. The Threshold Voltage
- The depletion region
正的栅极电压导致正电荷在栅极上积聚,负电荷积聚在衬底侧。后者最初通过排斥移动的空穴来表现出来。因此,在栅极下方形成一个耗尽区。
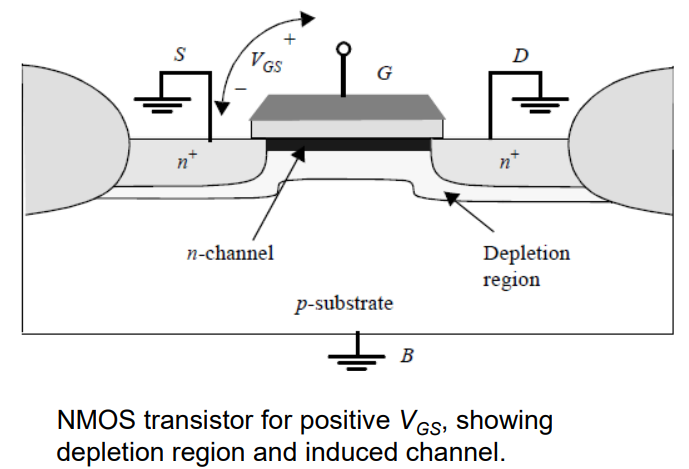
The width:
W
d
=
2
ε
s
i
ϕ
q
N
A
W_d=\sqrt{\frac{2\varepsilon_{si}\phi}{qN_A}}
Wd=qNA2εsiϕ
The space charge per unit area:
Q
d
=
−
2
q
N
A
ε
s
i
ϕ
Q_d=-\sqrt{2qN_A\varepsilon_{si}\phi}
Qd=−2qNAεsiϕ
NA为衬底掺杂,Φ为耗尽层两端的电压(即氧化物-硅边界处的电位)
- Strong inversion layer
随着栅极电压 (VGS) 的增加,硅表面的电位 (ΦS) 在某个点达到临界值,此时半导体表面反转为 n 型材料。该点标志着一种称为强反转的现象的开始,并且发生在等于费米势两倍的电压(ΦF = -0.3 V,对于典型的p型硅衬底)下:
ϕ
F
=
−
ϕ
T
l
n
(
N
A
n
i
)
Φ
S
:
Φ
F
→
−
Φ
F
Φ
=
Φ
S
−
Φ
F
=
2
∣
Φ
F
∣
\begin{aligned} &\phi_{F}=-\phi_{T}\mathrm{ln}(\frac{N_{A}}{n_{i}}) \\ &\mathbf{\Phi}_{S}:\mathbf{\Phi}_{F}\rightarrow-\mathbf{\Phi}_{F} \\ &\Phi=\Phi_{S}-\Phi_{F}=2\left|\Phi_{F}\right| \end{aligned}
ϕF=−ϕTln(niNA)ΦS:ΦF→−ΦFΦ=ΦS−ΦF=2∣ΦF∣
费米能级定义为在平衡系统中电子占据空态的概率为 50% 的线。
For n-type silicon substrate
Φ
F
n
=
k
T
q
ln
N
D
n
i
>
0
\Phi_{Fn}=\frac{kT}q\ln\frac{N_D}{n_i}>0
ΦFn=qkTlnniND>0
Strong inversion
Φ
≥
2
∣
Φ
F
∣
\Phi \ge 2|\Phi_F|
Φ≥2∣ΦF∣
Weak inversion
∣
Φ
F
∣
≤
Φ
≤
2
∣
Φ
F
∣
|\Phi_F|\leq\Phi\leq2\left|\Phi_F\right|
∣ΦF∣≤Φ≤2∣ΦF∣
Depletion
0
≤
Φ
≤
∣
Φ
F
∣
0\leq\Phi\leq\mid\Phi_F\mid
0≤Φ≤∣ΦF∣
在
Φ
=
2
∣
Φ
F
∣
\Phi=2\left|\Phi_F\right|
Φ=2∣ΦF∣的条件下,表面移动电子的密度等于原始衬底或体中移动空穴的密度。
- Depletion region charge with an inverse layer
In the presence of an inversion layer, the charge stored in the depletion region is fixed and equals (p-type substrate) - The threshold voltage VT
The value of VGS where strong inversion occurs is called the threshold voltage VT.
VT is a function of several components, most of which are material constants:
(1) the difference in work-function between gate and substrate material,
(2) the oxide thickness,
(3) the Fermi voltage,
(4) the charge of impurities trapped at the surface between channel and gate oxide,
(5) the dosage of ions implanted for threshold adjustment, and
(6) the source-bulk voltage VSB has an impact on the threshold as well
We rely on an empirical parameter called VT0, which is the threshold voltage for VSB = 0.
V
T
=
V
T
0
+
γ
(
∣
−
2
ϕ
F
+
V
S
B
∣
−
∣
−
2
ϕ
F
∣
)
V_{T}=V_{T0}+\gamma(\sqrt{\left|-2\phi_{F}+V_{SB}\right|}-\sqrt{\left|-2\phi_{F}\right|})
VT=VT0+γ(∣−2ϕF+VSB∣−∣−2ϕF∣)
The parameter γ (gamma) is called the body-effect coefficient, and expresses the impact of changes in VSB.
γ
=
1
C
o
x
2
q
ε
s
i
N
A
\gamma=\frac1{Cox}\sqrt{2q\varepsilon_{si}N_A}
γ=Cox12qεsiNA 体效应系数的公式要记住
Observe that the threshold voltage has a positive value for a typical NMOS device, while it is negative for a normal PMOS transistor
For NMOS, VT > 0
For PMOS, VT < 0
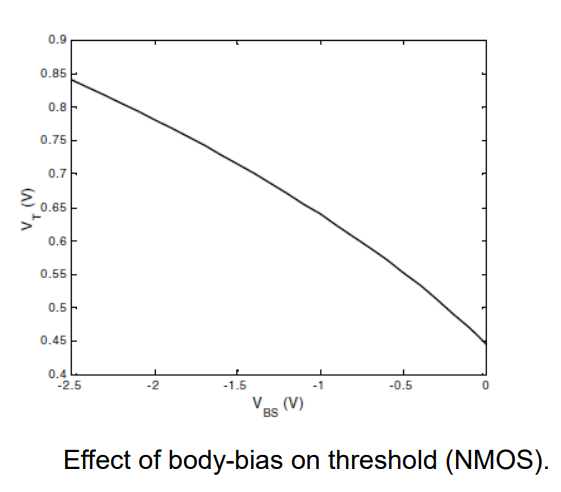
下面来看一道例题

注意,二氧化硅的相对介电常数为3.97,硅的相对介电常数为11.7
2. Resistive Operation/线性工作
I
D
=
κ
n
′
W
L
[
(
V
G
S
−
V
T
)
V
D
S
−
V
D
S
2
2
]
I
D
=
κ
n
[
(
V
G
S
−
V
T
)
V
D
S
−
V
D
S
2
2
]
\begin{gathered} I_D \begin{aligned}=\kappa_{n}'\frac{W}{L}\Bigg[(V_{GS}-V_{T})V_{DS}-\frac{V_{DS}^{2}}{2}\Bigg]\end{aligned} \\ I_D =\kappa_n\Biggl[(V_{GS}-V_T)V_{DS}-\frac{V_{DS}^2}2\Biggr] \end{gathered}
ID=κn′LW[(VGS−VT)VDS−2VDS2]ID=κn[(VGS−VT)VDS−2VDS2]
K
n
′
=
μ
n
C
o
x
=
μ
n
E
o
x
t
o
x
{K_n}^{\prime}=\mu_nC_{ox}=\frac{\mu_n{\mathcal E}_{ox}}{t_{ox}}
Kn′=μnCox=toxμnEox
κ
n
=
κ
n
’
W
L
\kappa_n=\kappa_n’\frac WL
κn=κn’LW这是增益因子
有效沟道长度和宽度的概念:
由于源极和漏极区域 (L) 的横向扩散和隔离场氧化物 (W) 的侵占,
W
=
W
D
−
Δ
W
L
=
L
D
−
Δ
L
\begin{aligned}W&=W_D-\Delta W\\L&=L_D-\Delta L\end{aligned}
WL=WD−ΔW=LD−ΔL
其中 D 下标标记的数量是在画版图时的绘制尺寸。
3. The Saturation Region
感应电荷为零,导电通道消失或被捏断时处于饱和区
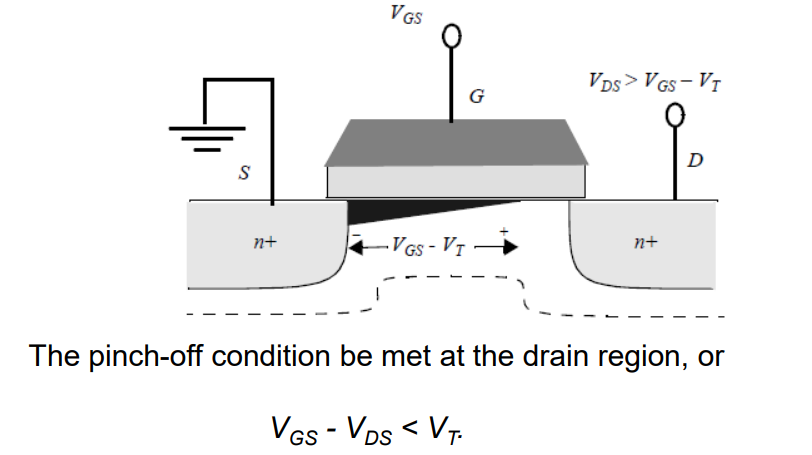
饱和区大信号电流方程
I
D
S
A
T
=
1
2
κ
n
’
W
L
(
V
G
S
−
V
T
)
2
I_{DSAT}=\frac12\kappa_n’\frac WL(V_{GS}-V_T)^2
IDSAT=21κn’LW(VGS−VT)2
4. Channel-Length Modulation
VDS的增加会导致漏极结处的耗尽区增大,从而缩短有效通道的长度。
I
D
=
I
D
′
(
1
+
λ
V
D
S
)
I_{D}=I_{D}{'}(1+\lambda V_{DS})
ID=ID′(1+λVDS)
其中 ID ’ 是先前推导的电流表达式,λ 是经验参数,称为沟道长度调制。
λ
∝
1
L
\lambda\propto\frac1L
λ∝L1
5. Velocity Saturation
==首先速度饱和效应不是短沟道效应!但是也是短沟道器件具有的特点!==具有极短沟道长度的晶体管(称为短沟道器件)的行为与前几段中介绍的电阻和饱和模型有很大不同。造成这种缺陷的罪魁祸首是速度饱和效应。
当沿沟道的电场达到临界值ξc时,由于散射效应(载流子遭受碰撞),载流子的速度趋于饱和。
我们直接记忆由于速度饱和而修正后的线性区和饱和区公式。
线性区:
I
D
=
μ
n
C
o
x
(
W
L
)
[
(
V
G
S
−
V
T
)
V
D
S
−
V
D
S
2
2
]
κ
(
V
D
S
)
I_D=\mu_nC_{ox}(\frac WL)[(V_{GS}-V_T)V_{DS}-\frac{V_{DS}^2}2]\kappa(V_{DS})
ID=μnCox(LW)[(VGS−VT)VDS−2VDS2]κ(VDS)
其中
κ
(
V
)
=
1
1
+
(
V
/
(
ξ
c
L
)
)
=
1
1
+
(
V
/
L
)
/
ξ
c
\kappa(V)=\frac1{1+\left(V/\left(\xi_cL\right)\right)}=\frac1{1+\left(V/L\right)/\xi_c}
κ(V)=1+(V/(ξcL))1=1+(V/L)/ξc1
另外注意,这里的
κ
\kappa
κ函数代入的是VDS
饱和区:
V
D
S
A
T
=
V
G
T
ξ
c
L
V
G
T
+
ξ
c
L
=
κ
(
V
G
T
)
V
G
T
I
D
S
A
T
=
ν
s
a
t
C
o
x
(
V
G
S
−
V
T
−
V
D
S
A
T
)
W
=
ν
s
a
t
C
o
x
W
V
G
T
2
V
G
T
+
ξ
c
L
\begin{aligned}V_{DSAT}&=\frac{V_{GT}\xi_cL}{V_{GT}+\xi_cL}=\kappa(V_{GT})V_{GT}\\I_{DSAT}&=\nu_{sat}C_{ox}(V_{GS}-V_T-V_{DSAT})W=\nu_{sat}C_{ox}W\frac{V_{GT}^2}{V_{GT}+\xi_cL}\end{aligned}
VDSATIDSAT=VGT+ξcLVGTξcL=κ(VGT)VGT=νsatCox(VGS−VT−VDSAT)W=νsatCoxWVGT+ξcLVGT2
其中
κ
(
V
)
=
1
1
+
(
V
/
(
ξ
c
L
)
)
=
1
1
+
(
V
/
L
)
/
ξ
c
\kappa(V)=\frac1{1+\left(V/\left(\xi_cL\right)\right)}=\frac1{1+\left(V/L\right)/\xi_c}
κ(V)=1+(V/(ξcL))1=1+(V/L)/ξc1
另外注意,这里的
κ
\kappa
κ函数代入的是VGT ,VGT= VGS-VTH
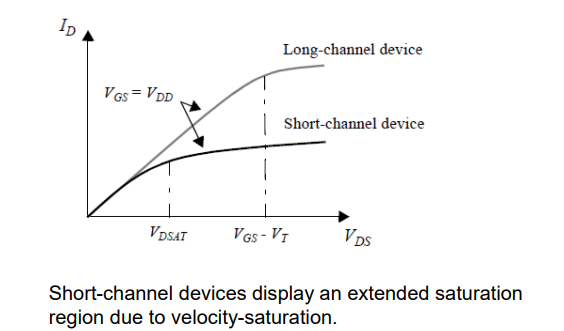
对于短通道器件和足够大的 VGT 值,k(VGT) 明显小于 1,因此 VDSAT < VGT。器件在 VDS 达到 VGS - VT 之前进入饱和状态。
要记住沟道长度调制效应同样会影响速度饱和!
I
D
S
A
T
=
I
D
S
A
T
(
1
+
λ
V
D
S
)
I_{DSAT}=I_{DSAT}\left(1+\lambda V_{DS}\right)
IDSAT=IDSAT(1+λVDS)
同时载流子迁移率un也是会改变的。
μ
n
,
e
f
f
=
μ
n
0
1
+
η
(
V
G
S
−
V
T
)
\mu_{n,eff}=\frac{\mu_{n0}}{1+\eta(V_{GS}-V_T)}
μn,eff=1+η(VGS−VT)μn0
下面我们来看两道例题


上面两个例题都是在这个假定之下的
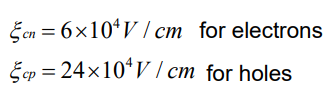
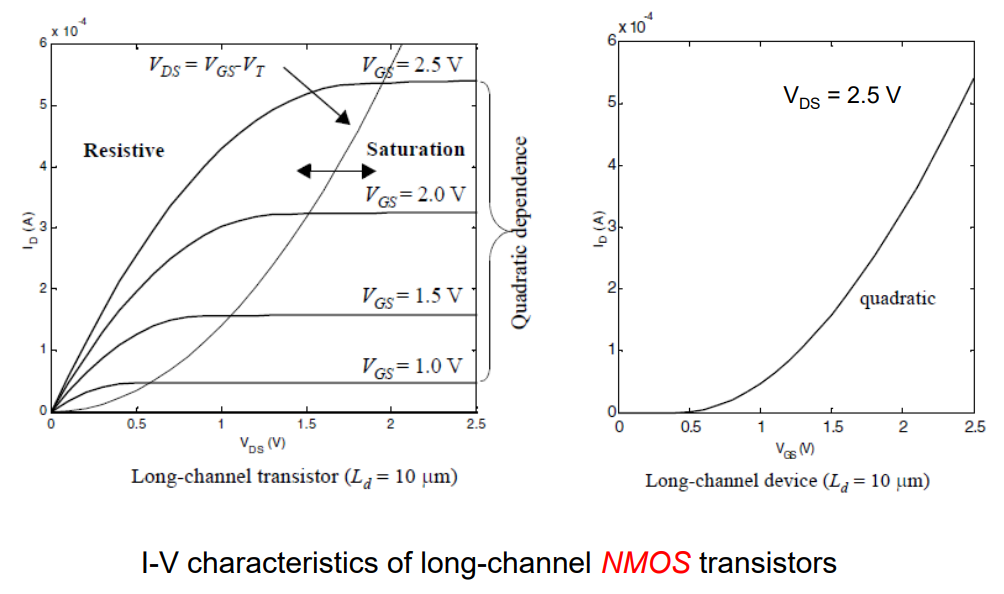
6. Drain Current versus Voltage Charts
采用0.25 μm CMOS技术的长沟道和短沟道NMOS晶体管的I-V特性。两个晶体管的 (W/L) 比率相同,等于 1.5
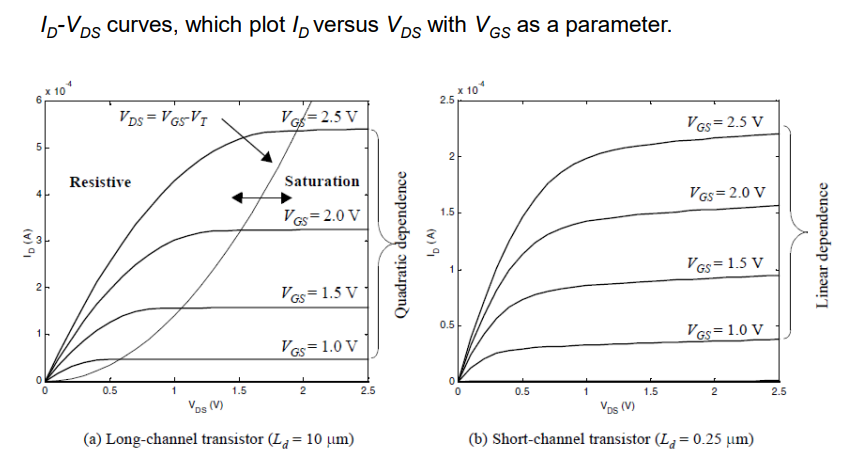
NMOS晶体管ID-VGS特性,适用于长沟道和短沟道器件(0.25μm CMOS技术)。W/L = 1.5(两个晶体管),VDS = 2.5 V
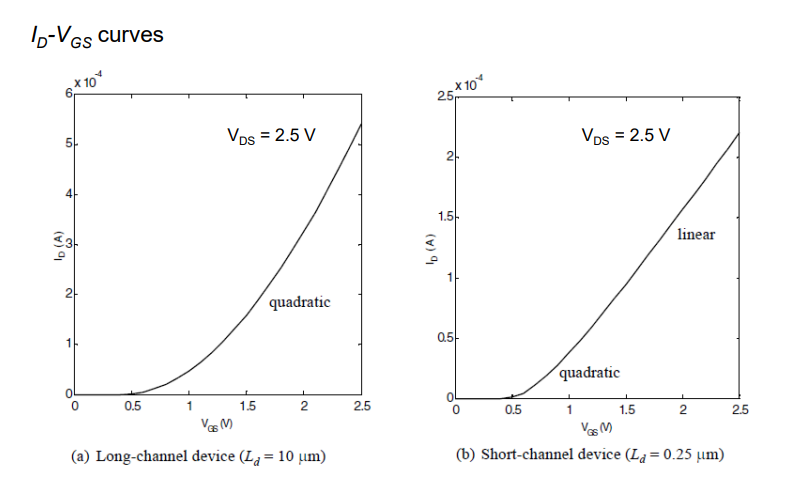
7. Subthreshold Conduction
8. In Summary – Models for Manual Analysis
9. NMOS transistor modeled as a switch
二阶效应
Some second-order effects