系列文章目录
MATLAB 模型参考自适应控制 - Model Reference Adaptive Control
文章目录
- 系列文章目录
- 前言
- 一、控制器结构
- 1.1 一阶逼近
- 1.2 二阶逼近
- 二、指定控制器参数
- 参考
前言
自抗扰控制 (ADRC) 是一种无模型控制方法,适用于为具有未知动态特性以及内部和外部扰动的被控对象设计控制器。此算法只需要对被控对象动态特性进行逼近,即可设计具有稳健抗扰功能的无超调的控制器。
您可以使用 Active Disturbance Rejection Control 模块来实现 ADRC。该模块使用已知系统动态特性的一阶或二阶模型逼近以及建模为被控对象的扩张状态的未知动态特性和扰动。通常,您可以根据工作范围内被控对象的开环阶跃响应来确定此阶数。
一阶逼近 - y ˙ ( t ) = b 0 u ( t ) + f ( t ) {\dot{y}}(t)=b 0 u(t)+f(t) y˙(t)=b0u(t)+f(t)
二阶逼近 - y ¨ ( t ) = b 0 u ( t ) + f ( t ) {\ddot{y}}(t)=b 0 u(t)+f(t) y¨(t)=b0u(t)+f(t)
其中:
-
y(t) 是被控对象输出。
-
u(t) 是输入信号。
-
b0 是临界增益,它是描述被控对象对输入 u(t) 的响应的估计增益。
-
f(t) 是总扰动,包括未知动态特性扰动和其他扰动。
该模块使用扩张状态观测器 (ESO) 来估计 f(t),并通过减少估计的扰动对模型逼近已知部分的影响来实现抗扰控制。
您可以实现离散时间和连续时间控制器。设置控制器时域和采样时间以匹配被控对象模型的时域。
一、控制器结构
1.1 一阶逼近
对于一阶被控对象模型逼近
y
˙
(
t
)
=
b
0
u
(
t
)
+
f
(
t
)
{\dot{y}}(t)=b0u(t)+f(t)
y˙(t)=b0u(t)+f(t),被控对象输出状态是
x
1
=
y
(
t
)
x_{1}=\mathrm{y}(t)
x1=y(t) ,扩张状态是
x
2
=
f
(
t
)
x_{2}=\mathrm{f}(t)
x2=f(t)
状态空间模型如下。
x
˙
=
A
x
+
B
u
+
(
0
f
˙
(
t
)
)
{{\dot{x}=A x+B u+\left(\begin{array}{c}{{0}}\\ {{\dot{f}(t)}}\end{array}\right)}}
x˙=Ax+Bu+(0f˙(t))
y
=
C
x
,
y=C x,
y=Cx,
其中
A = ( 0 1 0 0 ) , B = ( b 0 0 ) , C = ( 1 0 ) . A=\begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix},\ B=\begin{pmatrix} b0 \\ 0 \end{pmatrix},C=(1\ 0). A=(0010), B=(b00),C=(1 0).
对于此可观测系统,模块使用龙伯格观测器来提供被控对象状态和总扰动的估计值。使用估计的状态
z 1 = y ^ ( t ) z 2 = f ^ ( t ) , \begin{array}{c}{{z_{1}=\hat{y}(t)}}\\ {{z_{2}=\hat{f}(t),}}\end{array} z1=y^(t)z2=f^(t),
控制器计算控制输入 u(t),如下所示。
u ( t ) = u 0 ( t ) − z 2 b 0 , u(t)={\dfrac{u0(t)-z2}{b0}}, u(t)=b0u0(t)−z2,
其中
u 0 ( t ) = K P ( r ( t ) − z 1 ) . u\mathrm{0}(t)=K P(r(t)-z1). u0(t)=KP(r(t)−z1).
这是一个基于估计的状态反馈控制器,当估计值和实际值相等时,系统具有一阶闭环行为。此闭环系统具有极点 s = –KP。
此控制器表示为以下控制结构。
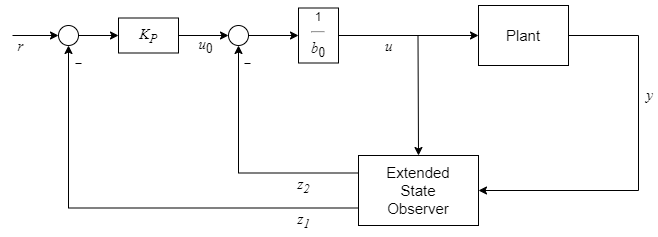
为了简化控制器调节,该模块将控制器极点设置在 (s + ωc) 处,将观测器极点设置在 ( s + ω 0 ) 2 (s+\omega_{0})^{2} (s+ω0)2 处,其中 ωc 和 ωo 分别为控制器带宽和观测器带宽。
1.2 二阶逼近
对于二阶被控对象模型逼近 y ¨ ( t ) = b 0 u ( t ) + f ( t ) \ddot{y}(t)=b{0}u(t)+f(t) y¨(t)=b0u(t)+f(t) ,被控对象输出状态是 x 1 = y ( t ) x_{1}=\mathrm{y}(t) x1=y(t) 和 x 2 = y ˙ ( t ) x_{2}=\mathrm{\dot{y}}(t) x2=y˙(t) ,扩张状态是 x 3 = f ( t ) x_{3}=\mathrm{f}(t) x3=f(t)
状态空间模型如下。
x ˙ = A x + B u + ( 0 0 f ˙ ( t ) ) \dot{x}=A x+B u+\left(\begin{array}{c}{{0}}\\ {{0}}\\ {{\dot{f}(t)}}\end{array}\right) x˙=Ax+Bu+ 00f˙(t)
y = C x , y=C x, y=Cx,
其中
A = ( 0 1 0 0 0 1 0 0 0 ) , B = ( 0 b 0 0 ) , C = ( 1 0 0 ) . A={\left(\begin{array}{l l l}{0}&{1}&{0}\\ {0}&{0}&{1}\\ {0}&{0}&{0}\end{array}\right)},B={\left(\begin{array}{l l}{0}\\ {b0}\\ {0}\end{array}\right)},C=(1\quad0\quad0). A= 000100010 ,B= 0b00 ,C=(100).
对于此可观测系统,模块使用龙伯格观测器来提供被控对象状态和总扰动的估计值。使用估计的状态
z 1 = y ^ ( t ) z 2 = y ˙ ^ ( t ) z 3 = f ^ ( t ) , \begin{array}{c}{{z_{1}=\hat{y}(t)}}\\{{z_{2}=\hat{\dot{y}}(t)}} \\ {{z_{3}=\hat{f}(t),}}\end{array} z1=y^(t)z2=y˙^(t)z3=f^(t),
控制器计算控制输入 u(t),如下所示。
u ( t ) = u 0 ( t ) − z 3 b 0 , u(t)={\dfrac{u0(t)-z3}{b0}}, u(t)=b0u0(t)−z3,
其中
u 0 ( t ) = K P ( r ( t ) − z 1 ) − K D z 2. u\mathrm{0}(t)=K P(r(t)-z1)-K D z2. u0(t)=KP(r(t)−z1)−KDz2.
这是一个基于估计的状态反馈控制器,当估计值和实际值相等时,系统具有二阶闭环行为。
此控制器表示为以下控制结构。
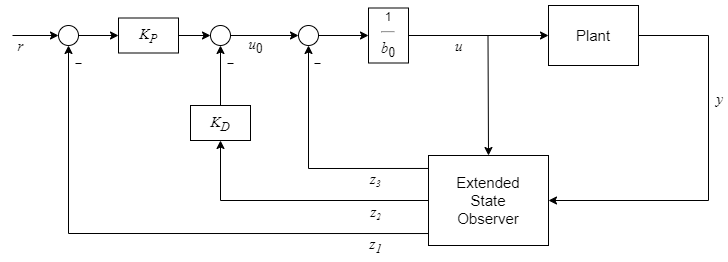
为了简化控制器调节,该模块分别将控制器极点设置在
(
s
+
ω
0
)
2
(s+\omega_{0})^{2}
(s+ω0)2 处,将观测器极点设置在
(
s
+
ω
0
)
3
(s+\omega_{0})^{3}
(s+ω0)3 处,其中 ωc 和 ωo 分别为控制器带宽和观测器带宽。
二、指定控制器参数
为了对您的被控对象实现 ADRC,您必须为被控对象逼近的临界增益值 b0 提供合理的估计值。为此,可采用以下方法。
- 使用幅值为 uOL 的阶跃信号,在工作范围内对开环被控对象进行仿真。
- 记录较短持续时间内被控对象输出的变化。
- 对于一阶 ADRC,请使用响应逼近 y = at 并确定 a,如下所示。
a = y ( e n d ) − y ( 0 ) t ( e n d ) − t ( 0 ) a=\dfrac{y(e n d)-y(0)}{t(e n d)-t(0)} a=t(end)−t(0)y(end)−y(0) - 对于二阶 ADRC,请使用响应逼近 y = ½at² 并确定 a,如下所示。
a = 2 ( y ( e n d ) − y ( 0 ) ) ( t ( e n d ) − t ( 0 ) ) 2 a={\dfrac{2(y(e n d)-y(0))}{(t(e n d)-t(0))^{2}}} a=(t(end)−t(0))22(y(end)−y(0))
- 对于一阶 ADRC,请使用响应逼近 y = at 并确定 a,如下所示。
- 然后,您可以基于 a 和阶跃幅值 uOL 确定 b0。
b 0 = a u O L b{\mathrm{{0}}}={\dfrac{a}{u O L}} b0=uOLa
在模块参数中使用临界增益参数设置此值。
然后,要调节控制器响应,请分别使用控制器带宽和观测器带宽指定 ωc 和 ωo 值。这些值取决于控制器的性能要求。一般情况下,更快的响应需要更大的控制器带宽。观测器还需要比控制器收敛得更快。因此,请将观测器带宽设置为控制器带宽的 5 到 10 倍。
此外,该模块允许您指定状态的初始条件,限制控制器输出,并输出估计的状态值。
参考
[1] Han, Jingqing. “From PID to Active Disturbance Rejection Control.” IEEE Transactions on Industrial Electronics 56, no. 3 (March 2009): 900–906. https://doi.org/10.1109/TIE.2008.2011621.
[2] Herbst, Gernot. “A Simulative Study on Active Disturbance Rejection Control (ADRC) as a Control Tool for Practitioners.” Electronics 2, no. 3 (August 15, 2013): 246–79. https://doi.org/10.3390/electronics2030246.
[3] Zhiqiang Gao. “Scaling and Bandwidth-Parameterization Based Controller Tuning.” In Proceedings of the 2003 American Control Conference, 2003, 6:4989–96. Denver, CO, USA: IEEE, 2003. https://doi.org/10.1109/ACC.2003.1242516.