1. 前序和中序遍历

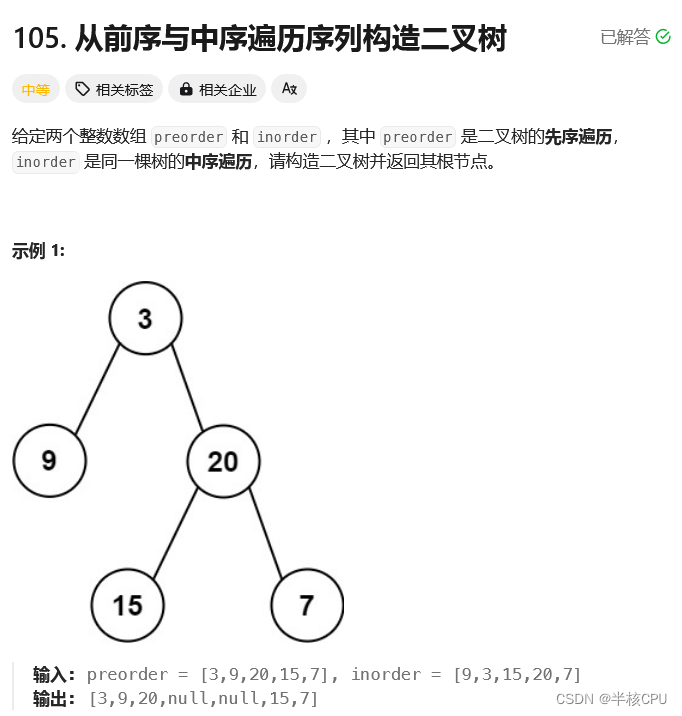
**思路：我们每一次一定可以根据递归确定根节点是哪个，就是前序第一个数，然后找中序遍历这个点，看左子树有几个节点，右子树有几个节点，然后就可以根据节点个数，递归左子树和右子树，当且仅当left>right时结束，由于preorder和inorder对应的所以left>right只需要判断一个符不符合就行了。**8个位置的判断一定要仔细。借助hashmap确定中序遍历某个节点的位置。

class Solution {
    Map<Integer,Integer> mp = new HashMap();
    int n;
    TreeNode PreMidTreeBuilder(int[] preorder,int[] inorder,
            int preorder_left, int preorder_right, int inorder_left, int inorder_right){
        if(preorder_left>preorder_right) return null;
        TreeNode root = new TreeNode(0,null,null);
        int rootNodeVal = preorder[preorder_left];
        root.val = rootNodeVal;
        //定位到中序遍历的位置
        int inorderRoot = mp.get(rootNodeVal);
        //可以根据坐标定下来左右子树的节点数量
        int leftLength = inorderRoot-inorder_left;
        int rightLength = inorder_right-inorderRoot;
        root.left=
            PreMidTreeBuilder(preorder,inorder,preorder_left+1,preorder_left+leftLength,
                            inorder_left,inorderRoot-1);    
        root.right=
            PreMidTreeBuilder(preorder,inorder,preorder_left+leftLength+1,preorder_right,
                            inorderRoot+1,inorder_right);
        return root;
    }
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        n = preorder.length;
        for(int i=0;i<n;i++)
            mp.put(inorder[i],i);
        return PreMidTreeBuilder(preorder,inorder,0,n-1,0,n-1);
    }
}

2. 中序和后序遍历

和前序+中序完全一样的思路，可以说所有这种题都是这个思路。

class Solution { 
    Map<Integer,Integer> map = new HashMap<>();
    public TreeNode buildInPostTree(int[] inorder, int[] postorder,
                    int inorder_left,int inorder_right,int postorder_left,int postorder_right)
    {
        if(inorder_left>inorder_right)return null;
        int val = postorder[postorder_right];
        int inorder_root = map.get(val);
        int nums_left_tree = inorder_root-inorder_left;
        int nums_right_tree = inorder_right-inorder_root;
        TreeNode root = new TreeNode(val,null,null);
        root.left = buildInPostTree(inorder,postorder,inorder_left,inorder_left+nums_left_tree-1,
                                    postorder_left,postorder_left+nums_left_tree-1);
        root.right = buildInPostTree(inorder,postorder,inorder_root+1,inorder_right,
                                    postorder_right-nums_right_tree,postorder_right-1);
        return root; 
    }
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        int n = inorder.length;
        for(int i=0;i<n;i++)
            map.put(inorder[i],i);
        return buildInPostTree(inorder,postorder,0,n-1,0,n-1);
    }
}