学习目标:
动态规划五部曲:
① 确定dp[i]的含义
② 求递推公式
③ dp数组如何初始化
④ 确定遍历顺序
⑤ 打印递归数组 ---- 调试
引用自代码随想录!
60天训练营打卡计划!
学习内容:
343. 整数拆分
- 动态规划五步曲:
① 确定dp[i]的含义 : 对i拆分后 得最大乘积为dp[i]
② 求递推公式 :
Ⅰ j * dp[i - j] ,其中dp[i - j]代表两个数及以上的最大乘积。我根本不需要关心dp[i - j]是怎么组成的,因为题目只要求求出拆分后的最大的乘积,并没有问什么样的拆分结果可以获取拆分后的最大乘积。
Ⅱ j * (i - j) 代表拆为两个数,两个数的乘积
Ⅲ 所以 dp[i] = max(j * dp[i - j] , j * (i - j) , dp[i]) ---- 因为dp[i]代表的是拆分后的最大的乘积,所以一定是从既有的dp[i] 结果以及有潜在可能性有最大值的结果中取出最大值。
③ dp数组如何初始化 : dp[0] = 0 dp[1] = 0 dp[2] = 1
④ 确定遍历顺序 : 从前向后 - 在实现的过程中还有一些小的技巧,比如说拆分的时候只需要使j 遍历到 i/2 的位置即可,最大值一定会落到这个范围中来。
class Solution {
public int integerBreak(int n) {
// 申请空间时一定要多申请一位!
int[] dp = new int[n + 1];
dp[0] = 0;
dp[1] = 0;
dp[2] = 1;
if(n == 2) return dp[n];
// dp数组的值依赖所求项的前n-1项,故需要逐个求解dp数组的值。
for(int i = 3; i <= n; i++){
for(int j = 0; j <= i/2; j++){
dp[i] = Math.max(j * dp[i - j], j * (i - j)) > dp[i] ?
Math.max(j * dp[i - j], j * (i - j)) : dp[i];
}
}
return dp[n];
}
}
96.不同的二叉搜索树
-
二叉搜索树:使用中序遍历可以得到一个递增的有序数组。
-
需要画出1 2 3三种情况中二叉搜索树的情况,要观察递推公式。
dp[3] = dp[0]*dp[2] +dp[1]*dp[1]+dp[2]*dp[0] -
动态规划五步曲:
① 确定dp[i]的含义 : 第i个数可以构造出的二叉搜索树的个数。
② 求递推公式 : dp[i] = dp[j-1]*dp[i-j] ( j 从 1 增到 i ,求和 )
③ dp数组如何初始化 : dp[0] = 1 dp[1] = 1 dp[2] = 2 dp[3] = 5
④ 确定遍历顺序 : 从小向大
// 动态规划
class Solution {
public int numTrees(int n) {
int[] dp = new int[n+1];
// dp[0]一定是1
dp[0] = 1;
dp[1] = 1;
if(n == 1) return dp[n];
dp[2] = 2;
if(n == 2) return dp[n];
for(int i = 3; i <= n; i++){
for(int j = 1; j <= i; j++){
dp[i] += dp[j-1] * dp[i-j];
}
// System.out.println(dp[i]);
}
return dp[n];
}
}
二维数组处理01背包问题
- 听起来思路很简单,但其实一点也不好实现。
- 动态规划五步曲:
① 确定dp[i][j]的含义 : 任取[0, i]的物品后放进容量为j的背包 所能放的 最大价值
② 求递推公式 : dp[i][j] = max(dp[i-1][j] , dp[i-1][ j - weight[i] ] + value[i])
Ⅰ 不放物品 i : dp[i-1][j]
Ⅱ 放物品 i : dp[i-1][j - weight[i]] + value[i]
③ dp数组如何初始化 : 按下表的第一行和第一列赋值,其中箭头都是继承来的值,画圈的表示自己取得了最大值。
④ 确定遍历顺序 : 先物品后背包(行) / 先背包后物品(列)
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
//m,n分别代表物品种类和背包容量
int itemSize = 0,bagSize = 0;
Scanner sc = new Scanner(System.in);
//获取itemSize和bagSize的值
itemSize = sc.nextInt();
bagSize = sc.nextInt();
//初始化对应的重量数组和价值数组
int[] weight = new int[itemSize];
int[] value = new int[itemSize];
//这两个都是物品的属性,大小只和物品数量有关
for(int i = 0;i < itemSize;i++){
weight[i] = sc.nextInt();
}
for (int i = 0;i < itemSize;i++){
value[i] = sc.nextInt();
}
// int[] weight = {1,3,4};
// int[] value = {15,20,30};
// int bagSize = 4;
testWeightBagProblem(weight,value,bagSize);
}
/**
* 动态规划获得结果
* @param weight 物品的重量
* @param value 物品的价值
* @param bagSize 背包的容量
*/
public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){
// 创建dp数组
int goods = weight.length; // 获取物品的数量
int[][] dp = new int[goods][bagSize + 1];
// 初始化dp数组
// 创建数组后,其中默认的值就是0
// 只有当背包放得下物品时,才能附该物品的价值
for (int j = weight[0]; j <= bagSize; j++) {
dp[0][j] = value[0];
}
// 填充dp数组
for (int i = 1; i < goods; i++) {
for (int j = 1; j <= bagSize; j++) {
// 防止越界错误
if (j < weight[i]) {
dp[i][j] = dp[i-1][j];
} else {
dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);
}
}
}
System.out.print(dp[goods-1][bagSize]);
// 打印dp数组
// System.out.print(dp[goods-1][bagSize] + "\n");
// for (int i = 0; i < goods; i++) {
// for (int j = 0; j <= bagSize; j++) {
// System.out.print(dp[i][j] + "\t");
// }
// System.out.println("\n");
// }
}
}
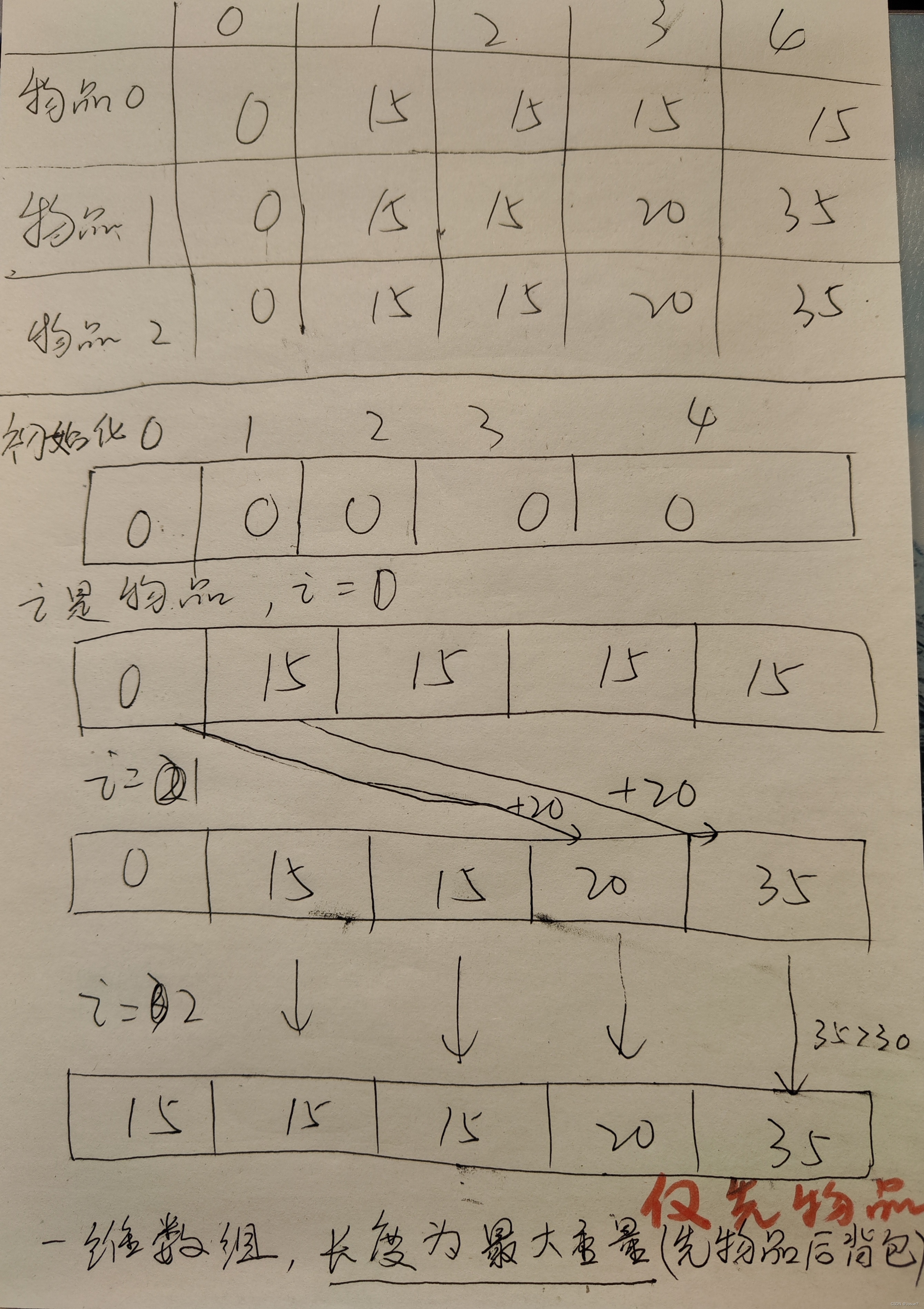
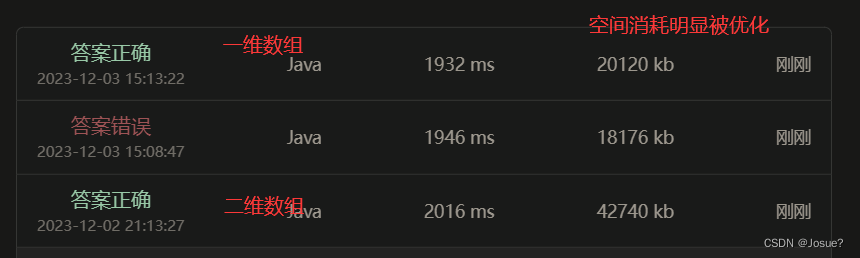
一维数组处理01背包问题
- 动态规划五步曲:
① 确定dp[j]的含义 : 任取物品放进容量为j的背包 所能放的 最大价值
② 求递推公式 : dp[j] = max(dp[j] , dp[j - weight[i]] + value[i])
Ⅰ 不放物品 i : dp[j]
Ⅱ 放物品 i : dp[j - weight[i]] + value[i]
③ dp数组如何初始化 : 初始值全部附0,长度为容量的长度加1(j+1)
④ 确定遍历顺序 : 必须先物品后背包(行),且便利背包大小时,必须使用倒序的顺序遍历。(为了防止一个物品被使用多次,倒叙遍历时相同的物品仅能被取用一次)
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
//m,n分别代表物品种类和背包容量
int itemSize = 0,bagSize = 0;
Scanner sc = new Scanner(System.in);
//获取itemSize和bagSize的值
itemSize = sc.nextInt();
bagSize = sc.nextInt();
//初始化对应的重量数组和价值数组
int[] weight = new int[itemSize];
int[] value = new int[itemSize];
//这两个都是物品的属性,大小只和物品数量有关
for(int i = 0;i < itemSize;i++){
weight[i] = sc.nextInt();
}
for (int i = 0;i < itemSize;i++){
value[i] = sc.nextInt();
}
// int[] weight = {1,3,4};
// int[] value = {15,20,30};
// int bagSize = 4;
testWeightBagProblem(weight,value,bagSize);
}
/**
* 动态规划获得结果
* @param weight 物品的重量
* @param value 物品的价值
* @param bagSize 背包的容量
*/
public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){
// 创建dp一维数组
int goods = weight.length; // 获取物品的数量
int[] dp = new int[bagSize + 1];
// 初始化dp数组
// 创建数组后,其中默认的值就是0
// 填充dp数组
for (int i = 0; i < goods; i++) {
// 必须使用倒叙遍历背包大小
for (int j = bagSize; j > 0; j--) {
// 防止越界错误
if (j < weight[i]) {
dp[j] = dp[j];
} else {
dp[j] = Math.max(dp[j] , dp[j-weight[i]] + value[i]);
}
}
}
System.out.print(dp[bagSize]);
// 打印dp数组
// System.out.print(dp[goods-1][bagSize] + "\n");
// for (int i = 0; i < goods; i++) {
// for (int j = 0; j <= bagSize; j++) {
// System.out.print(dp[i][j] + "\t");
// }
// System.out.println("\n");
// }
}
}
学习时间:
- 上午两个半小时,整理文档半小时。