二叉树的实现
定义结构体
我们首先定义一个结构来存放二叉树的节点
结构体里分别存放左子节点和右子节点以及节点存放的数据
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
构造一个二叉树
我们首先定义一个新建新节点的函数,方便构造二叉树
BTNode* buynode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc");
return NULL;
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}
然后就是构造二叉树之间的节点关系和节点中存储的元素
这里我们构造的是一个满二叉树,各个节点关系如下图所示
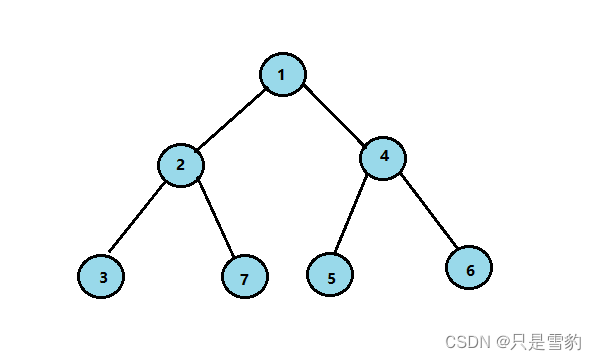
BTNode* createtree()
{
BTNode* node1 = buynode(1);
BTNode* node2 = buynode(2);
BTNode* node3 = buynode(3);
BTNode* node4 = buynode(4);
BTNode* node5 = buynode(5);
BTNode* node6 = buynode(6);
BTNode* node7 = buynode(7);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
node2->right= node7;//满二叉树
return node1;
}
返回二叉树节点个数
这里有两种方法:
一种是遇到空节点直接返回,否则size++,然后再递归使用左节点和右节点,这种方法就做计数
第二种是直接递归使用左节点加右节点+1,这种方法更加简洁,但是可读性没有第一种方法这么好
int BinaryTreeSize(BTNode* root)
{
//static size = 0;
//if (root == NULL)
// return;
//size++;
//BinaryTreeSize(root->left);
//BinaryTreeSize(root->right);
//return size;
if (root == NULL)
return 0;
return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
返回二叉树叶子节点个数
叶子节点就是没有孩子,即左节点和右节点都为空
当根节点root为空时直接返回0,当左节点left和右节点right都为空是就返回1,然后递归root的左节点和右节点相加,最后返回的就是叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
返回二叉树第k层节点个数
这里的二叉树根节点是第一层
首先k必须大于0,进行断言
如果根节点为空就直接返回0
如果k为1,就只有根节点一个节点,返回1
再递归左子树的k-1和右子树的k-1层节点数相加就是第k层的节点数
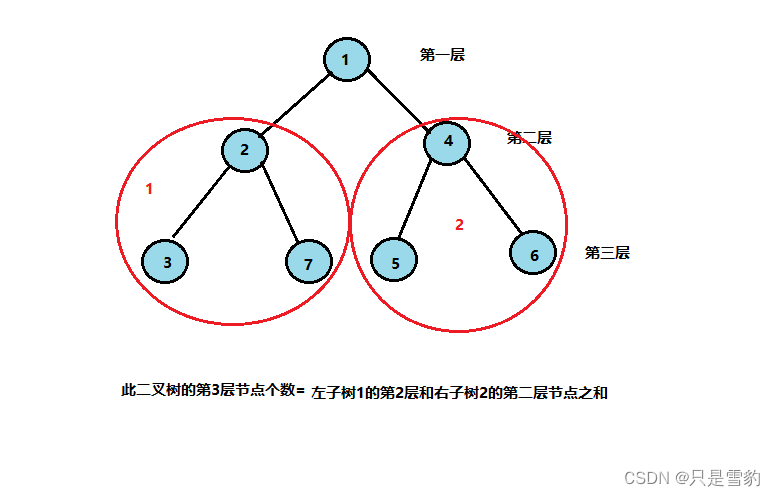
int BinaryTreeLevelKSize(BTNode* root, int k)
{
assert(k > 0);
if (root == NULL)
return 0;
if (k == 1)
return 1;
return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
二叉树查找值为x的节点
查找节点其实大家都有误区
例如:
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
BinaryTreeFind(root->left, x);
BinaryTreeFind(root->right, x);
}
但是这种情况下如果没有这个节点怎么办呢
所以这是错误滴
正确的在下面:
我们申请空间分别存放递归后左节点和右节点的返回值,如果不为空就返回
如果到最后还没有返回值就是二叉树中没有这个节点,直接返回空
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
BTNode* node1 = BinaryTreeFind(root->left, x);
if (node1)
return node1;
BTNode* node2 = BinaryTreeFind(root->right, x);
if (node2)
return node2;
return NULL;
}
二叉树的销毁
很简单,但是记得手动置空
void BinaryTreeDestory(BTNode* root)
{
if (root == NULL)
return;
BinaryTreeDestory(root->left);
BinaryTreeDestory(root->right);
free(root);//为了防止出现野指针,需要使用者自己手动置空,即root==Null
}
求二叉树的高度
其实而二叉树的高度就是层数,我们只要计算层数最多的分支即可
如果左子树大于右子树就返回左子树的递归结果+1,右子树反之
大家看一下下面这段代码
int BinaryTreeHeight(BTNode* root)
{
if (root == NULL)
return 0;
return BinaryTreeHeight(root->left) > BinaryTreeHeight(root->right) ? BinaryTreeHeight(root->left) + 1 : BinaryTreeHeight(root->right) + 1;
}
上面这段代码是有问题的,他没有将其记录下来,就回返回很多次去查询数据,导致超出时间限制
下面这段代码给出了解决的办法
记录即可
int BinaryTreeHeight(BTNode* root)
{
if (root == NULL)
return 0;
int leftheight = BinaryTreeHeight(root->left);
int rightheight = BinaryTreeHeight(root->right);
return leftheight > rightheight ? leftheight + 1 : rightheight+1;
}
二叉树的遍历
前序、中序以及后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
- 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
前序、中序以及后序遍历的实现
这三个遍历很简单,难得是层序遍历
前序就是先访问根节点,然后左子树右子树,用递归解决即可
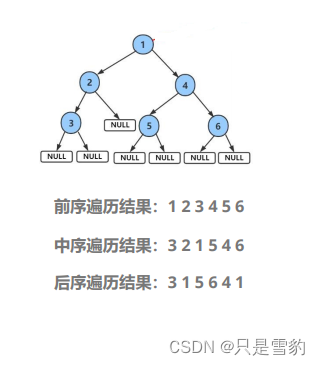
前序
void BinaryTreePrevOrder(BTNode* root)
{
if (root)
{
putchar(root->_data);
BinaryTreePrevOrder(root->_left);
BinaryTreePrevOrder(root->_right);
}
}
中序
void BinaryTreeInOrder(BTNode* root)
{
if (root)
{
BinaryTreeInOrder(root->_left);
putchar(root->_data);
BinaryTreeInOrder(root->_right);
}
}
后序
void BinaryTreePostOrder(BTNode* root)
{
if (root)
{
BinaryTreePostOrder(root->_left);
BinaryTreePostOrder(root->_right);
putchar(root->_data);
}
}
层序遍历的实现
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
看图理解即可:
访问顺序是
A B C D E F G
层序遍历得实现其实要用到队列:
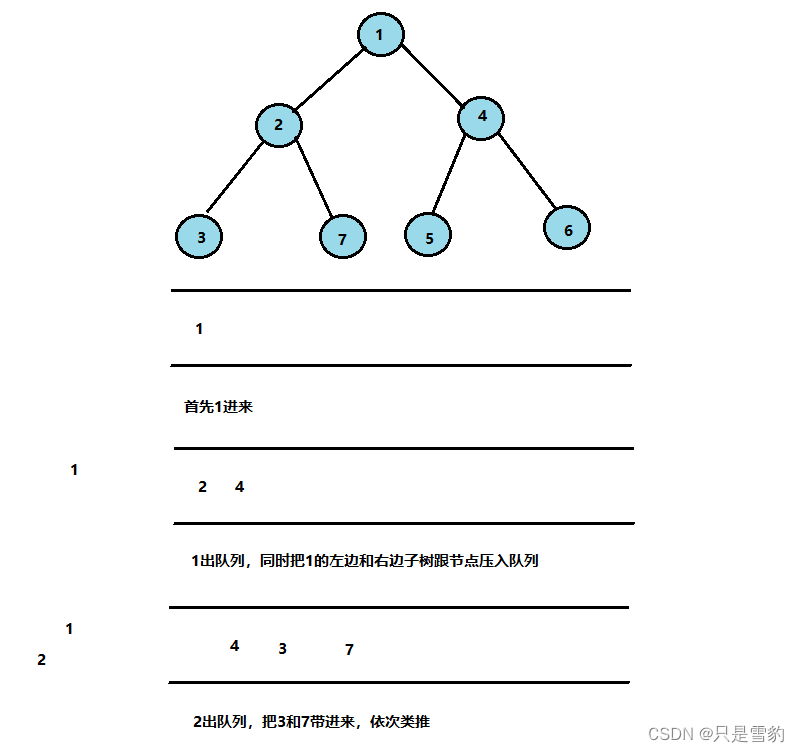
上图给了一个解释,大家可以研究研究
void BinaryTreeLevelOrder(BTNode* root)
{
Queue qu;
BTNode * cur;
QueueInit(&qu);
//首先压入根节点
QueuePush(&qu, root);
//循环的终止条件就是当队列为空时,此时二叉树层序遍历完成
while (!QueueIsEmpty(&qu))
{
//第一次进入循环时cur为队列的队首,即根节点
cur = QueueTop(&qu);
putchar(cur->data);
//当cur的左不为空是入队列
if (cur->left)
{
QueuePush(&qu, cur->left);
}
//当cur的右不为空是入队列
if (cur->right)
{
QueuePush(&qu, cur->right);
}
//删除此时的队首元素,并返回打印
QueuePop(&qu);
}
QueueDestory(&qu);
}
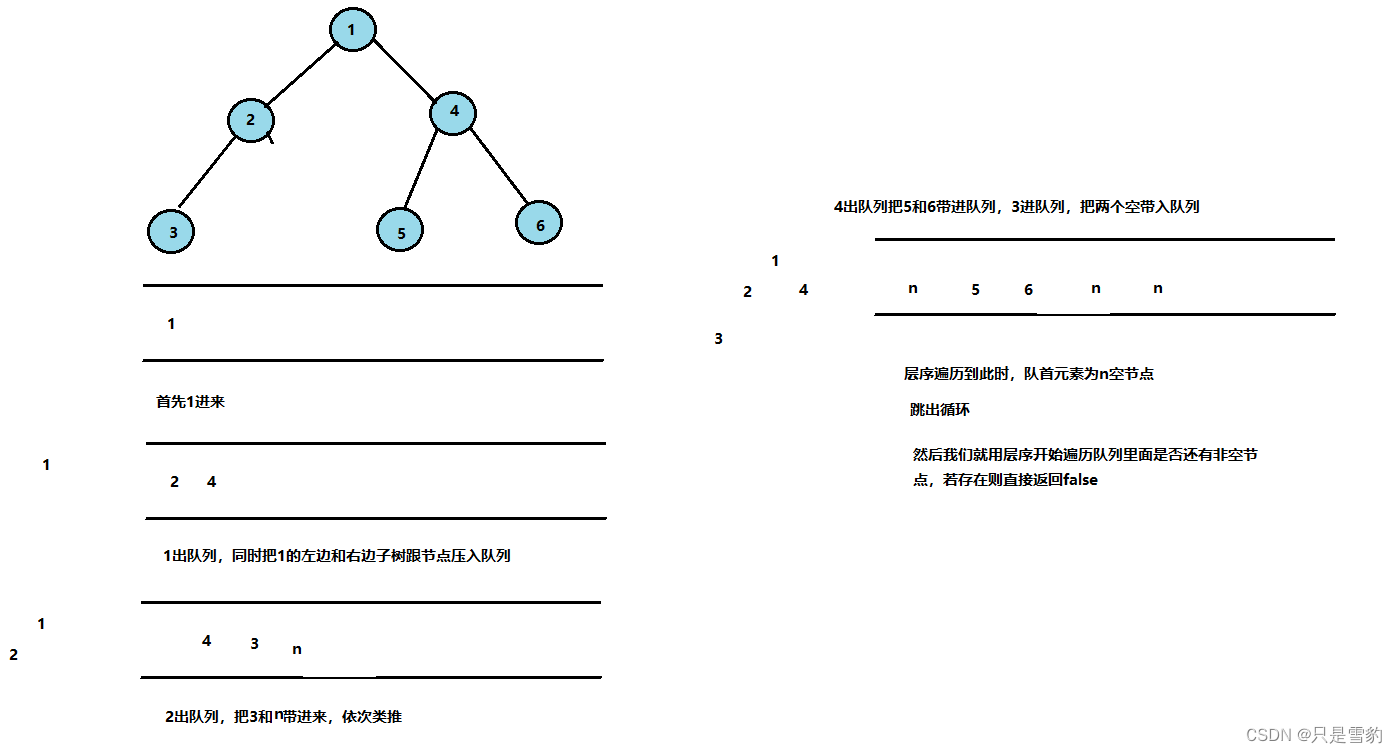
二叉树是否为完全二叉树
判断是否未完全二叉树的条件是什么呢
就是层序遍历完成时中间有无空节点!
我们首先将根节点压入队列
然后再将队列队首元素删除返回后,判断队首元素是否为空,为空则跳出while循环,就当他是个完全二叉树的所有节点已经全部压入
如果不是空就将左子树和右子树的根节点压入
然后我们再用层序遍历来判断后面是否有非空节点,如果有的话就不是完全二叉树,return false
否则是完全二叉树
看图分析即可:
bool BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)//遇空就跳出
break;
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
//检查后面是否有非空节点,有非空就是非完全二叉树
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}
好了,本文到此结束,感谢大家的支持!