题目1:198 打家劫舍
题目链接:打家劫舍
对题目的理解
专业小偷偷盗房屋的钱财,每个房屋存放的金额用非负整数数组表示;
如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警;
不触动警报装置的情况下,一夜之内能偷窃的最高金额;
当前房屋偷与不偷取决于前一个房屋和前两个房屋是否被偷了。即当前状态和前面状态会有一种依赖关系,那么这种依赖关系都是动规的递推公式,打家劫舍是dp解决的经典问题
动规五部曲
1)dp数组及下标i的含义
dp[i]:考虑下标i(包含下标i)之前的房间所能偷的最大的金币为dp[i]
最终结果:dp[nums[i]-1]
2)递推公式
决定dp[i]的因素就是第i个房间偷还是不偷
偷房间i的金币:dp[i]=dp[i-2]+nums[i],第i-1个房一定是不考虑的,找出下标i-2(包括i-2)以内的房屋
不偷房间i的金币:dp[i]=dp[i-1],考虑i-1房,(注意这里是考虑,并不是一定要偷i-1房)
dp[i]=max(dp[i-2]+nums[i],dp[i-1])
3)dp数组初始化
根据递推公式看出,dp[0]和dp[1]是递推公式的基础,所以初始化为dp[0]=nums[0],dp[1]=max(nums[0],nums[1]),其余非0下标,初i始成任意值均可,因为dp[i]是从前面两个得到的,最终会被计算的结果覆盖
4)遍历顺序
i要从小到大百遍历,这样才能使用前面的值推导后面的dp[i]
for(i=2;i<nums.size();i++)
5)打印dp数组
代码
class Solution {
public:
int rob(vector<int>& nums) {
//定义并初始化dp数组
vector<int> dp(nums.size(),0);
if(nums.size()==0) return 0;
if(nums.size()==1) return nums[0];
dp[0]=nums[0];
dp[1]=max(nums[0],nums[1]);
//递推
for(int i=2;i<nums.size();i++){
dp[i]=max(dp[i-2]+nums[i],dp[i-1]);
}
return dp[nums.size()-1];
}
};- 时间复杂度: O(n)
- 空间复杂度: O(n)
题目2:213 打家劫舍Ⅱ
题目链接:打家劫舍Ⅱ
对题目的理解
房屋围成一圈,最后一个房屋和第一个房屋时紧挨着的,如果两间相邻的房屋在同一晚上被闯入,系统会自动报警,在不触动报警装置的情况下,偷窃到的最高金额
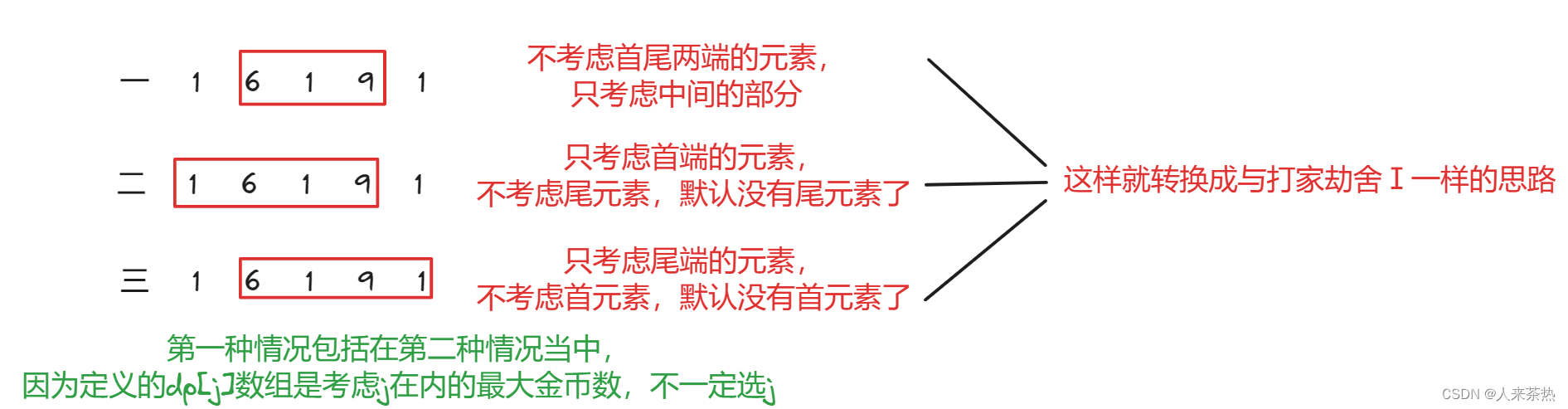
将环形问题转换为线性问题,因为最后一个房间和第一个房间是挨着的,所以进行分类讨论,考虑3种情况,!!!用的是"考虑",例如情况三,虽然是考虑包含尾元素,但不一定要选尾部元素!
动规五部曲
1)dp数组及下标初始化
dp[i]:考虑下标i(包含下标i)之前的房屋所能盗窃的最大金币数
2)递推公式
与打家劫舍Ⅰ的递推公式相同dp[i]=max(dp[i-1],dp[i-2]+nums[i]),只不过最终比较考虑首端元素的情况与考虑尾端元素的情况的最大值
3)dp数组初始化
与打家劫舍Ⅰ的初始化相同,dp[0]=nums[0],dp[1]=max(nums[0],nums[1])
4)遍历顺序
从小到大遍历
5)打印dp数组
将打家劫舍Ⅰ的代码封装成函数,然后比较首端和尾端取值的最大值
代码
class Solution {
public:
int robrange(vector<int>nums,int begin,int end){
if(end==begin) return nums[begin];
//定义并初始化dp数组
vector<int> dp(nums.size(),0);
dp[begin]=nums[begin];
dp[begin+1]=max(nums[begin],nums[begin+1]);
//递推
for(int i=begin+2;i<=end;i++){
dp[i]=max(dp[i-2]+nums[i],dp[i-1]);
}
return dp[end];
}
int rob(vector<int>& nums) {
if(nums.size()==0) return 0;
if(nums.size()==1) return nums[0];
int result1 = robrange(nums,0,nums.size()-2);//只考虑首端元素
int result2 = robrange(nums,1,nums.size()-1);//只考虑尾端元素
return max(result1, result2);
}
};- 时间复杂度: O(n)
- 空间复杂度: O(n)
题目3:337 打家劫舍Ⅲ
题目链接:打家劫舍Ⅲ
对题目的理解
房子是二叉树的形式,两个直接相连的放在在同一晚被打劫,就会报警,返回不报警的最大金额
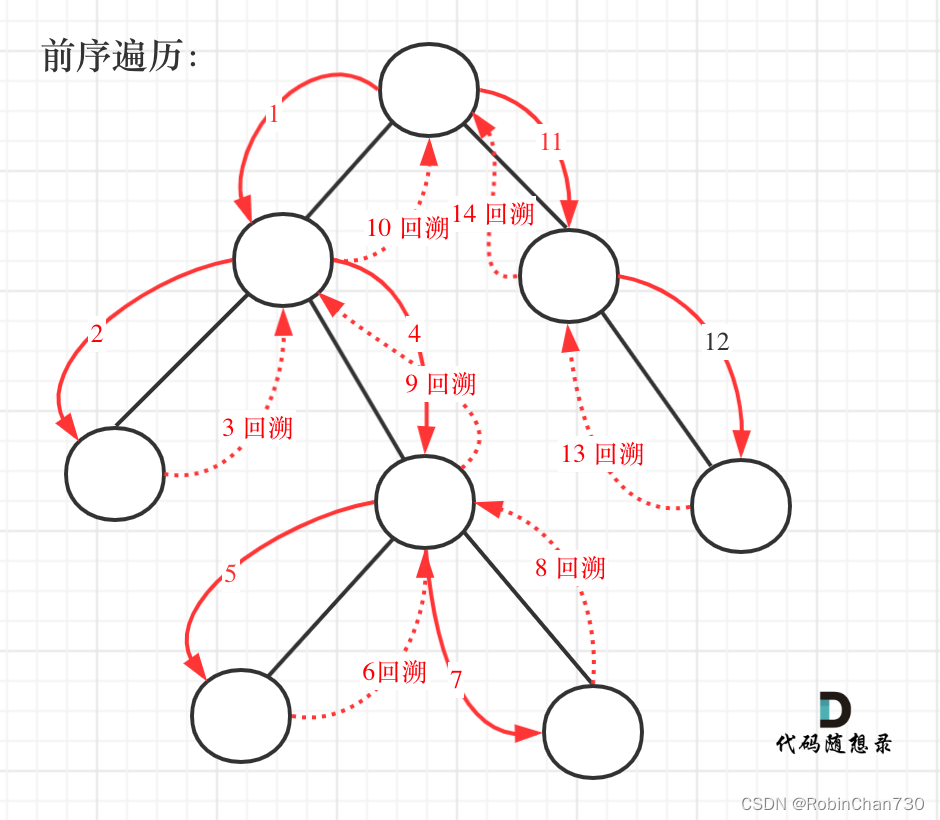
本题一定是要后序遍历,因为通过递归函数的返回值来做下一步计算。
与打家劫舍,打家劫舍II一样,关键是要讨论当前节点抢还是不抢。
如果抢了当前节点,两个孩子就不能动,如果没抢当前节点,就可以考虑抢左右孩子(注意这里说的是“考虑”)
暴力搜索法
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int rob(TreeNode* root) {
if(root==NULL) return 0;
if(root->left==NULL && root->right==NULL) return root->val;
//偷父节点
int val1=root->val;
if(root->left) val1+=rob(root->left->left)+rob(root->left->right);
if(root->right) val1+=rob(root->right->left)+rob(root->right->right);
//不偷父节点
int val2 = rob(root->left)+rob(root->right);
return max(val1,val2);
}
};- 时间复杂度:O(n^2),这个时间复杂度不太标准,也不容易准确化,例如越往下的节点重复计算次数就越多
- 空间复杂度:O(log n),算上递推系统栈的空间
以上代码超时了,这个递归的过程中其实是有重复计算了,计算了root的四个孙子(左右孩子的孩子)为头结点的子树的情况,又计算了root的左右孩子为头结点的子树的情况,计算左右孩子的时候其实又把孙子计算了一遍。

记忆化递推
使用一个map把计算过的结果保存一下,这样如果计算过孙子了,那么计算孩子的时候可以复用孙子节点的结果。
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
unordered_map<TreeNode*,int> umap;//记录计算过的结果
int rob(TreeNode* root) {
if(root==NULL) return 0;
if(root->left==NULL && root->right==NULL) return root->val;
if(umap[root]) return umap[root];
//偷父节点
int val1=root->val;
if(root->left) val1+=rob(root->left->left)+rob(root->left->right);
if(root->right) val1+=rob(root->right->left)+rob(root->right->right);
//不偷父节点
int val2 = rob(root->left)+rob(root->right);
umap[root]=max(val1,val2);
return max(val1,val2);
}
};- 时间复杂度:O(n)
- 空间复杂度:O(log n),算上递推系统栈的空间
动态规划
在上面两种方法,其实对一个节点 偷与不偷得到的最大金钱都没有做记录,而是需要实时计算
树形dp的入门题目,因为是在树上进行状态转移,以递归三部曲为框架,其中融合动规五部曲
递归三部曲
1)确定递归函数的参数和返回值
求一个节点 偷与不偷的两个状态所得到的金钱,那么返回值就是一个长度为2的数组,返回的数组就是dp数组
dp数组以及下标的含义:下标为0记录不偷该节点所得到的的最大金钱,下标为1记录偷该节点所得到的的最大金钱,使用一个长度为2的数组,记录当前节点偷与不偷所得到的的最大金钱。
在递归的过程中,系统栈会保存每一层递归的参数
2)确定终止条件
在遍历的过程中,如果遇到空节点的话,很明显,无论偷还是不偷都是0,所以就返回,相当于dp数组的初始化
3)确定遍历顺序
使用后序遍历。 因为要通过递归函数的返回值来做下一步计算。
通过递归左节点,得到左节点偷与不偷的金钱。
通过递归右节点,得到右节点偷与不偷的金钱。
4)确定单层递归逻辑
如果是偷当前节点,那么左右孩子就不能偷,val1 = cur->val + left[0] + right[0];
如果不偷当前节点,那么左右孩子就可以偷,至于到底偷不偷一定是选一个最大的,所以:val2 = max(left[0], left[1]) + max(right[0], right[1]);
最后当前节点的状态就是{val2, val1}; 即:{不偷当前节点得到的最大金钱,偷当前节点得到的最大金钱},注意顺序不能颠倒,因为递归逻辑里面就是偷与不偷,不偷在前,偷在后
5)打印dp数组
最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱。
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int rob(TreeNode* root) {
//定义并初始化dp数组
vector<int> dp=robtree(root);
return max(dp[0],dp[1]);
}
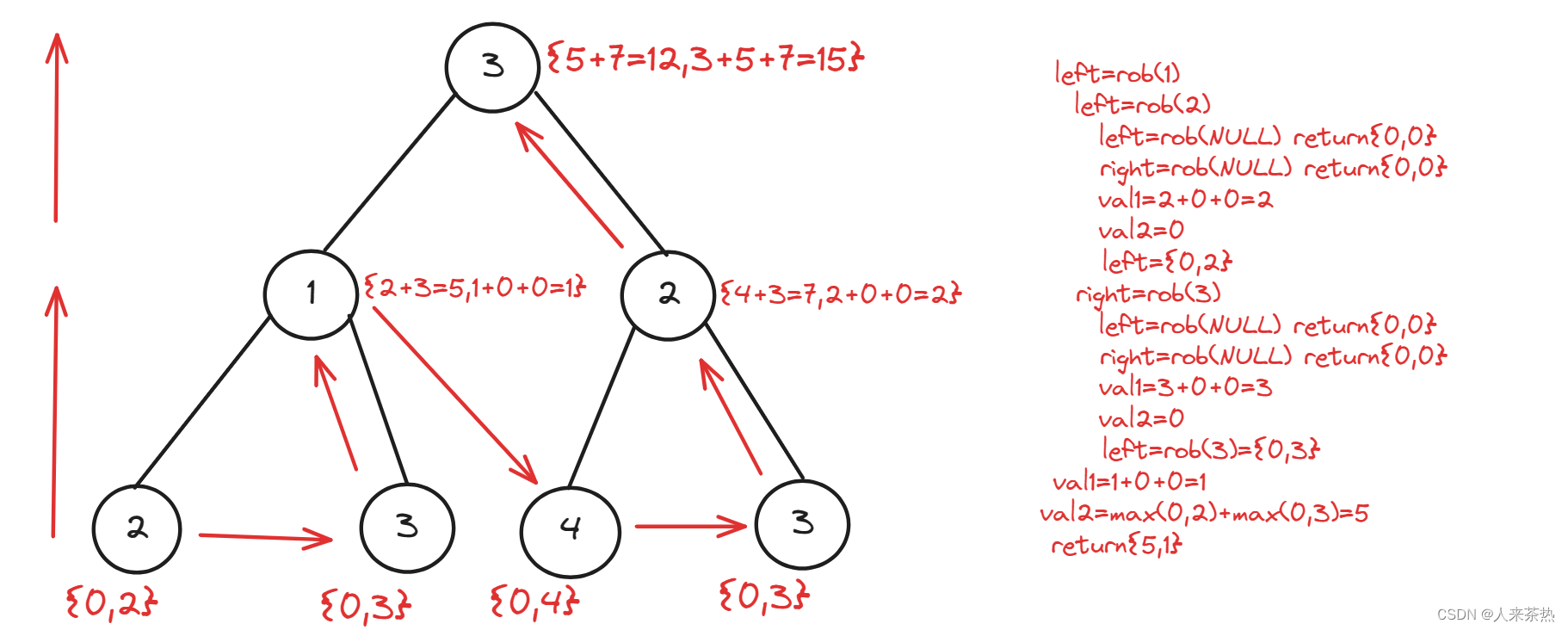
vector<int> robtree(TreeNode* cur){
if(cur==NULL) return vector<int>{0,0};//偷和不偷两个状态
vector<int> left=robtree(cur->left);//左孩子
vector<int> right=robtree(cur->right);//右孩子
//偷cur
int val1=cur->val+left[0]+right[0];
//不偷kur
int val2=max(left[0],left[1])+max(right[0],right[1]);
return {val2,val1};//注意这里返回的顺序不要弄反,因为每一层递归需要这个顺序的返回值
}
};- 时间复杂度:O(n),每个节点只遍历了一次
- 空间复杂度:O(log n),算上递推系统栈的空间