1、介绍

        细分方法是从任意多边形网格生成平滑曲面的简单而强大的方法。与基于样条曲面的方法（如NURBS）或其他基于数字的建模技术不同，细分方法的使用者不需要掌握细分方法的数学知识。几何的直观性足以控制细分方法。

        Subdivision_method_3适用于Polyhedron_3和Surface_mesh类，因为它们是MutatableFaceGraph概念的模型，并且旨在易于使用和扩展。 Subdivision_method_3不是一个类，而是一个包含四种流行细分方法及其细化函数的命名空间。 这些方法包括Catmull-Clark、Loop、Doo-Sabin和3-√细分。 通过替换细化规则的几何计算，可以很容易地扩展这些方法的变体。

2、细分方法

       在拓扑学中，流形是局部具有欧几里得空间性质的空间。如果一个拓扑空间是可微的，那么它就是一个流形。如果一个流形只有有限个不相交的连通组件，那么它就是一个流形。2-流形是一个二维的流形。

        在本章中，我们解释了细分方法的一些基本原理。我们只关注那些有助于你理解这个包的设计的主题。本节中介绍的一些术语将在后面的章节中再次使用。

        细分方法递归细化粗糙网格，并生成与光滑曲面越来越接近的近似值。粗糙网格可以有任意形状，但它必须是2-流形。在2-流形中，每个内部点都有一个与2D圆盘同胚的邻域。非流形上的细分方法已经开发出来，但在Subdivision_method_3中没有考虑。本章的预告片展示了CAD模型上Catmull-Clark细分的步骤。粗糙网格通过四分模式反复细化，并生成新点以近似光滑曲面。

        实践中使用了许多细分模式。 Subdivision_method_3支持四种最流行的模式，每种模式都由Catmull-Clark、Loop、Doo-Sabin和3-√细分（下图从左到右）使用。我们根据拓扑特征而不是相关的细分方法来命名这些模式。PQQ表示原始四边形四等分。PTQ表示原始三角形四等分。DQQ表示对偶四边形四等分。3-√表示三角剖分向细分曲面的收敛速度。

        这个图表展示了这四种细分模式的应用，下面的源网格展示了细分的网格。细分网格上的点是通过平均源网格上的相邻点来生成的。一个称为模板的图形决定了源邻域，该邻域的点有助于确定细分点的位置。细分模式通常定义了多个模板。例如，PQQ细分具有一个顶点模板，它定义了输入顶点的1-ring；一个边模板，它定义了输入边的1-ring；以及一个面模板，它定义了输入面。PQQ细分的模板在下图中显示。顶部的蓝色区域表示红色细分节点的相应模板。 

        带权重的模板被称为几何掩码。细分方法为每个模板定义一个几何掩码，并通过加权掩码的源点平均值来生成新点。几何掩码是精心选择的，以满足特定表面平滑度和形状质量的要求。Catmull-Clark细分方法的几何掩码如下所示。 

 

        此处显示的权重未标准化，n是顶点的权重。生成的点（红色）是通过加权点的求和计算出来的。例如，Catmull-Clark面节点是通过其模板上每个点的1/4求和计算出来的。

        模板可以具有无限数量的几何掩模。例如，PQQ细分的面节点可以通过每个模板节点的1/5的总和来计算，而不是1/4。虽然在Subdivision_method_3中可以使用任何类型的几何掩模，但结果表面可能是奇数、不光滑或甚至不存在的。 

3、Catmull-Clark细分

Subdivision_method_3::CatmullClark_subdivision(pmesh, params::number_of_iterations(d));

        subdivision_method_3 指定细分函数的名称空间。 CatmullClark_subdivision(P, params::number_of_iterations(d)) 计算多边形网格 pmesh 在 d 次细化迭代后的 Catmull-Clark 细分曲面。 多边形网格 pmesh 通过引用传递，并由细分函数修改（即细分）。

       应用程序定义的多边形网格可能使用专门的内核和/或专门的内部容器。使用 Subdivision_method_3 的应用程序定义的多边形网格有一个主要限制：内部容器中的基元（如顶点、半边和面）是按顺序排列的（例如 std::vector 和 std::list）。这意味着迭代器按创建/插入顺序遍历基元。

        Subdivision_method_3 旨在允许对细分方法进行定制。下面该实现演示了将 PQQ 细化定制到 Catmull-Clark 细分。

        开发细分方法时，选择细化模式，然后开发一组几何掩模来定位新点。实现细分方法有三个关键组成部分：能够表示任意2流形的网格数据结构，一种优化网格数据结构的过程，以及计算新点的几何权重。

        下面选择了PQQ细化作为他们的细分方法，并开发了一套几何掩模，用于从控制网格生成（或更精确地近似）B样条曲面。 Subdivision_method_3提供了一个函数，可以粘合Catmull-Clark细分方法的所有三个组件。

template <class PolygonMesh, class Mask, class NamedParameters>
void PQQ(PolygonMesh& p, Mask mask, NamedParameters np)

        PolygonMesh 必须是 Polyhedron_3、Surface_mesh 或 MutableFaceGraph 概念的其他模型的实例。它是用于任意二维流形的通用网格数据结构。PQQ() 是一个细化的控制网格 p，它使用策略类 Mask<PolygonMesh> 作为其几何计算的一部分。在细化过程中，PQQ() 通过与掩模合作来计算和分配新点。要实现 Catmull-Clark 细分，掩模、几何策略必须实现 Catmull-Clark 细分的几何掩模。迭代次数和顶点映射可以使用命名参数 np 指定。

        为了实现几何掩模，我们需要知道细化主体如何与其几何掩模进行通信。PQQ细化定义了三个模板，因此Catmull-Clark细分需要三个几何掩模。以下类定义了PQQ细化的模板接口。 

template <class PolygonMesh>
class PQQMask_3 {
  void face_node(boost::graph_traits<PolygonMesh>::face_descriptor face, Point_3& pt);
  void edge_node(boost::graph_traits<PolygonMesh>::halfedge_descriptor edge, Point_3& pt);
  void vertex_node(boost::graph_traits<PolygonMesh>::vertex_descriptor vertex, Point_3& pt);
};

         PQQMask_3中的每个类函数都根据基元描述符的邻域计算一个新的点，并将该新点分配给Point_3& pt。

        我们使用Catmull-Clark细分的几何掩模来实现每个类函数。

        要调用 Catmull-Clark 细分方法，我们使用刚刚定义的 Catmull-Clark 掩码调用 PQQ()。

PQQ(pmesh, CatmullClark_mask_3(pmesh), params::number_of_iterations(depth));

        Loop、Doo-Sabin 和 3-√ 分段使用类似的过程实现：选择一个细化宿主并实现几何策略。开发自己的细分方法的关键是实现细化宿主和几何策略的正确组合。

4、细分主体

        细化主体是多边形网格类和几何体遮罩类的模板函数。它细化输入多边形网格，并通过几何体遮罩计算新点。Subdivision_method_3支持四个细化主体：原始四边形四边形（PQQ）、原始三角形四边形（PTQ）、对偶四边形四边形状（DQQ）和3–√三角测细化。分别由Catmull Clark、Loop、Doo Sabin和3–√细分使用。

        mesh类必须是MutatableFaceGraph的模型，它必须是三角形网格或多边形网格，而mask是一个实现细分方法的几何掩模的策略类。

        细化主体细化输入多边形网格，维护模板（即控制网格和细化网格之间的映射），并调用几何权重来计算新点。在 Subdivision_method_3 中，细化是通过一系列连接操作（主要是欧拉操作）实现的。连接操作的顺序在维护模板时起着关键作用。通过将源子网格的顺序与细化顶点相匹配，不需要在基元中标记模板。这避免了细化主体对多边形网格类的数据依赖。

        为了使排序技巧起作用，多边形网格类必须有一个顺序容器，如向量或链表，作为内部存储。顺序容器保证多边形网格的迭代器始终按插入顺序遍历基元。非顺序结构不提供所需的顺序，因此不能与 Subdivision_method_3 一起使用。

        虽然 Subdivision_method_3 不需要标记来支持细化和模板，但它仍然需要知道如何计算和存储几何数据（即点）。 Subdivision_method_3 的类有一个可选的模板参数，即一个顶点属性映射，它提供了顶点和点之间的映射。

        细分主体 PQQ 和 DQQ 在普通多边形网格上工作，PTQ 和 Sqrt3 在三角化多边形网格上工作。 PTQ 和 Sqrt3 在非三角化多边形网格上的结果未定义。 Subdivision_method_3 在细分之前不验证网格特性的先决条件。

5、几何策略

        几何策略定义了一组几何权重。每个几何掩码都实现为计算细分曲面新点的成员函数。

        每个几何掩模接收控制网格的图元描述符（例如 halfedge_descriptor），并向细分的顶点返回 Point_3。该函数收集图元描述符的顶点邻居（即模板上的节点），并根据邻居和掩模（即模板权重）计算新点。

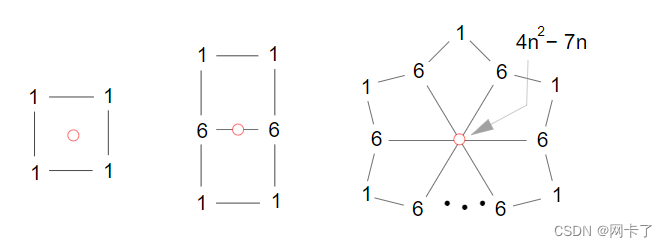
        此图显示了 Catmull-Clark 细分的几何掩码。此处显示的权重未标准化，n 是顶点的化合价。新点是通过在其模板上加权点的总和来计算的。以下代码显示了面节点的几何掩码的实现。

template <class PolygonMesh, class VertexPointMap>
class CatmullClark_mask_3 {
  typedef boost::graph_traits<PolygonMesh>::face_descriptor face_descriptor;
  typedef boost::property_traits<VertexPointMap>::value_type Point_3;
  CatmullClark_mask_3(PolygonMesh &pmesh, VertexPointMap vpm);
  void face_node(face_descriptor face, Point_3& pt) {
    int n = 0;
    Point_3 p(0,0,0);
    for(halfedge_descriptor hd : halfedges_around_face(face,pmesh)){
      p = p + get(vpm, (target(hd,pmesh)) - ORIGIN);
      ++n;
    }
    pt = ORIGIN + (p - ORIGIN)/FT(n);
  }
};

        Catmull-Clark细分的细化主体需要三个几何掩码，用于没有开放边界的多边形网格：顶点节点掩码、边节点掩码和面节点掩码。为了支持有边界的多边形网格，还需要边界节点掩码。Catmull-Clark细分的边界节点掩码如下，其中ept返回新的点分割边，vpt返回边指向的顶点上的新点。 

        下面列出了所有四个细化主体的掩模接口。 DQQMask_3 没有边界节点模板，因为 DQQ 细化的细化主机在当前版本中不支持全局边界。

template <class PolygonMesh>
class PQQMask_3 {
  void face_node(boost::graph_traits<PolygonMesh>::face_descriptor, Point_3&);
  void edge_node(boost::graph_traits<PolygonMesh>::halfedge_descriptor, Point_3&);
  void vertex_node(boost::graph_traits<PolygonMesh>::vertex_descriptor, Point_3&);
  void border_node(boost::graph_traits<PolygonMesh>::halfedge_descriptor, Point_3&, Point_3&);
};
template <class PolygonMesh>
class PTQMask_3 {
  void edge_node(boost::graph_traits<PolygonMesh>::halfedge_descriptor, Point_3&);
  void vertex_node(boost::graph_traits<PolygonMesh>::vertex_descriptor, Point_3&);
  void border_node(boost::graph_traits<PolygonMesh>::halfedge_descriptor, Point_3&, Point_3_&);
};
template <class PolygonMesh>
class DQQMask_3 {
public:
  void corner_node(boost::graph_traits<PolygonMesh>::halfedge_descriptor edge, Point_3& pt);
};
template <class PolygonMesh>
class Sqrt3Mask_3 {
public:
  void vertex_node(boost::graph_traits<PolygonMesh>::vertex_descriptor vertex, Point_3& pt);
};

6、四种细分方法

        Subdivision_method_3 通过专门化其各自的细化规则来支持 Catmull-Clark、Loop、Doo-Sabin 和 3-√ 细分。它们旨在用于 MutableFaceGraph 的任何模型，如 Polyhedron_3 和 Surface_mesh。如果您的应用程序使用具有专用几何内核的多边形网格，则需要使用基于该内核的几何策略来专门化细化规则。

namespace Subdivision_method_3 {
  template <class PolygonMesh, class NamedParameters>
  void CatmullClark_subdivision(PolygonMesh& pmesh, NamedParameters np) {
    PQQ(pmesh, CatmullClark_mask_3<PolygonMesh>(pmesh), np);
  }
  template <class PolygonMesh, class NamedParameters>
  void Loop_subdivision(PolygonMesh& pmesh, NamedParameters np) {
    PTQ(pmesh, Loop_mask_3<PolygonMesh>(pmesh) , np);
  }
  template <class PolygonMesh, class NamedParameters>
  void DooSabin_subdivision(PolygonMesh& pmesh, NamedParameters np) {
    DQQ(pmesh, DooSabin_mask_3<PolygonMesh>(pmesh), np);
  }
  template <class PolygonMesh, class NamedParameters>
  void Sqrt3_subdivision(PolygonMesh& pmesh, NamedParameters np) {
    Sqrt3(pmesh, Sqrt3_mask_3<PolygonMesh>(pmesh), np);
  }
}

7、自定义细分方法

        Subdivision_method_3 支持在具有笛卡尔坐标点的 Polyhedron_3 上使用四种实用的细分方法。通过使用自定义几何掩模对细化规则进行专门化，可以支持更多的细分方法。

        有四个已经定义好的细分方法，还有四个接受几何掩膜的细分主体。

CGAL 5.6 - 3D Surface Subdivision Methods: User Manual