高级算法设计与分析练习1-10

文章目录

7-1 锦标赛
7-2 选我啊！
7-3 朋友圈
7-4 最短路径
7-5 ICPC保定站
7-6 填数字
7-7 Werewolf
7-8 球队“食物链”
7-9 代码排版
7-10 至多删三个字符

7-1 锦标赛

HBU有2 n名ACM选手，编号依次为1−2 n。他们现在要进行一场程序设计比赛，这个比赛最终只会有一个获胜者。
第i名选手的cf rating为ai ，保证任意两名选手的cf rating均不相同，两名选手进行比赛的话，一定是cf rating高的一方获胜。
这场锦标赛看起来就像一个完全二叉树，形式化的描述如下：
第1名选手将会和第2名选手进行比赛，第3名选手将会和第4名选手进行比赛，⋯ ，第2 n−1名选手和第2 n名选手进行比赛。
第1名和第2名中获胜的那名选手将会和第3名选手和第4名选手中获胜进行比赛，以此类推，直到比赛结束。
现在请你求出，在最后一轮比赛中，输的那名选手的编号是多少？

输入格式
第一行输入一个正整数，代表n。
第二行，2 n 个正整数，代表每名选手的cf rating。
1≤n≤16
1≤a i≤10 9
保证a i 均不相同
输出格式
输出在最后一场比赛中输那名选手的编号

#include <iostream>
#include <vector>
#include<algorithm>
#include <queue>
using namespace std;

int findLoser(int n, vector<int>& ratings) {
    int numOfPlayers = 1 << n;
    queue<int> players; // 使用队列存储选手编号

    // 初始化选手编号
    for (int i = 1; i <= numOfPlayers; ++i) {
        players.push(i);
    }

    // 模拟比赛过程
    while (players.size() > 1) {
        int size = players.size();
        for (int i = 0; i < size; i += 2) {
            int first = players.front();
            players.pop();
            if (i + 1 < size) {
                int second = players.front();
                players.pop();
                if (size == 2)
                    swap(ratings[first], ratings[second]);
                // 比赛并将赢得比赛的选手放回队列中
                if (ratings[first] < ratings[second]) {
                    players.push(second);
                }
                else {
                    players.push(first);
                }
            }
            else {
                players.push(first);
            }
        }
    }
    // 最后一轮bug
    return players.front(); // 返回输掉比赛的选手编号
}

int main() {
    int n;
    cin >> n;

    int numOfPlayers = 1 << n;
    vector<int> ratings(numOfPlayers + 1);

    // 读取选手的 cf rating
    for (int i = 1; i <= numOfPlayers; ++i) {
        cin >> ratings[i];
    }

    int loserId = findLoser(n, ratings);
    cout << loserId << endl;

    return 0;
}

7-2 选我啊！

HBU最近在进行花美男的选举，候选人是A同学和B同学。
HBU一共有n个学院，其中第i个学院有a i 名同学支持A同学，b i名同学支持B同学。
但是，B同学可以在每个学院发表演讲来获得更多的同学对他的支持。
如果B同学在某个学院进行了一场演讲，那么这个学院的全部同学都会支持他，包括原来支持A同学的那些同学。
相反，如果B同学不在某个学院发表演讲，那么这个学院中原来支持A同学的那些同学还会支持A同学，但是那些原来支持B同学的同学们将不再支持B同学，他们会变的中立——谁也不支持。
请你求出B同学最少在几个学院发表演讲才能让支持他的同学人数超过支持A同学的人数。

输入格式
第一行一个正整数n。后面n行，每行两个正整数(a i ,b i )，分别代表第i个学院中支持A同学的人数和支持B同学的人数。
1≤n≤2×10 5 1 ≤a i ,b i≤10 9
输出格式
请输出答案

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2e5 + 10;
struct stu {
    LL a, b, c;
}st[N];
 
LL resa;
int n;
bool cmp(stu s1, stu s2) {
    return s1.c > s2.c;
}
int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i++) {
        scanf("%d%d", &st[i].a, &st[i].b);
        resa += st[i].a;
        st[i].c = st[i].a * 2 + st[i].b;
    }
    sort(st, st + n, cmp);
    int res = 0;
    for (int i = 0; i < n; i++) {
        if (resa < 0)break;
        resa -= st[i].c;
        res++;
    }
    cout << res;
 
    return 0;
}

7-3 朋友圈

#include <iostream>
#include <unordered_map>
using namespace std;

typedef long long LL;
const int N = 200010, mod = 1e9 + 7;
int n, q, x;
int a, b, c;
int p[N];
unordered_map<int, int> res[N];
int siz[N];

int find(int x) {
    if (x != p[x]) p[x] = find(p[x]);
    return p[x];
}

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    
    cin >> n >> q;
    for (int i = 1; i <= n; i++) {
        siz[i] = 1;
        cin >> x;
        res[i][x]++;
        p[i] = i;
    }

    while (q--) {
        cin >> c >> a >> b;
        if (c == 1) {
            a = find(a), b = find(b);
            if (a != b) {
                if (siz[a] > siz[b]) {
                    p[b] = a;
                    siz[a] += siz[b];
                    for (auto& it : res[b]) {
                        res[a][it.first] += it.second;
                    }
                } else {
                    p[a] = b;
                    siz[b] += siz[a];
                    for (auto& it : res[a]) {
                        res[b][it.first] += it.second;
                    }
                }
            }
        } else {
            a = find(a);
            cout << res[a][b] << "\n";
        }
    }
    return 0;
}

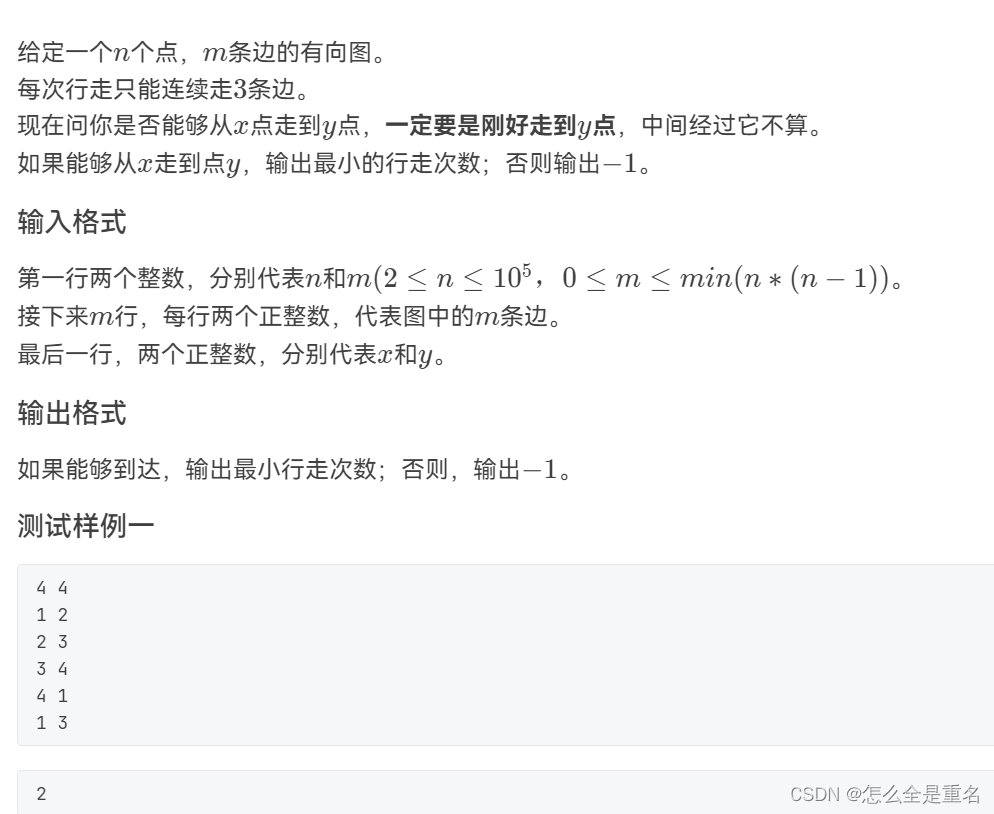
7-4 最短路径

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

const int MAX_NODES = 100001; // 最大节点数
vector<int> graph[MAX_NODES]; // 图的邻接表表示

int BFS(int start, int end) {
    queue<pair<int, int>> q; // 队列保存节点和步数
    vector<vector<int>> visited(MAX_NODES, vector<int>(4, false)); // 记录节点是否被访问过，同时记录步数

    q.push({start, 0}); // 从起点开始，步数为0
    visited[start][0] = true; // 标记起点为已访问，步数为0

    while (!q.empty()) {
        int node = q.front().first;
        int steps = q.front().second;
        q.pop();

        if (node == end && steps % 3 == 0 && steps != 0) {
            return steps / 3; // 找到终点，返回步数/3
        }

        // 扩展当前节点的所有相邻节点
        for (int i = 0; i < graph[node].size(); ++i) {
            int nextNode = graph[node][i];

            if (!visited[nextNode][(steps + 1) % 3]) {
                visited[nextNode][(steps + 1) % 3] = true;
                q.push({nextNode, steps + 1});
            }
        }
    }

    return -1; // 未找到符合条件的路径
}

int main() {
    int n, m;
    cin >> n >> m;

    for (int i = 0; i < m; ++i) {
        int u, v;
        cin >> u >> v;
        graph[u].push_back(v); // 构建有向图的邻接表
    }

    int x, y;
    cin >> x >> y;

    int minSteps = BFS(x, y);

    cout << minSteps << endl;

    return 0;
}

7-5 ICPC保定站

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 50;
typedef pair<int, int> PII;
int n, t, k;
int w[N];
LL weights[1 << 24], cnt = 0;
LL res;
 
void dfs1(int u, LL s) {
    if (u == k) {
        weights[cnt++] = s;
        return;
    }
 
    dfs1(u + 1, s);
    if (s + w[u] <= t)dfs1(u + 1, s + w[u]);
}
 
void dfs2(int u, LL s) {
    if (u == n) {
        int l = 0, r = cnt - 1;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (weights[mid] <= (LL)t - s)l = mid;
            else r = mid - 1;
        }
        if (weights[l] + s <= t)
            res = max(res, weights[l] + s);
        return;
    }
 
    dfs2(u + 1, s);
    if (w[u] + s <= t)dfs2(u + 1, s + w[u]);
}
 
 
int main()
{
    scanf("%d%d", &n, &t);
    for (int i = 0; i < n; i++)scanf("%d", &w[i]);
 
    sort(w, w + n);
    reverse(w, w + n);
 
    k = n / 2;
 
    dfs1(0, 0);
 
    sort(weights, weights + cnt);
    cnt = unique(weights, weights + cnt) - weights;
    dfs2(k, 0);
 
    cout << res;
    return 0;
}

7-6 填数字

#include <iostream>
#include <string>
using namespace std;

const int MOD = 1e9 + 7;

int countWays(string s) {
    int dp[13] = {1};

    for (char c : s) {
        int temp[13] = {0};

        if (c == '?') {
            for (int i = 0; i <= 9; ++i) {
                for (int j = 0; j < 13; ++j) {
                    temp[(j * 10 + i) % 13] = (temp[(j * 10 + i) % 13] + dp[j]) % MOD;
                }
            }
        } else {
            int digit = c - '0';
            for (int j = 0; j < 13; ++j) {
                temp[(j * 10 + digit) % 13] = dp[j];
            }
        }

        for (int i = 0; i < 13; ++i) {
            dp[i] = temp[i];
        }
    }

    return dp[5];
}

int main() {
    string s;
    cin >> s;

    int ways = countWays(s);
    cout << ways << endl;

    return 0;
}

7-7 Werewolf

就是PAT甲里面的狼人杀

#include <bits/stdc++.h>
using namespace std;
int n, m, L, record[105];
bool iswolf[105] = {0}, flag = false; //分别存放该玩家是否是狼，以及是否已经找到符合条件的情况 
std::vector<int> ans, tempans;
//判断谎言家是否满足要求 
bool isTrue(){
	int cntL = 0, cntM_L = 0;
	for(int i = 1; i <= n; ++ i){
		if((iswolf[abs(record[i])] && record[i] > 0) || (!iswolf[abs(record[i])] && record[i] < 0)){
			++ cntL;
			if(iswolf[i])
				++ cntM_L; 
		}
	}
	return cntL == L && cntM_L != m && cntM_L > 0;
}
void dfs(int index){
	if(flag)
		return;
	if(index == 0 && tempans.size() == m){
		if(isTrue()){
			flag = true;
			ans = tempans;
		}
		return;
	}
	if(tempans.size() > m || index == 0)
		return;
	for(int i = index; i > 0; -- i){
		tempans.push_back(i);
		iswolf[i] = 1;
		dfs(i-1);
		iswolf[i] = 0;
		tempans.pop_back();
		dfs(i-1);
	}
}
int main(){
	scanf("%d %d %d", &n, &m, &L);
	for(int i = 1; i <= n; ++ i)
		scanf("%d", &record[i]);
	dfs(n);
	if(!flag)
		printf("No Solution\n");
	else{
		printf("%d", ans[0]);
		for(int i = 1; i < ans.size(); ++ i)
			printf(" %d", ans[i]);
	}
}

7-8 球队“食物链”

//注意：i战胜j可以是st[i][j]='W'||st[j][i]='L';
#include<stdio.h>
#include<string.h>
int n;
char st[25][25];
int a[25];
int ans;
int l;
int visit[25];
int u;
void dfs(int v)
{
	int i,j;
	if(ans==1)
	return ;
	if(l==n)
	{
		if(st[v][u]=='W'||st[u][v]=='L')
		{
			for(j=0;j<n-1;j++)
			printf("%d ",a[j]+1);
			printf("%d\n",a[n-1]+1);
			ans=1;
			return ;
		}
	}
	for(i=0;i<n;i++)
	{
		if(ans==1)
		return ;
		int tag=0;
		//优化,因为是一个环,若该点没有战胜0,则就没有必要对该点判断下去 
		for(j=1;j<n;j++)
		{
			if(!visit[j]&&st[j][0]=='W'||st[0][j]=='L')
			{
				tag=1;
				break;
			}
		}
		if(tag==0)
		return ;
		if(!visit[i]&&(st[v][i]=='W'||st[i][v]=='L'))
		{
			visit[i]=1;
			a[l]=i;
			l++;
			dfs(i);
		    visit[i]=0;
		    l--;
		}	
	}
}
int main()
{
	int i,j;
	scanf("%d",&n);
	for(i=0;i<n;i++)
	scanf("%s",st[i]);
	int tag=0;
	//优化,因为是一个环,所以若存在一个食物链,就直接判断从0开始是否可以即可 
	for(i=1;i<n;i++)
	{
		if(st[i][0]=='W'||st[0][i]=='L')
		{
			tag=1;
			break;
		}
	}
	if(tag==0)
	{
		printf("No Solution\n");
		return 0;
	}
	memset(visit,0,sizeof(visit));
    ans=0;
	l=0;
	u=0;
	a[l]=0;
	l++;
	visit[0]=1;
	dfs(0);
	if(ans==0)
	printf("No Solution\n");
	return 0;
}

7-9 代码排版

某编程大赛中设计有一个挑战环节，选手可以查看其他选手的代码，发现错误后，提交一组测试数据将对手挑落马下。为了减小被挑战的几率，有些选手会故意将代码写得很难看懂，比如把所有回车去掉，提交所有内容都在一行的程序，令挑战者望而生畏。

为了对付这种选手，现请你编写一个代码排版程序，将写成一行的程序重新排版。当然要写一个完美的排版程序可太难了，这里只简单地要求处理C语言里的for、while、if-else这三种特殊结构，而将其他所有句子都当成顺序执行的语句处理。输出的要求如下：

默认程序起始没有缩进；每一级缩进是 2 个空格；
每行开头除了规定的缩进空格外，不输出多余的空格；
顺序执行的程序体是以分号“;”结尾的，遇到分号就换行；
在一对大括号“{”和“}”中的程序体输出时，两端的大括号单独占一行，内部程序体每行加一级缩进，即：

{
  程序体
}

for的格式为：

for (条件) {
  程序体
}

while的格式为：

while (条件) {
  程序体
}

if-else的格式为：

if (条件) {
  程序体
}
else {
  程序体
}

输入格式：
输入在一行中给出不超过 331 个字符的非空字符串，以回车结束。题目保证输入的是一个语法正确、可以正常编译运行的 main 函数模块。

输出格式：
按题面要求的格式，输出排版后的程序

#include <bits/stdc++.h>
using namespace std;
int point, space = 2, mark, tp, cnt, use, temp;
string s;
int Function(int c) {
	if (c == 0) while (s[point] == ' ') point++;
	else if (c == 1) for (int i = 0; i < space; i++) cout << ' ';
	else if (c == 2) {
		if (s.substr(point, 2) == "if" && (s[point + 2] == '(' || s[point + 2] == ' ')) return 2;
		else if (s.substr(point, 3) == "for" && (s[point + 3] == '(' || s[point + 3] == ' ')) return 3;
		else if (s.substr(point, 4) == "else" && (s[point + 4] == '(' || s[point + 4] == ' ')) return 4;
		else if (s.substr(point, 5) == "while" && (s[point + 5] == '(' || s[point + 5] == ' ')) return 5;
	} else if (c == 3) {
		Function(0);
		if (Function(2) == 4) return 0;
		while (mark) {
			space -= 2;
			Function(1);
			cout << "}\n";
            mark--;
		} 
	}
	return 0;
}
int main() {
	getline(cin, s);
	Function(0);
	for (int i = point; s[i] != ')'; i++) cout << s[i];
	cout << ")\n{\n";
	point = s.find('{') + 1;
	while (1) {
		Function(0);
		temp = Function(2);
		if (s[point] == '{') {
			Function(1);
			cout << "{\n";
			space += 2;
			point++;
		} else if (s[point] == '}') {
			space -= 2;
			Function(1);
			cout << "}\n";
			if (space == 0) return 0;
			Function(3);
			point++;
		} else if (temp) {
			Function(1);
			cout << s.substr(point, temp);
			point += temp;
			if (temp != 4) {
				Function(0);
				tp = point;
				cnt = 0;
				while(tp < s.size()) {
					if (s[tp] == '(') cnt++;
					else if (s[tp] == ')') cnt--;
					tp++;
					if (cnt == 0) break;
				}
				cout << ' ' << s.substr(point, tp - point);
				point = tp;
			}
			cout <<  " {\n";
			space += 2;
			Function(0);
			if (s[point] != '{') {
				use = 1;
				mark++;
			} else {
				use = 0;
				point++;
			}
		} else {
			Function(1);
			cnt = s.find(';', point);
			cout << s.substr(point, cnt - point + 1) << '\n';
			point = cnt + 1;
			if (use && mark) {
				space -= 2;
				Function(1);
				cout << "}\n";
				mark--;
				Function(3);
			}
		}
	}
	return 0;
}

7-10 至多删三个字符

给定一个全部由小写英文字母组成的字符串，允许你至多删掉其中 3 个字符，结果可能有多少种不同的字符串？

输入格式：输入在一行中给出全部由小写英文字母组成的、长度在区间 [4, 10 6 ] 内的字符串。

输出格式：在一行中输出至多删掉其中 3 个字符后不同字符串的个数。

输入样例： ababcc
输出样例： 25
提示：
删掉 0 个字符得到 “ababcc”。
删掉 1 个字符得到 “babcc”, “aabcc”, “abbcc”, “abacc” 和 “ababc”。
删掉 2 个字符得到 “abcc”, “bbcc”, “bacc”, “babc”, “aacc”, “aabc”, “abbc”, “abac” 和 “abab”。
删掉 3 个字符得到 “abc”, “bcc”, “acc”, “bbc”, “bac”, “bab”, “aac”, “aab”, “abb” 和 “aba”

#include<bits/stdc++.h>
#define PII pair<int,int>
#define x first
#define y second
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int N = 1e6 + 7;
using namespace std;

char s[N];
ll dp[N][4];
int main(int argc, char const *argv[])
{
    scanf("%s", s + 1);
    int len = strlen(s + 1);
    dp[0][0] = 1;   //递推入口
    for (int i = 1; i <= len; i++)
    {
        for (int j = 0; j < 4; j++)
        {
            if (i < j)break;   //如果不够删，肯定跳出啊
            dp[i][j] = dp[i - 1][j];   //不删第i个，
            if (j >= 1)dp[i][j] += dp[i - 1][j - 1];//删除第i个
            for (int k = i - 1; k >= 1 && i - k <= j; k--)  //上面操作肯定有重的，这里来去重
            {    //逐一查找前面的，，，，但这个过程中删除的数也不能超出j个啊
                //i-k==j代表，从第k个到第i-1个全部删了的操作
                if (s[k] == s[i])  //找到相等的了
                {                   //那么这个相等的数肯定要删掉，所以是i-k<=j
                    dp[i][j] -= dp[k - 1][j - (i - k)];  //找第k个前面的，然后找还剩余能删几个
                    break;   //找到第一个重复的点，这是k最大的时候，也是剩余能删k前面最多的时候
                }              //这个时候就不用往前找了，因为这里就包括了前面的
            }
        }
    }
    ll ans = 0;
    for (int i = 0; i <= 3; i++)  //把4种都加起来
    {
        ans += dp[len][i];
    }
    printf("%lld\n", ans);

    return 0;
}