直流电(DC)电机由于其转矩易于控制,速度控制范围广,已广泛应用于可调速驱动或可变转矩控制中。然而,直流电机有一个主要的缺点,即它们需要机械装置,如换向器和刷子来连续旋转。这些机械部件需要定期维护,并阻碍了高速运行。最近,由于交流(AC)电机控制技术、电力电子技术和微处理器的重大发展,交流电机代替直流电机,但直流电机仍在低额定功率在几千瓦以下使用。
在本章中,我们将研究直流电机的电流和速度控制。了解直流电机的当前控制技术和速度控制技术是非常重要的,因为这些技术直接适用于交流电机的控制,这将在第6章中讨论。
直流电动机的配置
一个直流电机有两个绕组,如图2.1所示。一个在定子中被发现,并产生一个场通量。这种绕组被称为场绕组。另一个位于转子中,被称为电枢绕组。电枢电流与定子磁场通量相互作用,在转子轴上产生扭矩。小型直流电动机通常有一个永磁体,而不是一个磁场绕组来产生定子磁通。直流电动机还具有由电刷和换向器组成的机械换向装置,它将由直流电源给出的直流电流转换为电枢绕组中的交流电流。

直流电机主要可分为两类:分别励磁直流电机和自励磁直流电机。在单独励磁的直流电动机中,电枢绕组和现场绕组各有单独的直流电源,而在自励的直流电动机中,两个绕组共用一个直流电源。
根据自励绕组与直流电源的连接方式,自励直流电动机也可分为并联电机、串联电动机和复合电动机。现在的直流电机主要使用永磁体产生的磁场通量和直流电源因此仅适用于电枢绕组。
现在我们将了解电刷和换向器的作用,这是直流电机的连续旋转必不可少的。首先,我们将看看图2.2,它显示了一个转子绕组中的一圈线圈。当线圈连接到直流电源时,电流流过线圈。我们假设,在初始阶段,通量分布和电流在线圈中形成的左图。在这种情况下,两侧导体上的力使线圈根据弗莱明左手法则给出的力的方向顺时针方向旋转。

当线圈旋转并到达右图中所示的位置时,在两侧的导体上产生的力将使线圈再次回到如图2.2左侧所示的初始位置。由于在线圈上产生的力不是在一个方向上连续产生的,
线圈也不能在同一方向上连续旋转。然而,当线圈在右边所示的位置时,如果电流的方向相反,那么在两侧导体上产生的力就会相反,因此,线圈上的力将保持在顺时针方向。这样,线圈就会沿着这个方向连续地旋转。通过电刷和换向器的换向作用,线圈电流可以反转,如图2.3所示。应注意的是,流过线圈的电流必须是直流电机中的交流电。这种交流电的频率总是与线圈的角速度相同,这表示转子的速度。在第1.2.3节中,我们已经看到,这满足了在双馈电机器中连续产生扭矩的必要条件。

直流电机的电枢绕组有多个线圈,可以增加平均转矩,减小转矩波纹波,如图2.4所示。每个线圈通过一个刷子和它自己的隔离换向器连接到直流电源。
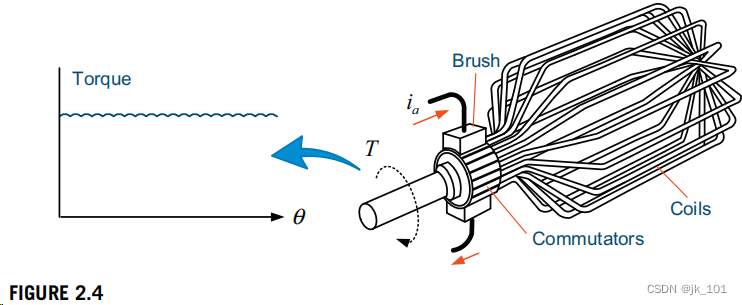
如前所述,为了使直流电机连续旋转,它的结构中必须有刷子和换向器。然而,由于电刷和换向器的磨损和电弧,直流电机需要更多的维护,并且在高速运行中受到限制。
直流电机的建模
直流电机驱动系统的完整动力学模型可以表示为以下四个公式:电枢电路、反电动势(反电动势)、转矩和机械负载系统。
电枢电路
直流电动机电枢绕组的电压方程为:

其中ia为绕组电流,La为绕组电感,Ra为绕组电阻,ea为由电枢绕组在磁场中旋转引起的反向电动势。由等式产生的直流电机的等效电路(2.1)如图2.5所示。

我们需要一个反向电动场来获得来自等式的电压Va流过电枢绕组的电流(2.1).
反电动势
如图2.6所示,当长度为l米的导体在均匀磁场B的存在下以恒定的速度v运动时,会在导体中产生一个电压e=Blv(称为反向电动势)。同样,在直流电机中,当电枢绕组的导体以角速度为ωm时在均匀定子磁通量φf存在的情况下移动时,电枢绕组中的反电动势将表示为:
![]()

其中,ke是后电场势常数(Vs/rad/Wb)。通常,由于通量保持不变,反电动势与角速度成正比。
根据施加的输入电压Va和反电场势计算出电枢电流,我们可以得到直流电机的显影转矩如下。
转矩
如图2.7所示,当长度为l米、电流为i安培的导体放置在均匀磁场B中时,作用在导体上的力将是F =Bli。类似地,在直流电机中,在均匀定子磁通量φf中携带电流ia的电枢绕组的导体所经历的转矩由

其中,kT为扭矩常数(Nm/Wb/A)。kT和ke常数的数值以SI单位(国际单位制)表示相等,即kT = ke。
值得注意的是,直流电机的转矩可以表示为定子磁通量φf和电枢电流ia的简单算术乘积。这是因为定子磁通量φf和载电流ia的导体总是相互垂直的。因此,直流电机本身具有最大扭矩特性。
转子的速度可以由发展的转矩确定如下。
机械负荷系统
当一个直流电机的输出转矩为等式时(2.3)是驱动机械载荷系统,转子转速可以由等式的运动方程确定(2.4)如第1章所述。

式中ωm为转子角速度,TL为载荷力矩,J为惯矩,B为直流电机驱动系统的摩擦系数。
由上述方程2.1)~(2.4)表示的动态模型。我们可以了解直流电机驱动系统中电流和速度的稳态和瞬态特性。首先,在此模型的基础上,我们将研究直流电机在稳态条件下的速度转矩特性。
直流电动机的稳态特性
“稳态”指的是在所有初始瞬态或波动条件都消失后存在的条件。通过对方程中变量的时间导数,在等式(2.1)和(2.4)可以很容易地确定直流电机的稳态为零,
即![]() 。从稳态方程中,速度-转矩关系可以写为:
。从稳态方程中,速度-转矩关系可以写为:

在这里,忽略了摩擦系数B。
从这个转矩-速度关系可以看出,直流电机的速度随着荷载转矩(或电枢电流)的增加而稳步减小,如图2.8所示。这里,N是角速度ωm用每分钟旋转(r/min)表示的速度。从曲线上,我们可以找到一定负载下的速度和电流。
等式(2.5)这意味着直流电机的稳态速度可以通过电枢电压Va或定子场通量φf来调节。因此,直流电机有两种速度控制方法:电枢电压控制和场磁通控制。除了这两种方法外,我们还可以从等式中看到等式(2.5)可以通过改变电枢电阻Ra来控制速度。然而,这种低效的方法已不再使用。

现在,我们将通过电枢电压控制和场通量控制来研究直流电机的速度控制特性。
电枢控制电压
当定子场通量恒定时,等式(2.5)表示扭矩-的速度特性可以降低为

其中,![]() 和
和![]()
从这个表达式可以看出,直流电机的速度ωm随电枢电压Va呈线性变化。因此,对于电梯和起重机等恒定转矩负载,可以通过调节直流电动机的电枢电压Va来线性控制负载的速度,如图2.9所示。
为了采用电枢电压控制,需要可变直流电源,如相控整流器或断流器。由于电机不应施加大于额定电压的电压,因此这种电枢电压控制方法只能提供高达额定速度的速度控制范围。为了在高于额定速度的速度范围内运行,直流电机必须采用现场磁通控制,这将在后面描述。然而,永磁直流电机不能使用现场磁通量控制方法,因此它们不能在额定速度以上运行。

磁场通量控制
在一个恒定的电枢电压下,等式(2.5)可以重写为场通量的函数:

其中,![]()
根据等式(2.7),我们可以看到直流电机的速度随场通量成反比。图2.10显示了使用磁场通量控制的直流电机的转矩速度特性。当使用该场磁通控制方法时,场磁通必须控制在额定值以下,以避免铁芯的磁饱和,因为额定磁通通常是磁化曲线膝盖附近的值,如图2.10左侧所示。如果磁场通量低于额定值,则速度可以增加高于额定速度。
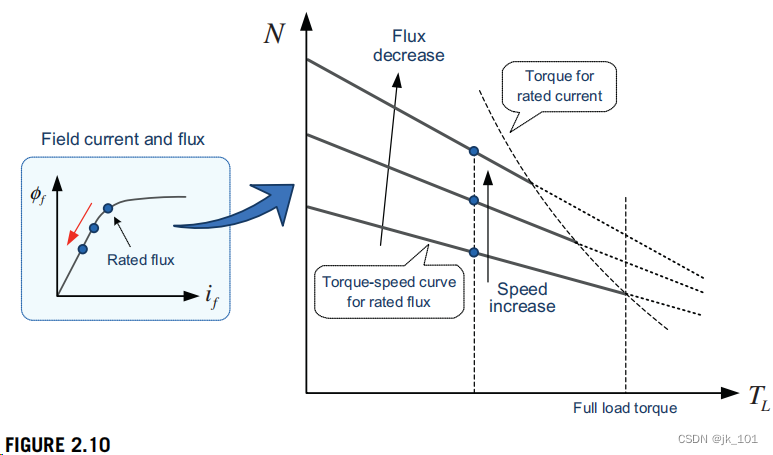
当通过调整现场通量控制,可以将直流电机的速度控制在额定值以上时,就会出现潜在的问题。当降低场通量以增加速度时,相同电枢电流的发展转矩也会减小。如果增加电枢电流以产生相同的扭矩,则由于铜损耗的增加,效率将会降低。由于热限制和直流电源的容量,电枢电流也可能不会完全增加。此外,场绕组的电感通常设计为较大,以有效地产生通量。因此,场通量不能迅速改变,这将导致速度调节的响应缓慢。此外,在高速范围内,速度调节将较差的施加负荷,并产生较低的场通量很容易受到电枢反应的影响。除了这些电气问题外,直流电动机还受到机械换向装置的速度限制。因此,这种场通量控制的可实现的速度范围通常被限制在额定速度的三倍以内。
直流电机的运行区域
直流电机的工作速度范围分为以下两个区域:恒转矩区域和恒功率区域。这两个区域的工作可以通过电枢电压控制和场通量控制来实现。
恒定扭矩区域(0 <=ωm <=基本速度<=ωb)
在低于额定速度的工作区域内,场磁通量保持在一个恒定的水平,而转矩的产生仅由电枢电流Ia控制。这个区域被称为恒定转矩区域,因为在这个区域内的任何速度下,相同的电枢电流都可以产生相同的转矩。
随着工作速度的提高,后电场力也增加。因此,还应增加所施加的电机电压,以保持相同的电枢电流,即相同的转矩。就这样,在这个区域内,直流电动机的终端电压随其速度而变化。由于施加到电机上的电压不应超过额定值,因此该区域的范围通常被限制为直流电机的终端电压达到额定值时的速度。根据操作条件,此转速可能与额定转速不同。因此,它通常被称为基本速度ωb。
恒定功率区域(ωm >=基本速度):场减弱区域
一旦电机电压达到额定值,速度就不能再由电压控制了。当速度高于基本速度时,所施加的电压保持不变。因此,可以代替电压控制,而通过减少场通量来提高速度(称为场弱化操作)。无论速度增加,场通量的减少都能使反电场恒定。这使得产生转矩的电枢电流得以流动。然而,即使有相同的电流流动,由于场通量的减少,输出转矩也会随着工作速度的降低而降低。由于该区域的终端电压和电流保持恒定,电机工作在恒定功率,![]() 。因此,这个速度区域被称为恒定功率区域。
。因此,这个速度区域被称为恒定功率区域。
图2.11显示了直流电动机的速度转矩特性,通常称为能力曲线。性能曲线显示了电机在可用电压和电流条件下的可达速度范围和输出转矩。对于具有第1.3.2节中所述的四象限操作模式的直流电机驱动器,这种速度转矩特性出现在所有四个象限中。考虑到电枢电阻和损耗的电压降,象限2和4的输出转矩略大于象限1和象限3的输出转矩:

对于四象限操作,需要反转输出扭矩的方向,以改变转子的旋转方向。在这种情况下,改变电枢电流的极性将会更有效。即使可以通过反转场通量的极性来改变转矩的方向,但由于场绕组的电感较大,其响应速度较慢,因此驱动系统的稳定性可能会恶化。
示例1
单独励磁直流电动机的额定值为5 kW、140 V、1800 r/min,效率η为91%(忽略机械损失和铁损失等损失)。电枢阻力为0.25 Ω。评估以下问题。
1. 电枢电流和额定转矩
2. 当电枢电压降低10%时的满载速度
3. 当通量减少10%时,在满载电流下的速度和在该速度下通过电枢电流可用的输出转矩
解决
1.从输入功率和输出功率的关系可知,输入输出功率为

电枢电流为
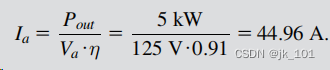
从输出功率输出![]() ,额定扭矩为:
,额定扭矩为:

2.电枢电压降低10%,Vnew,为112.5V。在这个电压下,速度为

其中,![]()
3.在通量下降低10%的速度是

在这个速度下,电枢电流可用的输出扭矩为
![]()
直流电机的瞬态响应特性
在第2.3节中,我们研究了直流电机的稳态特性,这证明了通过电枢电压或场通量的速度控制。稳态特性显示了最终速度是什么,而瞬态响应显示了如何达到最终速度。除了稳态特性外,瞬态特性对高性能电机驱动也非常重要。这是因为瞬态响应描述了驱动系统的动力学特性。例如,对步进速度命令的瞬态响应如图2.12所示。

尽管这三种反应都达到了相同的最终速度,但它们的响应时间和达到最终速度的移动轨迹都是不同的。虽然一个振荡或缓慢的响应最终可以实现速度命令,但它没有实际用途。因此,我们需要考虑到高性能电机驱动器的瞬态特性和稳态特性。
现在,让我们来看看直流电动机通过施加的电枢电压达到最终速度时的瞬态响应。检验瞬态响应的一个简单方法是利用系统的传递函数。我们可以得到采用等式(2.1)和(2.4)微分方程的拉普拉斯变换得到直流电机驱动系统的传递函数如下。

这里,s表示拉普拉斯算符。“公式”。(2.8)和(2.9)一起放在一起,可以用如图2.13所示的闭环方框图来表示。

根据图2.13中的方框图,从输入电枢电压VaðsÞ到输出角速度ωmðsÞ的传递函数为

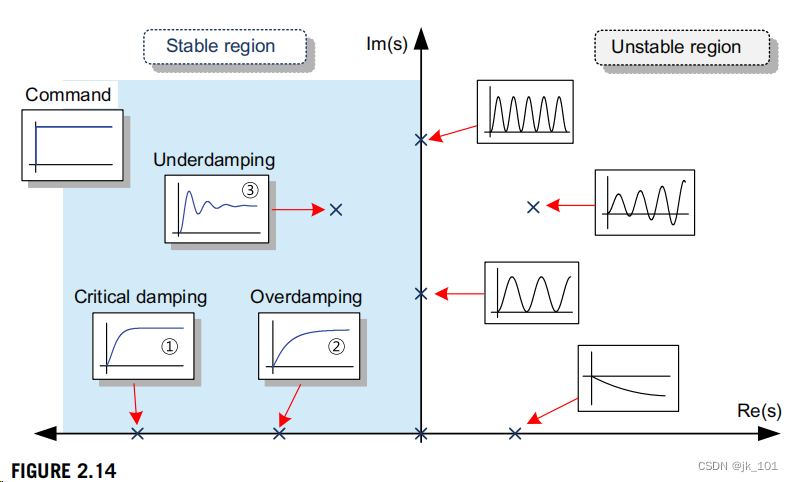
该传递函数是一个包含两个极点的二阶系统,它是决定系统瞬态响应的重要因素。图2.14显示了一个系统在s平面上的极点位置和相应的瞬态响应。极点的虚轴位置决定了响应中振荡的频率。因此,如果极点是复根,则响应是振荡的。极点的实轴位置决定了瞬态情况的指数衰减速度。因此,在s平面上,极点距离原点越远,瞬态情况消失得就越快,即系统达到最终值的速度就越快。
闭环传递函数
具有反馈回路的系统具有以下传递函数:

根据等式(2.10)的两极的位置,我们可以预测速度对所施加的电枢电压的瞬态响应。因此,瞬态响应在很大程度上取决于系统参数,如电机参数Ra和La,以及机械参数J和B,如下图所示。
假设等式(2.10)中的B= 0为了便于分析该系统,我们可以得到一个简化的传递函数为:

让机电时间常数![]() 和电时间常数
和电时间常数![]() ,等式(2.11)可以重写为
,等式(2.11)可以重写为
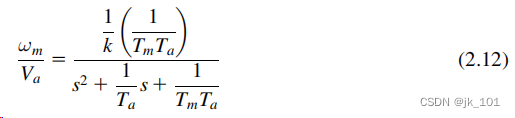
这些极点可以从等式的分母(也称为特征方程)的根中得到等式(2.12)为

如果Tm>=4Ta,则特征方程有两个实根。一个具有较大的J或Ra的直流电机驱动系统对应于此情况,其响应在图2.14中为➀或➁。如果Tm<=4Ta,则特征方程有两个复根。在这种情况下,系统的响应是振荡的,如图2.14中的➂。
我们还可以从阻尼比中这个二阶系统的响应特性。为此,我们将这个方程与下面的二阶系统的原型进行了比较。

给定的等式(2.14),直流电机驱动系统的无阻尼固有频率ωn和阻尼比ζ分别为

根据阻尼比ζ的值,系统有三种典型响应:欠阻尼(0<ζ<1)、临界阻尼(ζ =1)或过阻尼(ζ>1)[1]。如图2.15所示,在阻尼不足(0<ζ<1)的情况下,系统迅速达到平衡,但有轻微的振荡响应。随着ζ值的增加,振荡量逐渐减少。在过阻尼(ζ>1)的情况下,系统不是振荡的,但响应非常慢。一个极限阻尼系统响应(ζ=1)是最理想的,它能尽快达到平衡,而不是振荡。

平衡(2.16)意味着阻尼比ζ,即速度对施加的电枢电压的动态性能,取决于机电时间常数值Tm和电时间常数值Ta。如果Tm<4Ta,则ζ<1及其速度响应将为振荡。相比之下,在Tm>=4Ta的情况下,系统将具有稳定的速度响应,无振荡。
通常,小型电机带有Tm>4Ta,而伺服电机或高功率电机有T<4Ta,从而产生振荡响应。即使系统响应本质上是振荡的,我们也可以通过采用一个适当的控制器来实现期望的响应,这将在后面描述。
在大多数电机驱动系统中,电力系统的时间响应比机械系统的时间响应要快。在这种情况下,我们可以忽略电路的瞬态,使La=0。因此,等式(2.11)可以写成
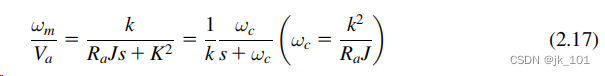
该方程表明,在直流电机中,速度ωm与电枢电压Va之间的关系可以看作是具有截止频率ωc的一阶低通滤波器。这意味着速度ωm与电枢电压Va成正比,其变化速率低于ωc,尽管两者之间有一个时间延迟。一般可以假定直流电机的转速与施加给它的电压成正比。

![[网鼎杯 2020 青龙组]singal 1](https://img-blog.csdnimg.cn/direct/7235c021c4cf45edaccf557910d797f7.png)