根据序列恢复二叉树

示例

给定序列恢复二叉树
(1)前序：1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
(2)中序：3 4 8 6 7 5 2 1 10 9 11 15 13 14 12
3)后序：8 7 6 5 4 3 2 10 15 14 13 12 11 9 1

一、前中序列恢复二叉树

(1)前序：1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
(2)中序：3 4 8 6 7 5 2 1 10 9 11 15 13 14 12
我们知道前序第一个访问的就是根节点，所以根节点就是1。
中序遍历的特点是根节点的左子树的元素都在根节点的左侧，右子树的元素都在根节点的右侧，从中序遍历序列我们可以划分成如下结构：

此时由中序序列可知
根结点：1
左子树：3 4 8 6 7 5 2
右子树：10 9 11 15 13 14 12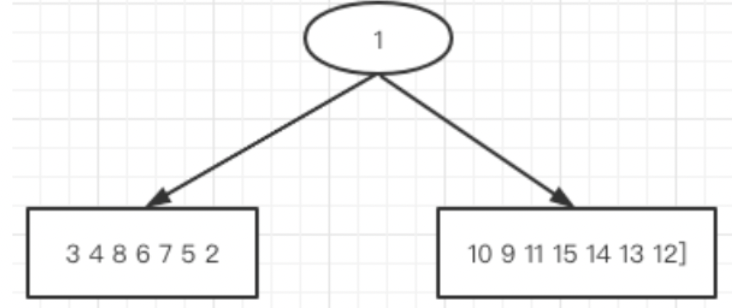

然后对划分出的两个子树按照前面的步骤继续划分
如左子树
前序序列：2 3 4 5 6 8 7
中序序列：3 4 8 6 7 5 2
根据前序的根结点2对中序序列进行划分

由中序序列可知
根结点：2
左子树： 3 4 8 6 7 5
右子树：空

最终经过多轮划分，最终二叉树的结构如下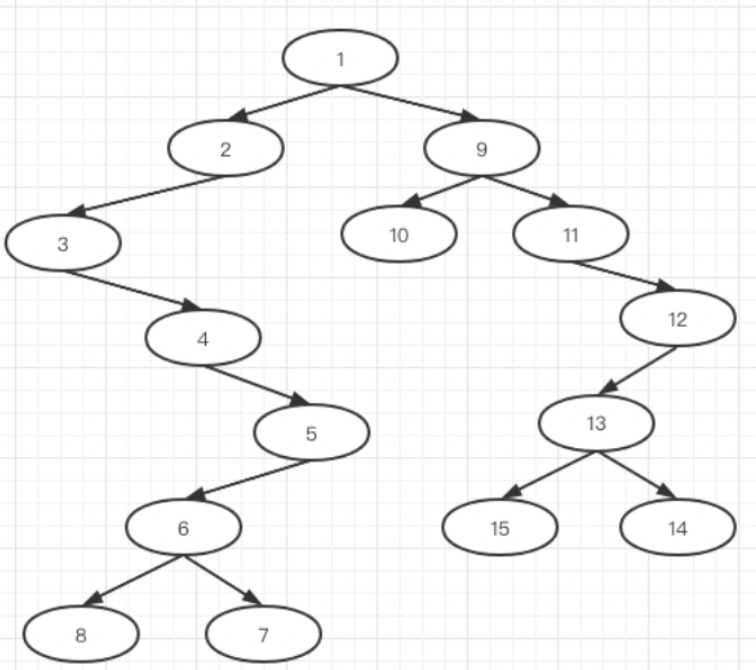

二、中后序列恢复二叉树

(2)中序：3 4 8 6 7 5 2 1 10 9 11 15 13 14 12
3)后序：8 7 6 5 4 3 2 10 15 14 13 12 11 9 1
与前中序列恢复二叉树类似，只是此时根结点在后序序列的末尾，即1。然后根据1对中序序列进行划分，可得

中序：[3 4 8 6 7 5 2] 1 [10 9 11 15 13 14 12]
后序：[8 7 6 5 4 3 2] [10 15 14 13 12 11 9] 1

有中序的划分可知
根结点：1
左子树：3 4 8 6 7 5 2
右子树：10 9 11 15 13 14 12

三、注意

既然上面两种都行，那为什么前序和后序不行呢？看上面的例子：
(1)前序：1 2 3 4 5 6 8 7 9 10 11 12 13 15 14
(2)后序：8 7 6 5 4 3 2 10 15 14 13 12 11 9 1
根据上面的说明，我们通过前序可以知道根节点是1，通过后序也能知道根节点是1，但是中间是怎么划分的呢？其他元素哪些属于左子树，哪些属于右子树呢？很明显通过两个序列都不知道，所以前序和后序序列不能恢复二叉树。