题目1：139 单词拆分

题目链接：单词拆分

对题目的理解

字符串列表wordDict作为字典，判断是否可以利用字典中出现的单词拼接出字符串s，字典中的单词可以重复使用，题目中字符串s的长度至少为1，不存在空字符的现象

字典中的单词可以重复使用，说明是一个完全背包问题

字典wordDict中的单词就是物品，字符串s就是背包，将字符串进行划分，单词能不能填满字符串

动规五部曲

1）dp数组及下标i的含义

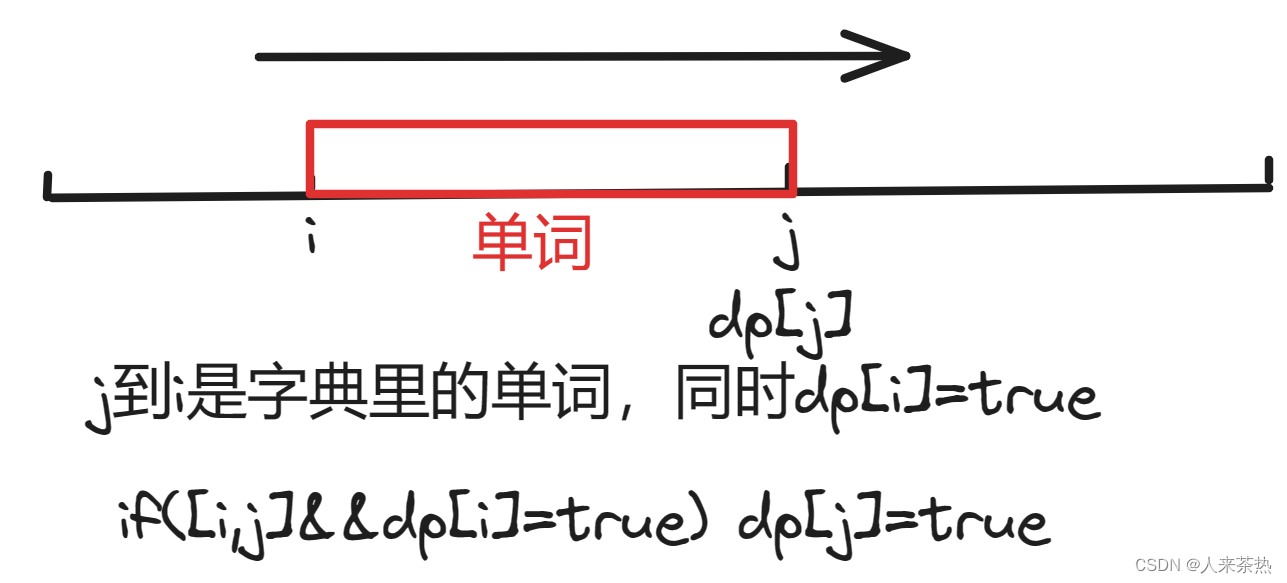
dp[j]:字符串的长度是j时，能否被字典中的单词组成（dp[j]=true   or     dp[j]=false)

最终判断dp[s.size()]

2）递推公式

3）dp数组初始化

dp[0]表示空字符串,字符串长度为0，题目要求字符串s的长度至少为1，所以出现空字符串没有意义，dp[0]设置为true，递推公式dp[j]的状态依赖于前面dp[i]，只是为了递推公式，是基础，如果是false的话，根据递推公式1往后推，后面的都为false，

其他非零下标dp[j]设置为false，以免覆盖后面递推得到的关系

4）遍历顺序

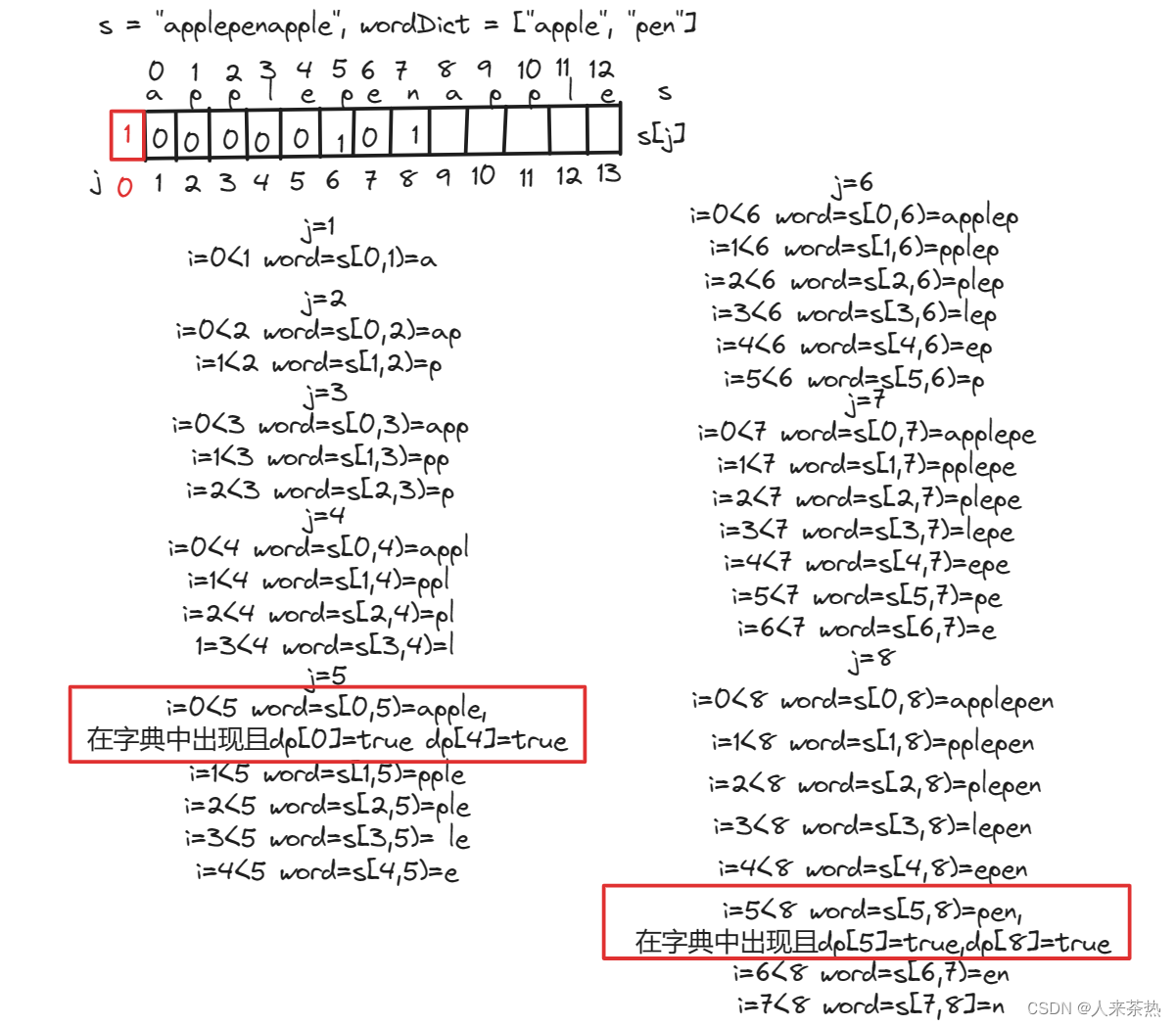
拿 s = "applepenapple", wordDict = ["apple", "pen"] 举例。

"apple", "pen" 是物品，只有物品的组合一定是 "apple" + "pen" + "apple" 才能组成 "applepenapple"。

"apple" + "apple" + "pen" 或者 "pen" + "apple" + "apple" 是不可以的，那么强调物品之间顺序，因为字符串中每个单词的状态取决于前一个单词的状态，比如，pen取决于apple是否在字典中，如果apple在字典中，返回true，那么后面的pen在字典中找到，也返回true，如果apple未在字典中找到，即使后面的pen在字典中找到，那么pen对应的也返回false。所以，如果先遍历物品（单词）的话，即使每一个物品（单词）可以使用多次，那么由于中间夹着的其他单词还未在字典中一一对应，那么相同的单词（由数个其他单词分隔）中，后面的单词（第2个apple）也不会返回true。

所以说，本题一定是 先遍历 背包，再遍历物品（排列）。

substr的含义是substr(begin,interval)begin代表区间的起始，interval代表整个区间的长度，注意是长度，不是结尾

5）打印dp数组

代码流程及代码

代码流程(先遍历背包后遍历物品)

代码

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> wordset(wordDict.begin(),wordDict.end());
        //定义并初始化dp数组
        vector<bool> dp(s.size()+1,false);
        dp[0]=true;
        //递推，先正序遍历背包，后正序遍历物品
        for(int j=1;j<=s.size();j++){//背包,字符串s
            for(int i=0;i<j;i++){
                string word = s.substr(i,j-i);//截取i到j之间的单词
                if(wordset.find(word)!=wordset.end() && dp[i]==true) dp[j]=true;
            }
        }
        return dp[s.size()];
    }
};

• 时间复杂度：O(n^3)，因为substr返回子串的副本是O(n)的复杂度（这里的n是substring的长度）
• 空间复杂度：O(n)

代码流程（非背包问题考虑）

不把本题考虑成背包问题的话，直接遍历字符串也是可以的，使用两个for循环，流程如下

代码

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> wordset(wordDict.begin(),wordDict.end());
        //定义并初始化dp数组
        vector<bool> dp(s.size()+1,false);
        dp[0]=true;
        //递推
        for(int i=0;i<s.size();i++){
            for(int j=i+1;j<=s.size();j++){
                string word = s.substr(i,j-i);//截取i到j之间的单词
                cout<<"j="<<j<<endl;
                cout<<"i="<<i<<endl;
                cout<<word<<endl;
                if(wordset.find(word)!=wordset.end() && dp[i]==true) dp[j]=true; 
                cout<<"dp[j=]"<<dp[j]<<endl;
            }
        }
        return dp[s.size()];
    }
};

代码流程（先遍历物品后遍历背包）这个代码放入测试用例会报错

如果是先遍历物品，再遍历背包（组合）的话，因为前面的pen还没有遍历到，所以不会被赋值成true，所以就会导致最后的一个apple不会被赋值为true

代码

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> wordset(wordDict.begin(),wordDict.end());
        //定义并初始化dp数组
        vector<bool> dp(s.size()+1,false);
        dp[0]=true;
        //递推
        for(int i=0;i<wordDict.size();i++){//物品,字符串s
            for(int j=wordDict[i].size();j<=s.size();j++){//背包
                string word = s.substr(j-wordDict[i].size(),wordDict[i].size());//截取i到j之间的单词
                if(word==wordDict[i] && dp[j-wordDict[i].size()]==true) dp[j]=true; 
            }
        }
        return dp[s.size()];
    }
};

题目2：多重背包

题目链接：多重背包

对题目的理解

N种物品，容量为V的背包，第i种物品最多有Mi件可用，每件耗费的空间是Ci，价值是Wi

求解，将哪些物品装入背包可使这些物品耗费的空间总和不超过背包容量，且价值总和最大

每件物品最多有Mi件可用，把Mi件摊开，其实就是一个01背包问题了

代码

#include<iostream>
#include<vector>
using namespace std;
int main(){
    int C,N;//C是容量，N是矿石的种类
    cin>>C>>N;
    vector<int> weight(N,0);
    for(int i=0;i<N;i++){
        cin>>weight[i];
    }
    vector<int> value(N,0);
    for(int i=0;i<N;i++){
        cin>>value[i];
    }
    vector<int> nums(N,0);
    for(int i=0;i<N;i++){
        cin>>nums[i];
    }
    for(int i=0;i<N;i++){
        while(nums[i]>1){//这里大于1的原因是因为前面已经放置了这种石头，所以只需要再放多余1的石头即可
            weight.push_back(weight[i]);
            value.push_back(value[i]);
            nums[i]--;
        }
    }//转化为1个01背包问题
    //定义并初始化dp数组
    vector<int> dp(C+1,0);
    //递推,先正序遍历物品，后倒序遍历背包
    for(int i=0;i<weight.size();i++){
        for(int j=C;j>=weight[i];j--){
            dp[j]=max(dp[j],dp[j-weight[i]]+value[i]);
        }
    }
    cout<<dp[C]<<endl;
}

这段代码会超时，如果物品数量很多的话，C++中，这种操作十分费时，主要消耗在vector的动态底层扩容上。（其实这里也可以优化，先把 所有物品数量都计算好，一起申请vector的空间。

也有另一种实现方式，就是把每种商品遍历的个数放在01背包里面在遍历一遍。

代码

#include<iostream>
#include<vector>
using namespace std;
int main(){
    int C,N;//C是容量，N是矿石的种类
    cin>>C>>N;
    vector<int> weight(N,0);
    for(int i=0;i<N;i++){
        cin>>weight[i];
    }
    vector<int> value(N,0);
    for(int i=0;i<N;i++){
        cin>>value[i];
    }
    vector<int> nums(N,0);
    for(int i=0;i<N;i++){
        cin>>nums[i];
    }
    //定义并初始化dp数组
    vector<int> dp(C+1,0);
    //递推,先正序遍历物品，后倒序遍历背包
    for(int i=0;i<N;i++){//物品种类
        for(int j=C;j>=weight[i];j--){
            for(int k=1;k<=nums[i] && (j-k*weight[i])>=0;k++)//相同种类遍历个数
            dp[j]=max(dp[j],dp[j-k*weight[i]]+k*value[i]);
        }
    }
    cout<<dp[C]<<endl;

    
    
}

时间复杂度：O(m × n × k)，m物品种类个数，n背包容量，k单类物品数量

从代码里可以看出是01背包里面再加一个for循环遍历一个每种商品的数量，和01背包还是如出一辙的。

多重背包在面试中基本不会出现，对多重背包的掌握程度知道它是一种01背包，并能在01背包的基础上写出对应代码就可以了。