代码模块参考文章:传教士与野人过河问题(numpy、pandas)_python过河问题_醉蕤的博客-CSDN博客
问题描述
一般的传教士和野人问题(Missionaries and Cannibals):有N个传教士和C个野人来到河边准 备渡河。河岸有一条船,每次至多可供K人乘渡。 问传教士为了安全起见,应如何规划摆渡方案,使 得任何时刻,在河的两岸以及船上的野人数目总是 不超过传教士的数目,但允许在河的某一岸只有野 人而没有传教士。
这里讨论基于N=3,C=3,k=2
状态表示:(m,w,B);初始状态: (3, 3, 1);目标状态: (0,0,0)
启发性规则
操作符(产生式规则)
左岸往右岸运载产生式
L10 if(M,W,1) then (M-1,W,0) (左往右运1传教士)
L01 if(M,W,1) then (M,W-1,0) (左往右运1野人)
L11 if(M,W,1) then (M-1,W-1,0) (左往右运1传教士和1野人)
L20 if(M,W,1) then (M-2,W,0) (左往右运2传教士)
L02 if(M,W,1) then (M,W-2,0) (左往右运2野人)
右岸往左岸运载产生式
R10 if(M,W,0) then (M+1,W,1) (右往左运1传教士)
R01 if(M,W,0) then (M,W+1,1) (右往左运1野人)
R11 if(M,W,0) then (M+1,W+1,1) (右往左运1传教士和1野人)
R20 if(M,W,0) then (M+2,W,1) (右往左运2传教士)
R02 if(M,W,0) then (M,W+2,1) (右往左运2野人)
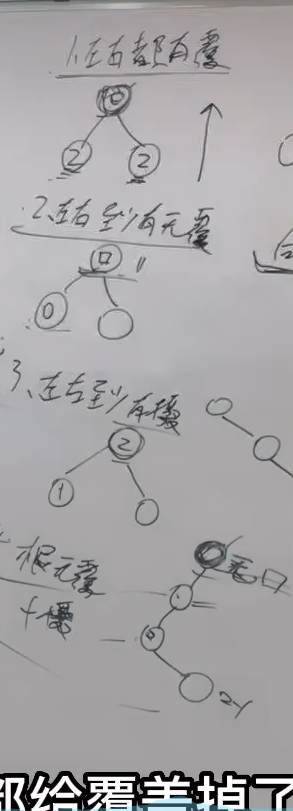
路径方案展示
总共有四种解决方案
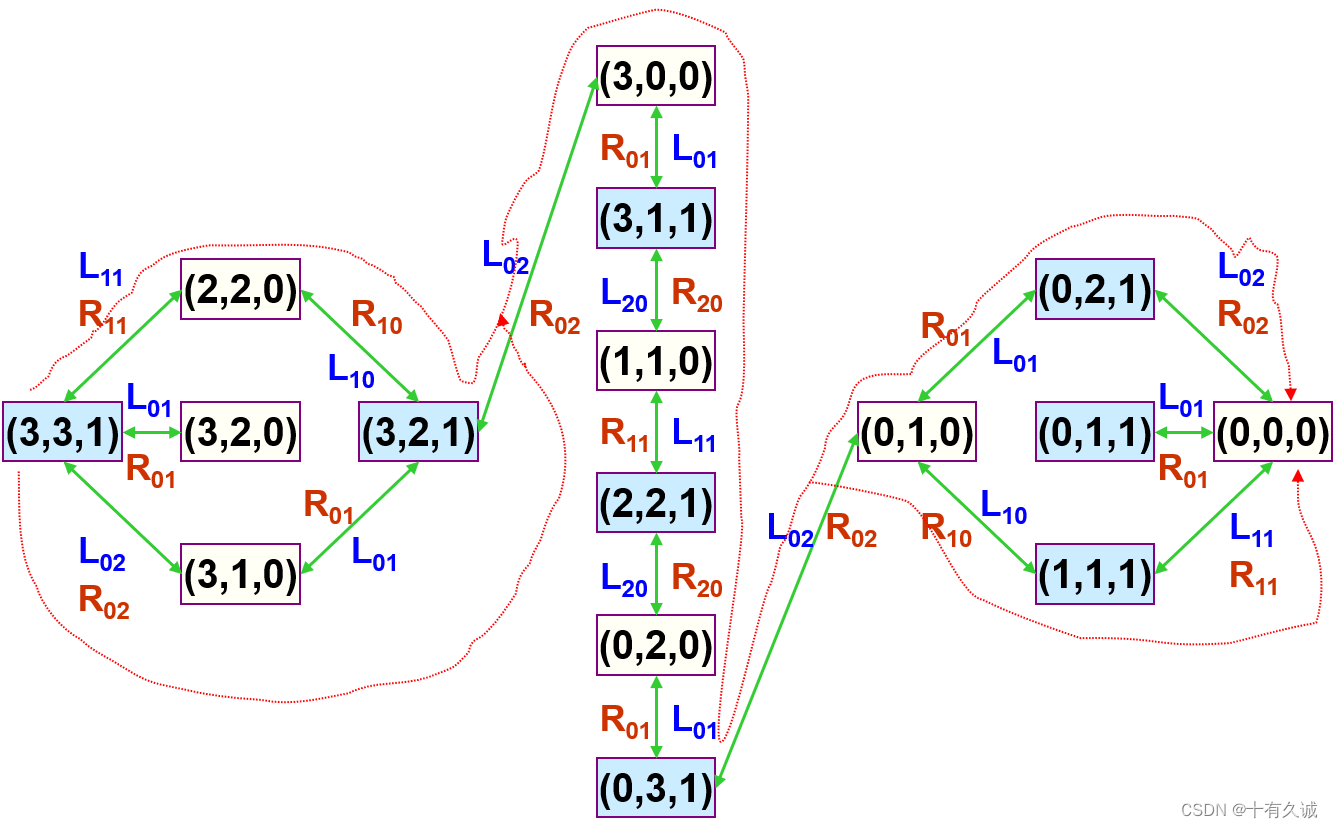
实现代码(含具体解释)
import numpy as np
M = int(input("请输入传教士的数量:")) # 传教士数量
C = int(input("请输入野人的数量:")) # 野人数量
K = int(input("请输入船的最大容量:")) # 船的最大容量
child = [] # child:用于存储所有扩展节点
open_list = [] # open list
closed_list = [] # closed list
class State:
def __init__(self, m, c, b):
self.m = m # 左岸传教士的数量
self.c = c # 左岸野人的数量
self.b = b # b为1时船在左岸;b为0时船在右岸
self.g = 0 # 该结点所在的层级
self.f = 0 # 该结点的启发性层度f = g + h
# father这个属性是State
self.father = None
self.node = np.array([m, c, b])
init = State(M, C, 1) # 初始节点
goal = State(0, 0, 0) # 目标节点
# 判断状态是否合法
def safe(s):
# 下面是要排除的条件,并且给出了为什么要排除的理由
# s.m > M or s.m < 0 题目要求传教士的数量
# s.c < 0 or (s.m != 0 and s.m < s.c) 有教士时,野兽的数量不能大于教士
# s.m != M and M - s.m < C - s.c 对岸不全是怪兽时,对岸上的怪兽不能大于对岸上的教士
if s.m > M or s.m < 0 or s.c > C or s.c < 0 or (s.m != 0 and s.m < s.c) or (s.m != M and M - s.m < C - s.c):
return False
else:
# 状态合法
return True
# 启发函数
def h(s):
# 传教士数量+野人数量-船的位置与船的最大容量的乘积
# 我们希望这个值越越小越好
# 他的含义:岸上传教士数量+岸上野人数量之后
# 如果这船在对岸(这是我们希望的,说明顺利渡河),于是我们就减上K*s.b
# 如果船不在对岸,这不是我们希望的,所以不进行任何减数的操作(K=0)
return s.m + s.c - K * s.b
# 判断两个状态是否相同
def equal(a, b):
if np.array_equal(a.node, b.node):
return 1, b
else:
return 0, b
# 判断当前状态是否与父状态一致
# new 是新结点,s是它的父节点
def back(new, s):
if s.father is None:
return False
c = b = s.father
while True:
# 不断回溯,去找他的父结点是否与new结点相同
a, c = equal(new, b)
if a:
return True
b = c.father
if b is None:
# 此时找到的b是根结点,停止搜索
return False
# 根据f值对open_list进行排序
def open_sort(l):
l.sort(key=lambda x: x.f)
# 在open_list和closed_list中查找具有相同MCB属性的节点
def in_list(new, l):
for item in l:
if np.array_equal(new.node, item.node):
return True, item
return False, None
# A*算法
def A_star(s):
A = []
global open_list, closed_list
open_list = [s]
closed_list = []
while True: # open_list不为空
for i in open_list:
if np.array_equal(i.node, goal.node): # 判断是否为目标节点
A.append(i)
open_list.remove(i)
if not open_list:
break
get = open_list[0]
open_list.remove(get) # 从open_list中移除get节点
closed_list.append(get) # 将get节点加入closed_list
# 获取get的子节点并考虑是否将其加入open_list
for i in range(M + 1): # 船上传教士数量
for j in range(C + 1): # 船上野人数量
# 船上人数非法: 1:船上无人或者2:船上的人大于规定的载客数或者3:船上有教士并且野怪的数量大于教士
if i + j == 0 or i + j > K or (i != 0 and i < j):
continue
# 找到满足要求的相对于刚遍历完的结点get的下一个状态
if get.b == 1: # 当前船在左岸,下一个状态船在右岸
new = State(get.m - i, get.c - j, 0)
child.append(new)
else: # 当前船在右岸,下一个状态船在左岸
new = State(get.m + i, get.c + j, 1)
child.append(new)
# safe(new)判断是否非法
# back(new, get)这个相对于get结点的孩子回到父状态? TODO
if not safe(new) or back(new, get): # 状态非法或已经回到父状态
child.pop()
else:
# 定义它的上一个状态的结点
new.father = get
# 孩子结点层级加1
new.g = get.g + 1
# 父亲的结点层级+父亲的启发性层度
new.f = get.g + h(get)
open_list.append(new)
open_sort(open_list)
return A
# 递归打印路径
def print_path(f):
if f is None:
return
# 先递归打印父结点的,再打印自己的结点
print_path(f.father)
print(f.node)
# print(f.f)
if __name__ == '__main__':
print('传教士数量:%d, 野人数量:%d, 船的最大容量:%d' % (M, C, K))
final = A_star(init)
print("共有%d种方案" % len(final))
if final:
c = 1
for i in final:
print('第%d个方案如下' % c)
print_path(i)
c += 1
else:
print('没有找到解决方案!')