矩阵代数的相关知识

目录

一、特征值与特征向量

1、特征值与特征向量

2、MATLAB计算

二、广义特征值与广义特征向量

1、广义特征值与广义特征向量

2、MATLAB计算

三、酋矩阵

1、酋矩阵

2、MATLAB计算

四、未完待续

总结

---

提示：以下是本篇文章正文内容，写文章实属不易，希望能帮助到各位，转载请附上链接。

一、特征值与特征向量

1、特征值与特征向量

令,若标量和非零向量满足方程

则称是矩阵的特征值，是与对应的特征向量。特征值可能为零，但特征向量一定非零。特征值与特征向量总是成对出现，称为矩阵的特征对。

2、MATLAB计算

%% 特征值与特征向量
A=[1 2 4;0 2 0;2 -1 3];
[V,D]=eig(A) %V的每一列是特征向量，D的对角元素是特征值
A*V(:,1)
-1*V(:,1)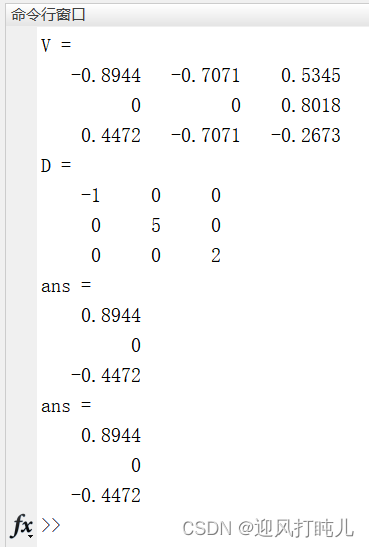

二、广义特征值与广义特征向量

1、广义特征值与广义特征向量

令,若标量和非零向量满足方程

则称是矩阵相对于矩阵的广义特征值，是与对应的广义特征向量。特别的，当矩阵为单位阵时，就成了普通的特征值问题。

2、MATLAB计算

%% 广义特征值与广义特征向量
A=[1 2 4;0 2 0;2 -1 3];
B=[2 -1 1;0 3 -1;2 1 3];
[V,D]=eig(A,B) %V的每一列是广义特征向量，D的对角元素是广义特征值
A*V(:,1)
-1.3011*B*V(:,1)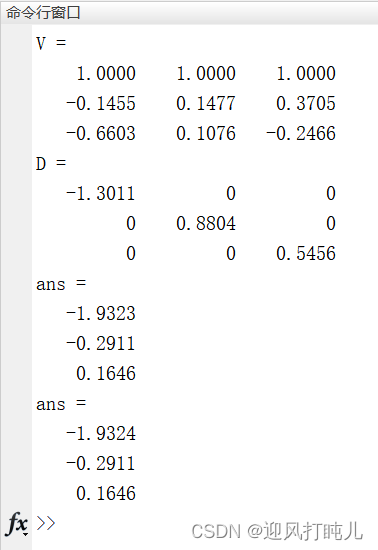

三、酋矩阵

1、酋矩阵

若,如果，其中'H'表示共轭转置，表示单位矩阵，则称矩阵为酋矩阵。  对于酋矩阵，。

2、MATLAB计算

%% 酋矩阵验证
A=[(-1-1i)/2 (-1-1i)/2;(1+1i)/2 (-1-1i)/2]
inv_A=inv(A)
A*A'

四、未完待续

---

总结

以上就是要讲的内容，本文介绍了矩阵代数的相关知识及其MATLAB的计算，希望对大家有所帮助。