Problem: 347. 前 K 个高频元素

前言

对于求取Top K一般有如下两种题型：

1.针对静态数据（查询TopK操作）
2.针对动态数据（包括添加数据操作和查询TOPK操作）

一般解决思路有如下三种：

1.排序，然后取数组中的第k个元素（一般针对静态数据）
2.利用快速排序算法的思想，做到$O(n)$（一般针对静态数据）
3.利用堆，插入$O(logk)$,获取$O(1)$（一般针对动态数据）

题目描述

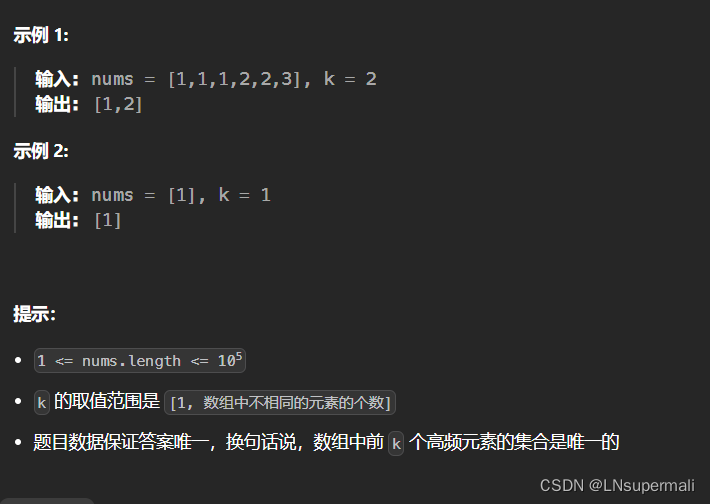
给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

思路

思路1：堆

1.维护一个大小为K的小顶堆，当有数据被添加到集合中时，
2.如果堆中的数据个数小于k，我们将新的数据直接插入到小顶堆，
3.如果堆中的数据等于K，我们就拿新添加的数据与堆顶元素比较

3.1. 如果新添加的数据大于堆顶元素，我们就把堆顶元素删除，并且这个新添加的数据插入到堆中；
3.2. 如果新添加的数据小于等于堆顶元素，则不对堆做处理。

即小堆顶中一直都是维护当前数据集合中的Top K,每次询问当前数据的Top K操作就变得比较高效，直接输出小顶堆中的元素即可。

思路2：快速排序

我们先统计出每个元素出现的频率，再以出现频率为基准进行快排

解题方法

解法1：堆

1.创建内部类，便于后面在构建小顶堆时记录每个元素出现与其出现的次数
2.利用HashMap统计每个元素与其出现的次数
3.利用思路中的步骤3维护小顶堆
4.取出k次当前小顶堆的堆顶元素到结果数组中

解法2：快速排序

1.先利用HashMap统计每个元素与其出现的次数
2.将频率字典处理为 List，以便按频率排序
3.编写并执行快速排序，按频率的从高到低排序
4.将前k高频率的元素添加到结果数组并返回

复杂度

堆：
时间复杂度:

$O(nlogk)$

空间复杂度:

$O(n)$

快速排序：
时间复杂度:

$O(nlogn)$

空间复杂度:

$O(n)$

Code

最小堆代码：

class Solution {
    private class QElement {
        int val;
        int count;

        public QElement(int val, int count) {
            this.val = val;
            this.count = count;
        }
    }

    /**
     * 利用最小堆维护前K大元素
     *
     * @param nums 待查询的数组
     * @param k    整数k
     * @return     int[]
     */
    public int[] topKFrequent(int[] nums, int k) {
        //哈希表统计每个数字出现的count
        Map<Integer, Integer> counts = new HashMap<>();
        for (int num : nums) {
            counts.put(num, counts.getOrDefault(num, 0) + 1);
        }
        //按照count构建小顶堆
        PriorityQueue<QElement> minQueue = new PriorityQueue<>(new Comparator<QElement>() {
            @Override
            public int compare(QElement o1, QElement o2) {
                return o1.count - o2.count;
            }
        });
        //求取top k
        for (Map.Entry<Integer, Integer> entry : counts.entrySet()) {
            int key = entry.getKey();
            int count = entry.getValue();
            //如果堆中元素的个数小于k，直接加入
            if (minQueue.size() < k) {
                minQueue.offer(new QElement(key, count));
            } else {
                //如果堆顶元素小于当前数字的频率
                //则删除原来堆顶元素，重新加入
                //当前的数字的频率
                if (minQueue.peek().count < count) {
                    minQueue.poll();
                    minQueue.offer(new QElement(key, count));
                }
            }
        }
        int[] result = new int[k];
        for (int i = 0; i < k; ++i) {
            result[i] = minQueue.poll().val;
        }
        return result;
    }
}

快速排序代码：

class Solution {
    /**
     * 求取数组中的频率前K大函数
     *
     * @param nums 待求取数组
     * @param k    给定的数字
     * @return int[]
     */
    public int[] topKFrequent(int[] nums, int k) {
        if (nums.length == 1) {
            return new int[]{nums[0]};
        }
        /* 以下计算频率 */
        Map<Integer, Integer> frequentMap = new HashMap<>();
        for (int num : nums) {
            frequentMap.put(num, frequentMap.getOrDefault(num, 0) + 1);
        }
        int n = frequentMap.size();

        /* 以下将频率字典处理为 List，以便按频率排序(这里元素类型选择 int[] 而不是 Entry，可以避免后续排序阶段拆箱) */
        List<int[]> frequentList = new ArrayList<>(n);
        for (Map.Entry<Integer, Integer> entry : frequentMap.entrySet()) {
            frequentList.add(new int[]{entry.getKey(), entry.getValue()});
        }

        /* 执行快速排序(选择), 注意这里讲频率高的排在前面 */
        quickSort(frequentList, 0, n - 1);

        /* 将频率列表中最右边 K 个元素返回即可 */
        int[] ans = new int[k];
        for (int i = 0; i < k; i++) {
            ans[i] = frequentList.get(i)[0];
        }
        return ans;
    }

    /**
     * 快速排序函数
     *
     * @param list  待排序的数组
     * @param left  待排序数组的左端点
     * @param right 待排序数组的右端点
     */
    public void quickSort(List<int[]> list, int left, int right) {
        if (left >= right) {
            return;
        }
        int q = partition(list, left, right);
        quickSort(list, left, q - 1);
        quickSort(list, q + 1, right);
    }

    /**
     * 找出数组分区点
     *
     * @param nums  待分区数组
     * @param left  待分区数组的左端点
     * @param right 待分区数组的右端点
     * @return int
     */
    public int partition(List<int[]> nums, int left, int right) {
        /* CLRS 中的写法 */
        int[] pivot = nums.get(right);
        int i = left - 1;
        for (int j = left; j < right; j++) {
            // 频率高的元素排在前面
            if (nums.get(j)[1] >= pivot[1]) {
                i++;
                Collections.swap(nums, i, j);
            }
        }
        Collections.swap(nums, ++i, right);
        return i;
    }
}