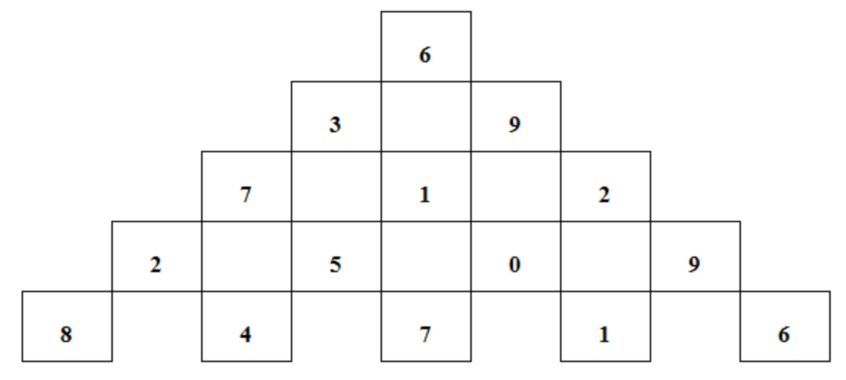
7-1 数塔
数塔如图所示,若每一步只能走到相邻的结点(图中有数字的方格),则从最顶层走到最底层所经过的所有结点的数字之和最大是多少?测试数据保证结果不大于231−1。
C++
#include <bits/stdc++.h>
using namespace std;
int main(){
int n;
cin>>n;
while(n--){
int a[101][101]={0};
int dp[101][101]={0};
int high;//最高层号
cin>>high;
for(int i=1;i<=high;i++){
for(int j=1;j<=i;j++){
cin>>a[i][j];
if(i==high){
dp[i][j]=a[i][j];//递推边界
}
}
}
for(int i=high-1;i>=1;i--){
for(int j=1;j<=i;j++){
dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+a[i][j];
}
}
cout<<dp[1][1]<<endl;
}
}
7-2 最大子列和问题
给定K个整数组成的序列{ N1, N2, ..., NK },“连续子列”被定义为{ Ni, Ni+1, ..., Nj },其中 1≤i≤j≤K。“最大子列和”则被定义为所有连续子列元素的和中最大者。例如给定序列{ -2, 11, -4, 13, -5, -2 },其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序,计算给定整数序列的最大子列和。
本题旨在测试各种不同的算法在各种数据情况下的表现。各组测试数据特点如下:
- 数据1:与样例等价,测试基本正确性;
- 数据2:102个随机整数;
- 数据3:103个随机整数;
- 数据4:104个随机整数;
- 数据5:105个随机整数;
输入格式:
#include<iostream>
using namespace std;
int main() {
int K, sum = 0;
int number[100000];
cin >> K;
for (int i = 0; i < K; i++) {
cin >> number[i];
}
for (int i = 0; i < K; i++) {
int temp = 0;
for (int j = i; j < K; j++) {
temp += number[j];
if (temp > sum) {
sum = temp;
}
}
}
cout << sum;
return 0;
}7-3 最长公共子序列
给定两个长度分别为 N 和 M 的字符串 A 和 B,求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。
#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];
int main() {
cin >> n >> m >> a + 1 >> b + 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (a[i] == b[j]) {
//找到一个公共字符,故长度加1
f[i][j] = f[i - 1][j - 1] + 1;
} else {
//没找到则找到临近最大的一个长度,表示最大长度还没有变化
//【为什么只需要找临近呢?因为dp数组中抽象地保存之前的状态,所以已经包含前面比较短的情况,再者,因为保存之前的状态,现在遍历到的这个位置,临近的元素就是之前状态的长度,因为我现在需要长度不变,所以在临近找一个最大的即可。】
f[i][j] = max(f[i - 1][j], f[i][j - 1]);
}
}
}
cout << f[n][m] << '\n';
return 0;
}7-4 jmu-ds-最长公共子串
给出2个字符串,输出2字符串的最长公共子串。
输入格式:
输入2个字符串,不可包含空格。
输出格式:
输出2个字符串的最长公共子串。若没有公共子串,则输出“NULL”
python
a = input()
b = input()
def maxSubstring(a,b):
if a==None or b==None:#空值返回
return None
#接下来获取两者较长和较短的字符串
if len(a)>len(b):
M=a
m=b
else:
M=b
m=a
#遍历遍历较短的字符串,并依次减少短字符串的字符数量,
#判断长字符是否包含该子串
i=0
while i<len(m):
begin=0
end=len(m)-i
#先扣住end部分的字符,然后一个循环看begin从0~end是否有符合的最大串
while end<=len(m):
current=m[begin:end]
if current in M:
return current
begin+=1
end+=1
i+=1
return 'NULL'
print(maxSubstring(a,b))
7-5 最长有序子序列
对于给定一个数字序列 (a1,a2,…,an) ,如果满足a1<a2<…<an,则称该序列是有序的。若在序列(a1,a2,…,an) 中删除若干元素得到的子序列是有序的,则称该子序列为一个有序子序列。有序子序列中长度最大的即为最长有序子序列。
例如,(1,3,5)、(3,5,8)、(1,3,5,9)等都是序列 (1,7,3,5,9,4,8) 的有序子序列;而(1,3,5,9)、(1,3,5,8)、(1,3,4,8)都是序列 (1,7,3,5,9,4,8)的一个最长有序子序列,长度为4。
请编写程序,求出给定数字序列中的最长有序子序列的长度。
python
def longest_ordered_subsequence(nums):
# 获取数字序列的长度
n = len(nums)
# 创建一个数组来保存以每个元素结尾的最长有序子序列的长度
dp = [1] * n
# 计算最长有序子序列的长度
for i in range(1, n):
for j in range(i):
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j] + 1)
# 返回最长有序子序列的最大长度
return max(dp)
# 读取输入数据的数量
T = int(input())
for _ in range(T):
# 读取数字序列的长度和元素
n = int(input())
sequence = list(map(int, input().split()))
# 计算并输出最长有序子序列的长度
result = longest_ordered_subsequence(sequence)
print(result)
# 输出空行(除了最后一组测试数据)
if _ != T - 1:
print()
7-6 跳房子
跳房子是小朋友玩的游戏。地面上画出一连串格子,每个格子里有一个整数,小朋友从外面跳入格子,并继续往前跳,直到跳出所有格子。每次跳跃的规则是,可以跳入下一格或下下格或下下下格。怎么跳能让落脚格子里的数的累加和最小。
python3
n = int(input()) # 读入格子数
nums = list(map(int, input().split())) # 读入每个格子里的数
nums=nums+[0]
dp = [100000] * (n + 2) # 初始化dp数组
dp[0] = 0
dp[1] = nums[0]
for i in range(2, n + 2 ):
dp[i] = min(dp[i - 1] + nums[i-1], dp[i - 2] + nums[i-1], dp[i - 3] + nums[i-1]) # 计算当前格子的最小累加和
print(dp[n+1]) # 输出结果
7-7 寻宝路线
在一个m行n列方格矩阵中,每一个方格内摆放着价值不等的宝贝(价值可正可负),让小明感到好奇的是,从左上角到达右下角的所有可能路线中,能捡到宝贝的价值总和最大是多少?而且这种达到最大值的路线
又有多少条?【注意:只能从一个格子向下或向右走到相邻格子,并且走到的格子宝贝一定会被捡起。】
c++
#include <iostream>
#include <vector>
using namespace std;
int main() {
int m, n;
cin >> m >> n;
vector<vector<int>> grid(m, vector<int>(n, 0));
// 读取宝贝价值矩阵
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
cin >> grid[i][j];
}
}
// 创建动态规划所需的二维数组
vector<vector<int>> dp(m, vector<int>(n, 0));
vector<vector<int>> ways(m, vector<int>(n, 0));
dp[0][0] = grid[0][0];
ways[0][0] = 1;
// 初始化第一列和第一行
for (int i = 1; i < m; ++i) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
ways[i][0] = 1;
}
for (int j = 1; j < n; ++j) {
dp[0][j] = dp[0][j - 1] + grid[0][j];
ways[0][j] = 1;
}
// 计算其余位置的最大值和路径数量
for (int i = 1; i < m; ++i) {
for (int j = 1; j < n; ++j) {
if (dp[i - 1][j] > dp[i][j - 1]) {
dp[i][j] = dp[i - 1][j] + grid[i][j];
ways[i][j] = ways[i - 1][j];
} else if (dp[i - 1][j] < dp[i][j - 1]) {
dp[i][j] = dp[i][j - 1] + grid[i][j];
ways[i][j] = ways[i][j - 1];
} else {
dp[i][j] = dp[i - 1][j] + grid[i][j];
ways[i][j] = ways[i - 1][j] + ways[i][j - 1];
}
}
}
int max_value = dp[m - 1][n - 1];
int max_ways = ways[m - 1][n - 1];
cout << max_value << " " << max_ways << endl;
return 0;
}
7-8 硬币找零
用 n 种不同币值的硬币凑出 m 元,最少需要多少硬币。
输入格式:
第一行输入需要凑的钱数 m 和硬币的种类 n (0<m<100,0<n<10),第二行输入 n 种硬币的具体币值,假设硬币供应量无限多。
输出格式:
输出最少需要的硬币个数
输入样例:
在这里给出一组输入。例如:
PYTHON3
def min_coins(coins, m):
dp = [float('inf')] * (m + 1)
dp[0] = 0
for i in range(1, m + 1):
for coin in coins:
if i >= coin:
dp[i] = min(dp[i], dp[i - coin] + 1)
return dp[m] if dp[m] != float('inf') else -1
if __name__ == "__main__":
m, n = map(int, input().split())
coins = list(map(int, input().split()))
result = min_coins(coins, m)
print(result)
7-9 至多删三个字符
给定一个全部由小写英文字母组成的字符串,允许你至多删掉其中 3 个字符,结果可能有多少种不同的字符串?
C++
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 10;
int dp[N][4];
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
string s, stemp;
cin >> stemp;
s.assign("0");
s.append(stemp);
dp[0][0] = 1;
for (int i = 1; i < s.size(); ++i)
{
for (int j = 0; j <= 3; ++j)
{
dp[i][j] = dp[i - 1][j];
if (j)
dp[i][j] = dp[i][j] + dp[i - 1][j - 1];
for (int k = i - 1; k >= 1 && i - k <= j; --k)
{
if (s[k] == s[i])
{
dp[i][j] = dp[i][j] - dp[k - 1][j - (i - k)];
break;
}
}
}
}
int ans = 0;
for (int i = 0; i <= 3; ++i)
{
ans = ans + dp[s.size() - 1][i];
}
cout << ans << endl;
return 0;
}
7-10 拼题A打卡奖励
拼题 A 的教超搞打卡活动,指定了 N 张打卡卷,第 i 张打卡卷需要 mi 分钟做完,完成后可获得 ci 枚奖励的金币。活动规定每张打卡卷最多只能做一次,并且不允许提前交卷。活动总时长为 M 分钟。请你算出最多可以赢得多少枚金币?
输入格式:
输入首先在第一行中给出两个正整数 N(≤103) 和 M(≤365×24×60),分别对应打卡卷的数量和以“分钟”为单位的活动总时长(不超过一年)。随后一行给出 N 张打卡卷要花费的时间 mi(≤600),最后一行给出 N 张打卡卷对应的奖励金币数量 ci(≤30)。上述均为正整数,一行内的数字以空格分隔。
C++
#include<bits/stdc++.h>
using namespace std;
const int N=1004;
const int INF=0x3f3f3f3f;
int n,m;
int w[N],v[N];
//int f[N][10000];
int dp[N][30005];//前i个物品中得到价值为j时候的最小花费 //ans为dp[n][j]<m时最大的j
int mv=0;
int main()
{
// cout<<365*60*24;
cin>>n>>m;
for(int i=1;i<=n;++i)cin>>w[i];
for(int i=1;i<=n;++i){
cin>>v[i];
mv+=v[i];
}
// 01背包写法,空间不够,而且也会超时,因为“花费”这一维度规模比较大,而递推时需要一一枚举
// for(int i=1;i<=n;++i)
// for(int j=0;j<=m;++j)
// {
// if(j>=w[i])
// f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]);
// else f[i][j]=f[i-1][j];
// }
//下面是另一种思路,第二维换成价值
//初始化
for(int i=0;i<=n;++i)
{
for(int j=0;j<=mv;++j){
dp[i][j]=INF;
}
}
dp[0][0]=0;
//递归过程:分为取第i个和不取第i个
for(int i=1;i<=n;++i)
{
for(int j=0;j<=mv;++j){
if(j>=v[i])//注意边界
dp[i][j]=min(dp[i-1][j-v[i]]+w[i],dp[i-1][j]);
else
dp[i][j]=dp[i-1][j];
}
}
//可以改进递推过程:由于递归方程中两个来源都是上一个i的,去掉第一个维度,节省空间,注意这时候j要从大到小迭代,才能保证递推过程中的dp[j-v[i]]是来源于i-1而不是i
// for(int i=1;i<=n;++i)
// {
// for(int j=mv;j>=0;--j)
// {
// if(j>v[i])
// dp[j]=min(dp[j-v[i]]+w[i],dp[j]);
// else
// dp[j]=dp[j];
// }
//取答案:最小花费在给定的m内的最大价值
for(int j=mv;j>=0;j--)
{
if(dp[n][j]<=m){
cout<<j;
break;
}
}
// cout<<f[n][m];
return 0;
}