P1825 [USACO11OPEN]Corn Maze S

(1条消息) P1825 [USACO11OPEN]Corn Maze S_lxh0113的博客-CSDN博客

然后下面是学到的知识：

之前学习算法的时候总是牵扯到图，但是关于图的一些知识并没有了解。下面是有关图的基础知识。

图的一些基础知识

图可以分为有向图和无向图

有向图：无向图：

（有向图指的就是有方向的图，由（无向图是没有方向的，图中1可以到

图中，我们可知1能到2，而2是不 2，而2也可以到1）

能到1的）

图还可以分为带权图和不带权图：

上面我所说的俩个都是带权图，下面这个是不带权图，就是它的连接的那条边，是没有权值的，这个权值可以是距离、时间、金钱等。

邻接矩阵

我们通常用二维数组来表示图，这种表示方法叫做邻接矩阵

比如下面的这张图：我们用权值表示可以到该点，通常用行标表示出发地，列标表示目的地，所以该数组a[1][2]的值表示5，即为可以到达，权值为5。通常我们把自己到自己那一条对角线全部设置为0。对于不能直接到达的，我们通常设置为∞，在代码中是没有无穷这个表达方式的，所以在代码中我们会定义INF给一个具体的很大的值，可以是int的最大边界值。对于无向图来说，邻接矩阵是沿着对角线对称的。

另外对于不带权图，我们用0 1表示可不可以到达，通常自己到自己设置为0（当然你喜欢的话是可以用1的）。

邻接表

用数组和链表或者指针数组存储的方式叫做邻接表。前面的那一列是为表头，是一个节点数组，后面的是链表或者指针数组表示可以连接的节点，我们可以在链表中存储节点名称以及权值都是可以的。

图还可以根据边与顶点的关系分为稀疏图和稠密图。

如果边小于顶点的平方，我们称之为稀疏图，如果大于等于称之为稠密图。

邻接表通常用来表示稀疏图，而邻接矩阵用来表示稠密图。

我写了关于邻接矩阵和邻接表的代码：

#include<stdio.h>
#include<malloc.h>
#define N 100
#define MAX 999999
int u[N],v[N],w[N],e[N][N];
int m,n;
typedef struct node
{
	int a;
	int x;
	struct node *next;
}NODE;
NODE k[N];
int fun()
{
	int i,j;
	NODE *p,*q;
	for(i=0;i<n;i++)
	{
		k[i].a=i+1;
		p=q=k+i;
		for(j=0;j<m;j++)
		{
			if(u[j]==k[i].a)
			{
				p=(NODE *)malloc(sizeof(NODE));
				p->a=v[j];
				p->x=w[j];
				q->next=p;
				q=q->next;
			}
			p->next=NULL;
		}
	}
}
int put(NODE *head)
{
	printf("%d",head->a);
	head=head->next;
	while(head)
	{
		printf("->%d(%d)",head->a,head->x);
		head=head->next;
	}
	puts("");
}
int main()
{
	int i,j;
	puts("请输入顶点数量：");
	scanf("%d",&n);
	puts("请输入边的数量：");
	scanf("%d",&m);
	for(i=0;i<n;i++)
	{
		for(j=0;j<n;j++)
		{
			if(i==j) e[i][j]=0;
			else e[i][j]=MAX;
		}
	}
	for(i=0;i<m;i++)
	{
		scanf("%d%d%d",&u[i],&v[i],&w[i]);
		e[u[i]-1][v[i]-1]=w[i];
	}
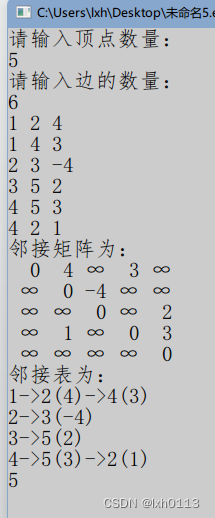
	puts("邻接矩阵为：");
	for(i=0;i<n;i++)
	{
		for(j=0;j<n;j++)
			if(e[i][j]!=MAX) printf("%3d",e[i][j]);
			else printf("%3s","∞");
		puts("");
	}
	fun();
	puts("邻接表为：");
	for(i=0;i<n;i++)
	{
		put(k+i);
	}
	return 0;
}

根据该图输入的