HashMap源码解析-jdk1.8（三）

负载因子loadFactor为什么是0.75？

/**
 * 默认的负载因子，用来衡量HashMap满的程度。
 */
static final float DEFAULT_LOAD_FACTOR = 0.75f;

负载因子，用来衡量HashMap满的程度。通常，默认负载因子（0.75）在时间和空间成本之间提供了一个很好的权衡。负载因子越大则散列表的装填程度越高，减少空间开销，但会增加查找成本。负载因子越小则链表中的数据量就越稀疏，此时会对空间造成烂费，但是此时索引效率高。

试想一下，如果我们把负载因子设置成1，容量使用默认初始值16，那么表示一个HashMap需要在"满了"之后才会进行扩容。那么在HashMap中，最好的情况是这16个元素通过hash算法之后分别落到了16个不同的桶中，否则就必然发生哈希碰撞。而且随着元素越多，哈希碰撞的概率越大，查找速度也会越低。

我们假设一个bucket空和非空的概率为0.5，我们用s表示容量，n表示已添加元素个数。用s表示添加的键的大小和n个键的数目。根据二项式定理，桶为空的概率为:

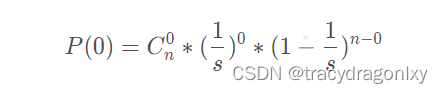
因此，如果桶中元素个数小于以下数值，则桶可能是空的：

当s趋于无穷大时，如果增加的键的数量使P(0) = 0.5，那么n/s很快趋近于ln(2)（约等于0.6931…），所以，合理值大概在0.7左右。

通过一个数学推理，测算出这个数值在0.7左右是比较合理的。那么，为什么最终选定了0.75呢？还记得前面我们提到过一个公式吗，就是临界值（threshold） = 负载因子（loadFactor） * 容量（capacity）。其中capacity的值永远都是2的幂，为了保证threshold是一个整数，这个值是0.75(3/4)比较合理，因为这个数和任何2的幂乘积结果都是整数。

数组桶中的链表长度大于8就会转化为红黑树，既然转化为红黑树，那么treeNode占用的空间就是普通链表Node占用空间的两倍大，这样空间上会造成损失，为了避免这样的损失，经过研究计算发现，在随机hash的时候，数组桶内的Node元素分布呈现泊松分布。既然是泊松分布，那么我们就需要一个阈值，尽可能的避免treeNode的出现，这时候负载因子出场了，负载因子为0.75的时候，桶中的Node的分布频率服从参数为0.5的泊松分布。桶内达到8以上的元素几乎不可能（一亿分之6的概率），这样就避免了TreeNode的出现。

• 0: 0.60653066
• 1: 0.30326533
• 2: 0.07581633
• 3: 0.01263606
• 4: 0.00157952
• 5: 0.00015795
• 6: 0.00001316
• 7: 0.00000094
• 8: 0.00000006
• more: less than 1 in ten million

当桶中元素到达8个的时候，概率已经变得非常小，也就是说用0.75作为加载因子，每个碰撞位置的链表长度超过8个是几乎不可能的。

HashMap的长度为什么是2的幂次方

1. 与取余等价的算法

为了能让 HashMap 存取高效，尽量较少碰撞，也就是要尽量把数据分配均匀。为了减少hash值的碰撞，需要实现一个尽量均匀分布的hash函数，在HashMap中通过利用key的hashcode值，来进行位运算。

这里的Hash算法本质上就是三步：取key的hashCode值、高位运算、取模运算。

/*
 * jdk1.8 & jdk1.7
 * 从速度、功效、质量来考虑的，这么做可以在数组table的length比较小的时候，
 * 也能保证考虑到高低Bit都参与到Hash的计算中，同时不会有太大的开销。
 */
static final int hash(Object key) {
    int h;
    // h = key.hashCode() 为第一步 取hashCode值
    // h ^ (h >>> 16)  为第二步 高位参与运算
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

/*
 * jdk1.7的源码，jdk1.8没有这个方法，但是实现原理一样的
 */
 static int indexFor(int h, int length) { 
     return h & (length-1);  //第三步 取模运算
}

把hash值对数组长度取模运算，这样一来，元素的分布相对来说是比较均匀的。但是，模运算的消耗还是比较大的。h & (length-1)就是取模操作，Java之所有使用位运算(&)来代替取模运算(%)，最主要的考虑就是效率。位运算(&)效率要比代替取模运算(%)高很多，主要原因是位运算直接对内存数据进行操作，不需要转成十进制，因此处理速度非常快。

那么，为什么可以使用位运算(&)来实现取模运算(%)呢？这实现的原理如下：

取余(%)操作中如果除数是 2 的幂次则等价于与其除数减一的与(&)操作（也就是说 hash % length == hash & (length-1)的前提是 length 是 2 的 n 次方），这就解释了 HashMap 的长度为什么是 2 的幂次方。

X % 2ⁿ = X & (2ⁿ - 1)
2ⁿ: 表示2的n次方，也就是说，一个数对2ⁿ取模 == 一个数和(2ⁿ - 1)做按位与运算 。
假设n为3，则2³ = 8，表示成2进制就是1000。2³ -1 = 7 ，即0111。
此时X & (2³ - 1) 就相当于取X的2进制的最后三位数。
从2进制角度来看，X / 8相当于 X >> 3，即把X右移3位，此时得到了X / 8的商，而被移掉的部分(后三位)，则是X % 8，也就是余数。

举个例子：

假如 length = 2⁴ = 16，二进制10000。这个数减去1的结果是1111，也就是length -1 = 1111。 （下面这段中的数字都是二进制） 再假设一个key的hash值为10011011001，与1111做 & 操作，得到的结果是1001（高位部分1001101都舍去了）。而1001必然是一个小于10000的数，对于一个小于10000的数而言，1001 % 10000得到的就是1001自己。

那么刚刚舍弃的高位部分1001101 0000（后面补上了四个0000）就一定能被10000整除吗？答案是肯定的：因为10011010000可以拆成10000000000+10000000+1000000+10000，这几个数都能通过10000的n次左移得到，也就相当于这几个数都能被10000整除。那他们的和，也就是10011010000，一定也可以被10000整除。 因此，最终结论就是：10011011001 & ( 10000 - 1 ) = 10011011001 & 1111 = 1001 = 10011011001 % 10000

2. 扩容时方便定位

当hashmap需要扩容，重新计算链表元素的hashcode，以进行元素的重新定位时，依然能从“ 数组2次幂 ”的这个设定中借力！ hashmap数组扩容时，新数组length = 原数组length * 2，沿用前面的例子（length = 2⁴ = 16，二进制10000），length 乘以 2 ,即二进制左移一位，由 10000 变成 100000。此时需要重新计算数组槽中的元素位置，如果槽中是链表，链表中每个元素都需要重新计算位置（这里不考虑红黑树）。

计算的公式不变，key.hashcode & (array.length - 1)，由于数组的翻倍（10000->100000），导致 array.length - 1 发生了改变（1111->11111）。此时，扩容前原本被舍弃的高位部分的最后1位，也将参与计算。

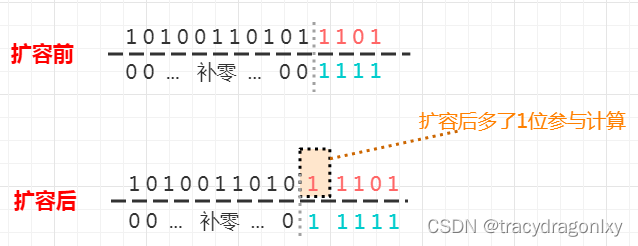
在扩容这里，这一位就显得很特别：如果这个位置是0，余数计算的结果将保持不变，意味着扩容后此元素还在这个槽中（槽编号没发生改变）；如果这个位置是1，余数计算结果就变成了原槽索引 + 原length。也就是说，hashmap扩容的元素迁移过程中，由于数组大小是2次幂的巧妙设定，使得只要检查 “ 特殊位 ” 就能确定该元素的最终定位。

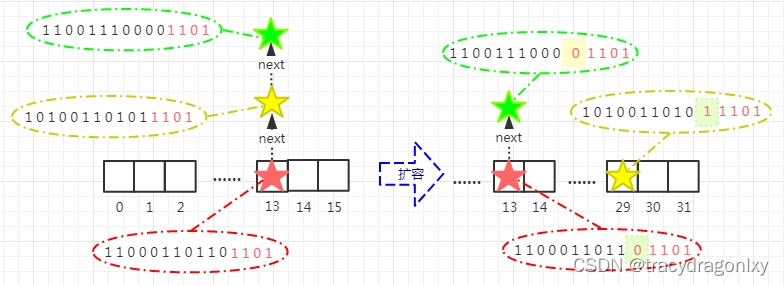
**扩容前：**红绿黄三个元素，由各自的hashcode取余后都淤积在数组槽13，组成链表形式。

**扩容后：**红、绿二星所表示的元素的hashcode“ 特殊位 ”为0，取余依然定位在槽13；而黄星表示的元素，hashcode“ 特殊位 ”为1，取余后结果 = 原槽索引 + 原数组大小 = 13 + 16 = 29。（这个结果也和图中黄星的hashcode二进制低位值11101一致）。

总结

对hashmap而言，数组长度始终保持2次幂有两点好处：

1. 能利用 & 操作代替 % 操作，提升性能
2. 数组扩容时，仅仅关注 “特殊位” 就可以重新定位元素

参考：
https://stackoverflow.com/questions/10901752/what-is-the-significance-of-load-factor-in-hashmap
http://hollischuang.gitee.io/tobetopjavaer/#/basics/java-basic/hash-in-hashmap