数据结构第五课 -----二叉树的代码实现

news2024/11/26 23:40:03

作者前言

🎂 ✨✨✨✨✨✨🍧🍧🍧🍧🍧🍧🍧🎂
​🎂 作者介绍： 🎂🎂
🎂 🎉🎉🎉🎉🎉🎉🎉 🎂
🎂作者id：老秦包你会， 🎂
简单介绍：🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂🎂
喜欢学习C语言和python等编程语言，是一位爱分享的博主，有兴趣的小可爱可以来互讨 🎂🎂🎂🎂🎂🎂🎂🎂
🎂个人主页::小小页面🎂
🎂gitee页面:秦大大🎂
🎂🎂🎂🎂🎂🎂🎂🎂
🎂 一个爱分享的小博主 欢迎小可爱们前来借鉴🎂

二叉树的顺序结构实现

  • **作者前言**
  • 小知识
  • 堆的实现
    • 结构体
    • 插入
    • 删除
    • 根节点
    • 长度
    • 是否为空
  • TOP-K问题
  • 堆排序
  • 总结

小知识

完全二叉树的堆的创建时间复杂度
假设我们随意给出一个长度为n的数组，如果我们要建堆，最坏的情况就是全部节点都要向下调整
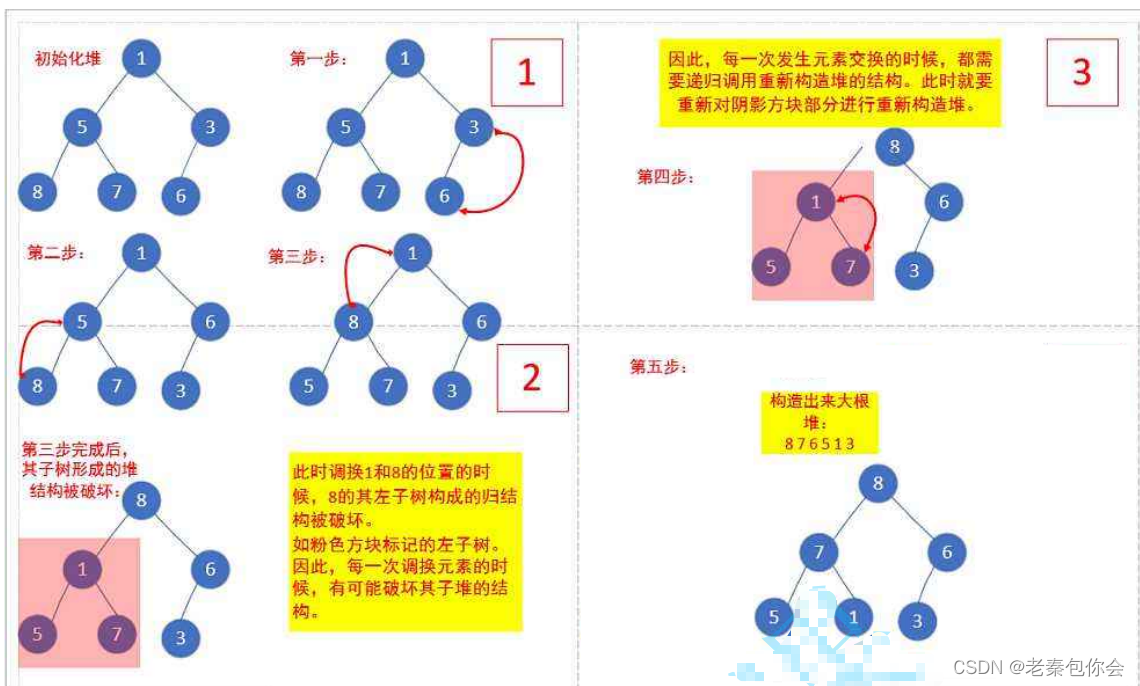
在这里插入图片描述
我们可以当完全二叉树是满二叉树进行计算
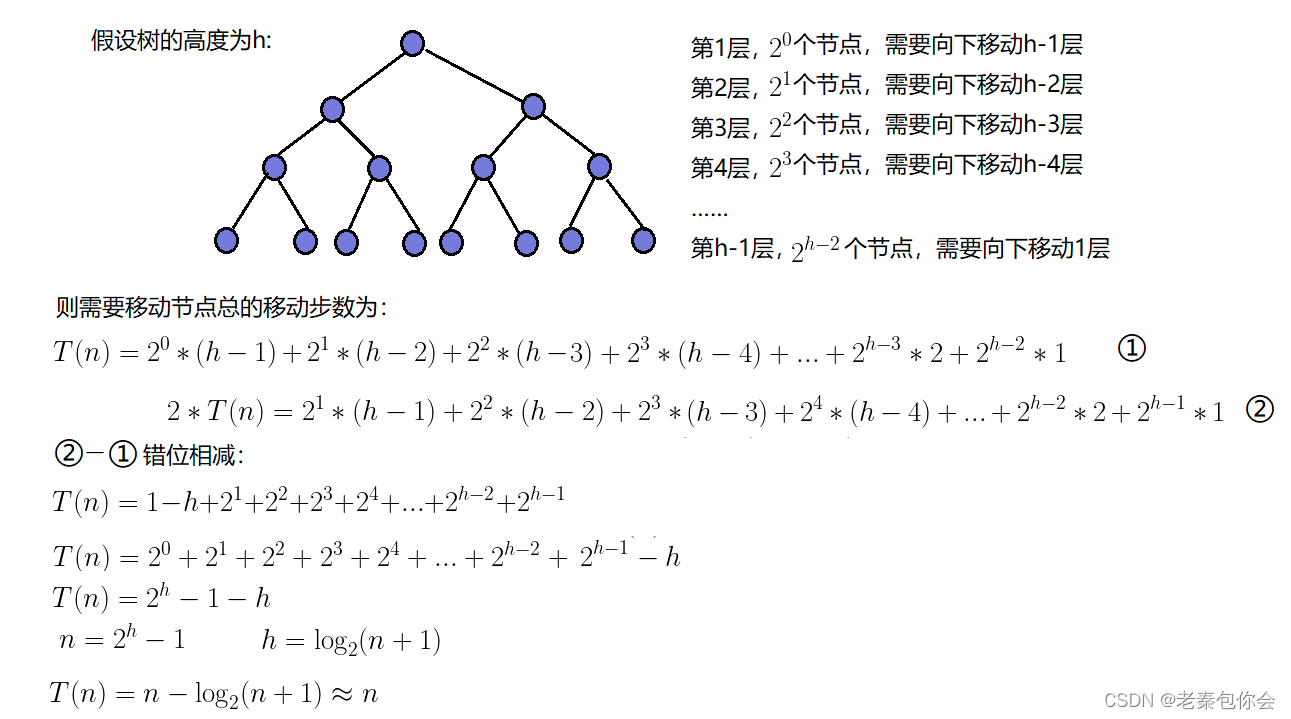
在这里插入图片描述
我们需要统计全部节点的移动次数，最终全部计算出 2^h -1 - h,因为是每个节点要往下移动一个高度次, 满二叉树是 的节点数 N = 2 ^h - 1 所以 h = log(N +1),代入 2^h -1 - h得出n - log(n+1) 大约就是n次 而每个节点的时间复杂度是大约是O(log(N))(每个节点向下调整高度次).这个就是向下调整的时间复杂度O(N)

向上调整的时间复杂度
二叉树的最后一层占据所有节点的一半

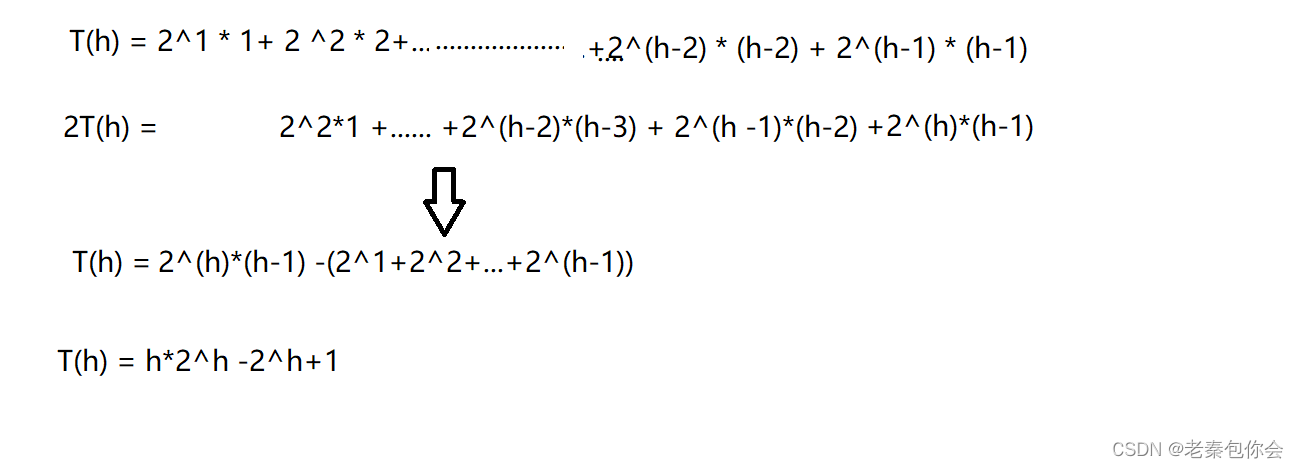
在这里插入图片描述
最终化简就是T(n) = (n+1)*(log(n+1) - 1) +1 -n 大概就是O(N *log(N))

堆的实现

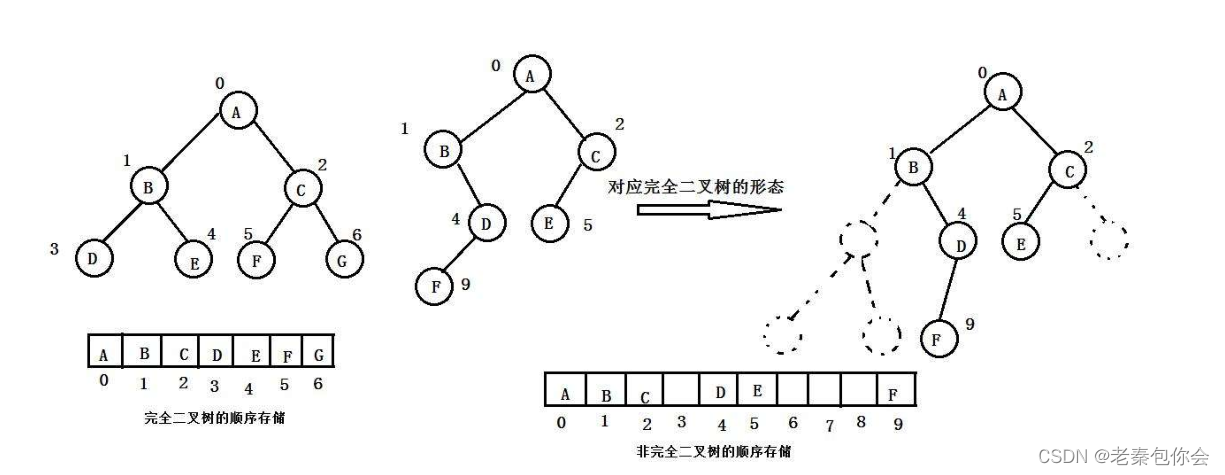
在这里插入图片描述
可以发现我们的要想实现二叉树就得借助顺序表来进行操作，因为二叉树是逻辑结构，我们要想实现就得利用物理结构，也就是堆 ，堆有大小堆的区分，下面我以小堆来实现

结构体

在这里插入图片描述
这里是利用顺序表来存储,所以结构和顺序表是一样的,但是本质上还是二叉树

typedef int HDataType;
typedef struct Heap
{
	HDataType* tree;
	int size;
	int capacity;
}Heap;

插入

思路：我们先插入最后一个，然后向上调整，因为我们是小堆，要保证每个父亲<= 孩子
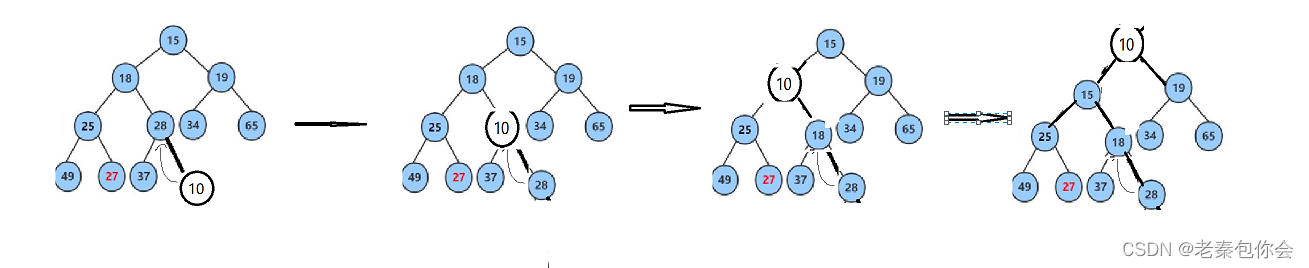
在这里插入图片描述
这里我们要注意不能越界,

//向上调整
void adjust(HDataType* tree, int Hsize)
{
	int child = Hsize - 1;
	int parent = (Hsize - 1 - 1) / 2;
	while (child > 0)
	{
		if (tree[child] < tree[parent])
		{
			HDataType b = tree[child];
			tree[child] = tree[parent];
			tree[parent] = b;
			child = parent;
			parent = (child - 1) / 2;
		}
		else
			return;
	}
}
// 插入
void Heappush(Heap* obj, HDataType elemest)
{
	//判断释放满
	if (obj->size == obj->capacity)
	{
		obj->capacity = (obj->capacity == 0 ? 4 : obj->capacity * 2);
		HDataType * tmp = realloc(obj->tree, sizeof(Heap) * obj->capacity);
		if (tmp == NULL)
		{
			perror("realloc");
			return;
		}
		obj->tree = tmp;
	}
	obj->tree[obj->size++] = elemest;
	//开始检查是否大于父节点
	adjust(obj->tree, obj->size);
	
}

我们主要就是考虑 根节点和自己的孩子这里,是有可能越界的
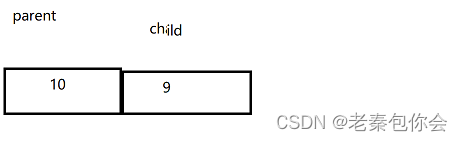
在这里插入图片描述

如图,可以利用child == 0来结束,

删除

这里的删除和前面我们学习过的顺序表和链表的删除不太一样,这里的删除是要删除二叉树的根节点，删除后又要构成一样的小堆
思路： 根节点和最后一个叶节点进行交换，然后删除叶节点（新的叶节点），交换后的根节点（新的根节点），然后让左右孩子进行比较大小，比较出最小值，然后再和根节点进行比较，如果根节点大于，就交换，然后依次循环直到符合小堆， 如果小于或者等于则不用调整，但是因为我们是把最后一个叶节点交换，交换的节点可能会大于等于，这种情况可以忽略，但是思路还是可以借鉴，
需要注意的是我们交换是循环进行的要找到结束条件

// 删除 (删除根节点)
void HeapPop(Heap* obj)
{
	assert(obj);
	assert(obj->size > 0);
	//两节点交换
	HDataType elemest = obj->tree[0];
	obj->tree[0] = obj->tree[obj->size - 1];
	obj->tree[obj->size - 1] = elemest;
	obj->size--;
	//向下调整
	int parent = 0;
	int  child = parent * 2 + 1;
	if (parent * 2 + 1 < obj->size && parent * 2 + 2 < obj->size &&  obj->tree[parent * 2 + 1] > obj->tree[parent * 2 + 2] )
	{
		child = parent * 2 + 2;
	}
	while (child < obj->size)
	{
		
		//判断孩子和父亲的大小
		if (obj->tree[parent] > obj->tree[child])
		{
			//两节点交换
			HDataType elemest = obj->tree[parent];
			obj->tree[parent] = obj->tree[child];
			obj->tree[child] = elemest;
			parent = child;
		}
		else
			break;
		child = parent * 2 + 1;
		if (parent * 2 + 1 < obj->size && parent * 2 + 2 < obj->size && obj->tree[parent * 2 + 1] > obj->tree[parent * 2 + 2])
		{
			child = parent * 2 + 2;
		}

	}
	

}

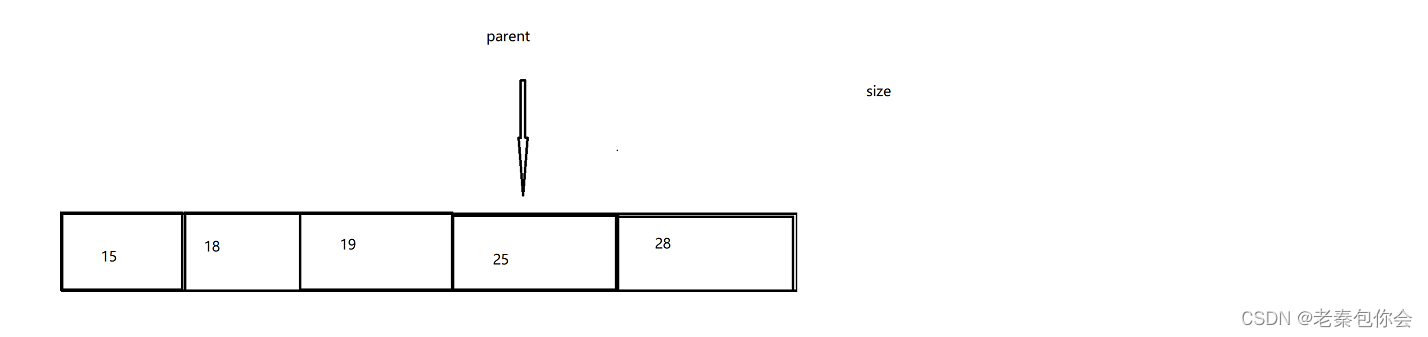
在这里插入图片描述
我们可以判断child是否大于等于size，，因为我们的思路就是要找到叶节点，我们只需child大于等于size就停止循环

根节点

// 根
HDataType  HeapTop(Heap* obj)
{
	assert(obj);
	assert(obj->size > 0);
	return obj->tree[0];
}

长度

// 长度
size_t HeapSize(Heap* obj)
{
	assert(obj);
	return obj->size;
}

是否为空

//是否为空
bool HeapEmpty(Heap* obj)
{
	assert(obj);
	return obj->size == 0;
}

TOP-K问题

TOP-K问题： 即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。
在N个数中找出前K个大的数(N远大于K)

  1. 思路: 把N个数创建成大堆,然后pop K次
    这种算法的时间复杂度是 N *log(N) + K *log(N),每个节点向下调整
    最终大约是O(N *log(N))
    这种算法还是有差异
    如果N是100亿, k = 10, 一个整形4个字节
    那么我们就需要400亿字节,也就大约40G内存,我们电脑内存最多就32G,这个方法行不通
  2. 思路:
    1.读取N个数的K个,创建一个K个数的小堆,
    2.然后依次把剩下的N-K个数进行和堆顶比较,如果大于堆顶就顶替堆顶,然后向下调整形成小堆,
    注意的是我们是要大于堆顶的数顶替原来的堆顶,不是让小的顶替, 我们知识借鉴了小堆的思路,并不是完全是按照小堆的思路走
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
void exchange(int *a, int *b)
{
	int e = *a;
	*a = *b;
	*b = e;
}
void PrintTop(int n)
{
	//创建一个n个数的小堆
	FILE* pf = fopen("./test.txt", "r");
	if (pf == NULL)
	{
		perror("fopen");
		return 1;
	}
	int* Heap = (int*)malloc(sizeof(int) * n);
	int i = 0;
	for (i = 0; i < n; i++)
	{
		int elemest;
		fscanf(pf, "%d", &elemest);
		Heap[i] = elemest;
		//向上调整
		int child = i;
		int parent = (child - 1) / 2;
		while (child > 0)
		{
			if (Heap[child] < Heap[parent])
			{
				exchange(&Heap[child], &Heap[parent]);
			}
			else
				break;
			child = parent;
			parent = (child - 1) / 2;

		}

	}
	// 继续读取下面的数据
	int ch = 0;
	while ( fscanf(pf, "%d", &ch) != EOF)
	{
		if (ch <= Heap[0])
		{
			continue;
		}
		Heap[0] = ch;
		//向下调整
		int parent = 0;
		int child = parent * 2 + 1;
		while (child < n)
		{
			if (child + 1 < n && Heap[child] > Heap[child + 1])
				{
					child += 1;
				}
			if (Heap[child] < Heap[parent])
				exchange(&Heap[child], &Heap[parent]);
			else
				break;
			parent = child;
			child = parent * 2 + 1;
		}

	}
	//打印数据
	for (i = 0; i < n; i++)
	{
		printf("%d ", Heap[i]);
	}
	free(Heap);
	fclose(pf);
}
void random(int n)
{
	FILE* pf = fopen("./test.txt", "w");
	if (pf == NULL)
	{
		perror("fopen");
		return 1;
	}
	srand(time(NULL));
	int i = 0;
	for (i = 0; i < 10000; i++)
	{
		fprintf(pf, "%d\n", (rand() + i) % 100000);
	}

	fclose(pf);
}

int main()
{
	int n = 10;

	PrintTop(n);



	return 0;
}

上面的代码中的建堆的代码可以使用插入小堆然后进行向上调整的方法,还有一种方法是假设一棵二叉树的
左右子树都是大堆或者小堆,然后我们只需进行根节点和左右子树点进行调整
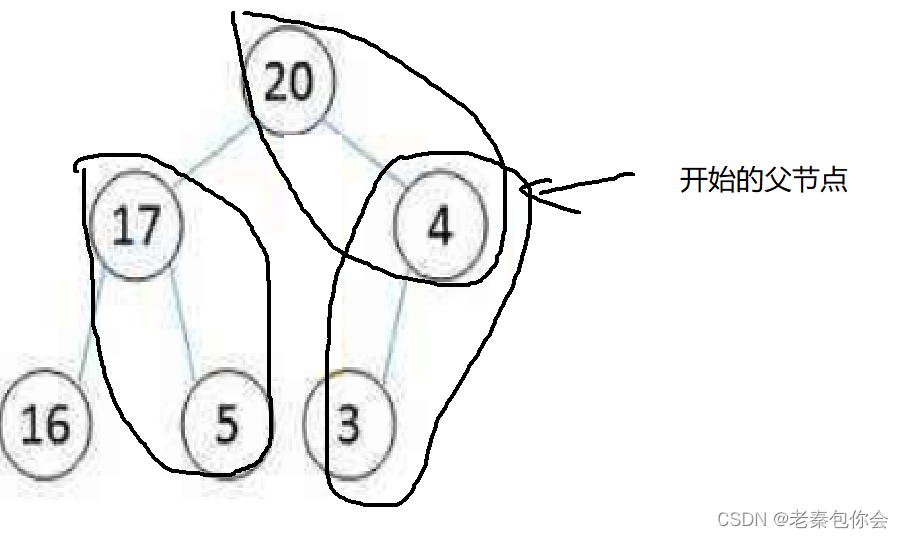
在这里插入图片描述
我们只需对最后叶节点的父节点开始进行向下调整,然后依次往下,

// 第二种方法
	//从最后一个节点的父亲开始向下调整,我们创建的是小堆 ,
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		//向下调整
		int parent = i;
		int child = parent * 2 + 1;
		while (child < n)
		{
			if (child + 1 < n && Heap[child] > Heap[child + 1])
			{
				child += 1;
			}
			if (Heap[child] < Heap[parent])
				exchange(&Heap[child], &Heap[parent]);
			else
				break;
			parent = child;
			child = parent * 2 + 1;
		}
	}

这种算法的效率更高,第一种方法是我们慢慢学习了堆总结出来的,先插入值进堆,然后向上调整,这样很蛮烦
但是这种方法从一开始就是左右子树就是大堆或者小堆,然后只需进行根节点的向下调整就可以,这个是递归思想的一种体现

堆排序

升序排序建大堆 ，降序排序建小堆
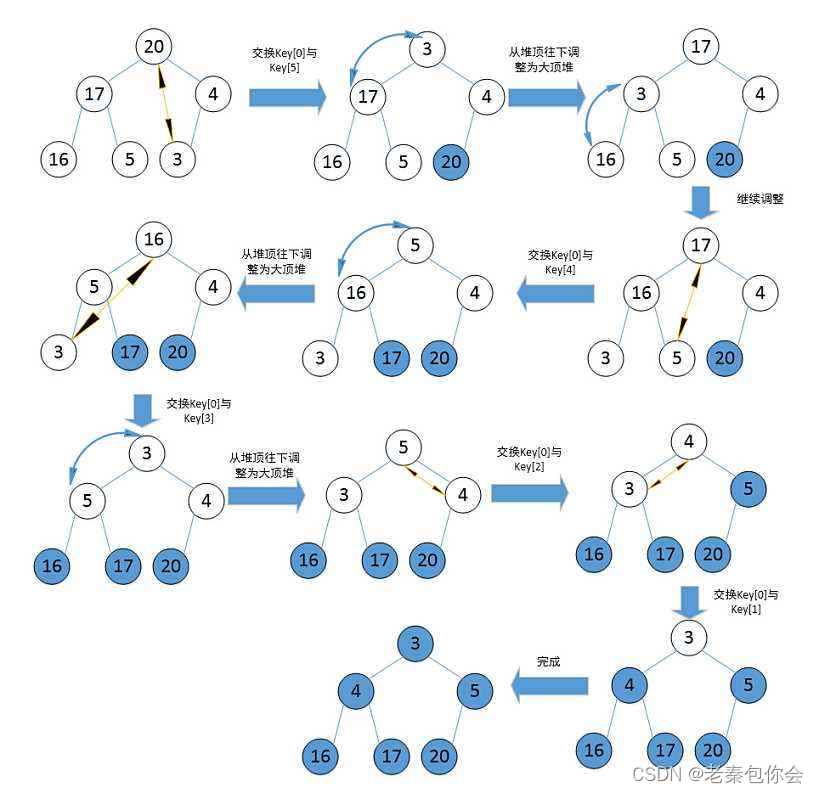
在这里插入图片描述

在这里插入图片描述
思路： 先 根节点和最后一个叶节点进行交换，这样就可以把最大的数放在数组的末尾，然后长度再减1
依次循环往下直到长度为1，或者下标为0就停止

#include<stdio.h>
typedef int Heapdata;
void exchange(Heapdata *a, Heapdata *b)
{
	Heapdata e = *a;
	*a = *b;
	*b = e;
}
void Heapsort(Heapdata* heap, int size)
{
	//建大堆
	int i = 0; 
	for (i = 1; i < size; i++)
	{
		//向上调整
		int child = i;
		int parent = (child - 1) / 2;
		while (child > 0)
		{
			if (heap[child] > heap[parent])
			{
				//交换
				exchange(&heap[child], &heap[parent]);
				child = parent;
				parent = (child - 1) / 2;
			}
			else
				break;
		}

	}
	//开始升序排序
	while (size > 0)
	{
		// 根节点和最后一个叶节点交换
		exchange(&heap[0], &heap[--size]);
		//向下调整
		int parent = 0;
		int child = parent * 2 + 1;
		while (child < size)
		{
			if (child + 1 < size && heap[child] < heap[child + 1])
			{
				child += 1;
			}
			if (heap[child] > heap[parent])
				exchange(&heap[child], &heap[parent]);
			else
				break;
			parent = child;
			child = parent * 2 + 1;
		}
	}
	


}
int main()
{
	Heapdata a[] = { 2,1,48,5,2,4,7,5,63,8 };
	int size = sizeof(a) / sizeof(a[0]);
	//堆排序
	Heapsort(a, size);


	return 0;
}

总结

这里简单介绍了堆 堆排序和Top K问题,还介绍了向下调整的时间复杂度和向上调整的时间复杂度

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1267236.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

代码混淆的原理和方法详解

代码混淆的原理和方法详解

代码混淆的原理和方法详解摘要移动App的广泛使用带来了安全隐患&#xff0c;为了保护个人信息和数据安全&#xff0c;开发人员通常会采用代码混淆技术。本文将详细介绍代码混淆的原理和方法&#xff0c;并探讨其在移动应用开发中的重要性。 引言随着移动应用的普及&#xff0c;…
阅读更多...
卷轴模式：金融领域的新趋势

卷轴模式：金融领域的新趋势

卷轴模式在金融领域逐渐崭露头角&#xff0c;成为一种新型的投资策略。这种模式基于完成任务或达成特定目标来获取积分&#xff0c;利用这些积分进行投资或获取现实物品。它不同于传统的资金盘&#xff0c;而是以一种更稳健的方式运作&#xff0c;避免了资金盘的风险。 一、卷轴…
阅读更多...
用BootLoader更新S32K144的固件

用BootLoader更新S32K144的固件

1、工具&#xff1a;MDK及S32K144的支持包 创芯科技的USB转CAN 及 驱动 Jlink烧写器及驱动 链接&#xff1a;https://pan.baidu.com/s/1jGRdGVEzrO86CpP5UQ2fYQ 提取码&#xff1a;nihd IAP固件升级上位机 2、BootLoader底层文件 a、用MDK打开BootLoader工程 b、更改配置…
阅读更多...
《golang设计模式》第三部分·行为型模式-09-策略模式（Strategy）

《golang设计模式》第三部分·行为型模式-09-策略模式（Strategy）

文章目录 1. 概述1.1 作用1.1 角色1.2 类图 2. 代码示例2.1 设计2.2 代码2.3 类图 1. 概述 1.1 作用 策略&#xff08;Strategy&#xff09;是用于封装一组算法中单个算法的对象&#xff0c;这些策略可以相互替换&#xff0c;使得单个算法的变化不影响使用它的客户端。 1.1 …
阅读更多...
C# API 文档自动生成器

C# API 文档自动生成器

文章目录 前言SandcastleDocFX 前言 最近要和别人交际&#xff0c;就要给API文档&#xff0c;但是感觉API文件手动写有点麻烦&#xff0c;想着怎么弄一个自动API文档生成 Sandcastle 折腾了两小时&#xff0c;好像不太好用 微软开源全新的文档生成工具DocFX DocFX 既然不好…
阅读更多...
私域流量灵魂三问

私域流量灵魂三问

私域流量灵魂三问: 1、是什么&#xff1f; 2、为什么做&#xff1f; 3、怎么做&#xff1f;
阅读更多...
嵌入式LCD软件驱动流程与调试

嵌入式LCD软件驱动流程与调试

前言 LCD屏在嵌入式中是应用比较广泛的&#xff0c;很多电子产品都是需要用到它来进行人机交互&#xff0c;那么工作中我们就少不了要对lcd进行软件驱动和调试。调试LCD需要掌握的学问有很多&#xff0c;没有一定的调试经验就很难对问题进行分析并解决。 博文推荐 LCD屏接口与…
阅读更多...
网络协议系列：TCP三次握手，四次挥手的全过程，为什么需要三次握手，四次挥手

网络协议系列：TCP三次握手，四次挥手的全过程，为什么需要三次握手，四次挥手

TCP三次握手&#xff0c;四次挥手的全过程&#xff0c;为什么需要三次握手&#xff0c;四次挥手 一. TCP三次握手&#xff0c;四次挥手的全过程&#xff0c;为什么需要三次握手&#xff0c;四次挥手前言TCP协议的介绍三次握手三次握手流程&#xff1a;1. A 的 TCP 向 B 发送 连…
阅读更多...
LVS-NAT实验

LVS-NAT实验

实验前准备&#xff1a; LVS负载调度器&#xff1a;ens33&#xff1a;192.168.20.11 ens34&#xff1a;192.168.188.3 Web1节点服务器1&#xff1a;192.168.20.12 Web2节点服务器2&#xff1a;192.168.20.13 NFS服务器&#xff1a;192.168.20.14 客户端&#xff08;win11…
阅读更多...
速速报名！请查收 2023 龙蜥操作系统大会超全指南

速速报名！请查收 2023 龙蜥操作系统大会超全指南

亲爱的小伙伴们&#xff0c;大家好&#xff01;我是大家的老朋友小龙&#xff01;自 2023 龙蜥操作系统大会宣布启动以来&#xff0c;小龙收到了来自四面八方的诸多期待和小心心。首届龙蜥大会正如火如荼地进行中&#xff0c;为表示对关注社区的每一位小伙伴由衷的感谢&#xf…
阅读更多...
排序算法基本原理及实现1

排序算法基本原理及实现1

&#x1f4d1;打牌 &#xff1a; da pai ge的个人主页 &#x1f324;️个人专栏 &#xff1a; da pai ge的博客专栏 ☁️宝剑锋从磨砺出&#xff0c;梅花香自苦寒来 &#x1f4d1;插入排序 &#x1f4…
阅读更多...
人工智能即将彻底改变你使用计算机的方式

人工智能即将彻底改变你使用计算机的方式

文章目录 每个人的私人助理“Clippy 是一个机器人&#xff0c;而不是特工。”卫生保健“一半需要心理健康护理的美国退伍军人没有得到治疗。”教育生产率娱乐和购物科技行业的冲击波技术挑战隐私和其他重大问题 今天我仍然像保罗艾伦和我创办微软时一样热爱软件。但是&#xff…
阅读更多...
Linux系统之一次性计划任务at命令的基本使用

Linux系统之一次性计划任务at命令的基本使用

Linux系统之一次性计划任务at命令的基本使用 一、at命令介绍二、at命令的使用帮助2.1 at命令的help帮助信息2.2 at命令的语法解释 三、at命令的日常使用3.1 立即执行一次性任务3.2 指定时间执行一次性任务3.3 查询计划任务3.4 其他指定时间用法3.5 删除已经设置的计划任务3.6 显…
阅读更多...
C语言——计算Fibonacci数列

C语言——计算Fibonacci数列

方式一 for循环 (20位) #define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h> int main() {int n;int a[20]{1,1};for ( n 1; n <20; n){a[n]a[n-2]a[n-1];}for ( n 0; n < 20; n){if(n%50)printf("\n");printf("%12d ",a[n]);}return 0; …
阅读更多...
【每日一题】无限集中的最小数字

【每日一题】无限集中的最小数字

文章目录 Tag题目来源题目解读解题思路方法一&#xff1a;有限集合方法二&#xff1a;有序集合 写在最后 Tag 【有序集合】【2023-11-29】 题目来源 2336. 无限集中的最小数字 题目解读 设计一个类实现移除无限集中的最小整数以及向该无限集中增加一个原集合中不存在的整数。…
阅读更多...
【JavaEE初阶】 HTTP响应报文

【JavaEE初阶】 HTTP响应报文

文章目录 &#x1f332;序言&#x1f38d;200 OK&#x1f340;404 Not Found&#x1f384;403 Forbidden&#x1f334;405 Method Not Allowed&#x1f38b;500 Internal Server Error&#x1f333;504 Gateway Timeout&#x1f332;302 Move temporarily&#x1f38d;301 Move…
阅读更多...
vs2012切换版本后WebUI项目加载失败，右键重新加载提示已经在解决方案中打开了具有该名称的项目

vs2012切换版本后WebUI项目加载失败，右键重新加载提示已经在解决方案中打开了具有该名称的项目

问题描述 vs2012切换版本后&#xff0c;回到主版本web项目加载失败&#xff0c;右键重新加载提示已经在解决方案中打开了具有该名称的项目 解决办法 打开根目录.csproj文件&#xff0c;找到第一个ProectTypeGuides节点&#xff0c;删除掉。然后关闭vs,重新打开此项目即可。这…
阅读更多...
rust-flexi_logger

rust-flexi_logger

flexi_logger 是字节开源的rust日志库。目前有log4rs、env_log 等库&#xff0c;综合比较下来&#xff0c;还是flexi_logger简单容易上手&#xff0c;而且自定义很方便&#xff0c;以及在效率方面感觉也会高&#xff0c;下篇文章我们来测试下。 下面来看下怎么使用 关注 vx gol…
阅读更多...
bugku题解记录2

bugku题解记录2

文章目录 哥哥的秘密黄道十二官where is flag一段新闻 哥哥的秘密 给出了一个qq&#xff0c;那就去看看呗 hint里面说 收集空间信息——相册——收集微博信息——相册——解题——相册——提交flag 那看看空间先 盲文&#xff1a; hint&#xff1a;密码时地人 旗帜存在相册里…
阅读更多...
Nature子刊最新研究：Hi-C宏基因组揭示土壤-噬菌体-宿主相互作用

Nature子刊最新研究：Hi-C宏基因组揭示土壤-噬菌体-宿主相互作用

土壤中有大量的噬菌体。然而&#xff0c;大多数宿主未知&#xff0c;无法获得其基因组特征。2023年11月23日&#xff0c;最新发表于《Nature communications》期刊题为“Hi-C metagenome sequencing reveals soil phage–host interactions”的文章&#xff0c;通过高通量染色体…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023