线性回归
- 回归处理的问题为预测:
- 预测房价
- 销售额的预测
- 设定贷款额度
- 总结:上述案例中,可以根据事物的相关特征预测出对应的结果值
什么是回归
那么,这个回归究竟是什么意思呢?其实回归算法是相对分类算法而言的,与我们想要预测的目标变量y的值类型有关。如果目标变量y是分类型变量,如预测用户的性别(男、女),预测月季花的颜色(红、白、黄……),预测是否患有肺癌(是、否),那我们就需要用分类算法去拟合训练数据并做出预测;
如果y是连续型变量,如预测用户的收入(4千,2万,10万……),预测员工的通勤距离(500m,1km,2万里……),预测患肺癌的概率(1%,50%,99%……),我们则需要用回归模型。
一元线性回归
线性回归可以说是用法非常简单、,作为机器学习的入门算法非常合适。我们上中学的时候,都学过二元一次方程,我们将y作为因变量,x作为自变量,得到方程:
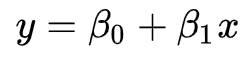
当给定参数β0和β1的时候,画在坐标图内是一条直线(这就是“线性”的含义)。
当我们只用一个x来预测y,就是一元线性回归,也就是在找一个直线来拟合数据。
比如,我有一组数据画出来的散点图,横坐标代表广告投入金额,纵坐标代表销售量,线性回归就是要找一条直线,并且让这条直线尽可能地拟合图中的数据点。
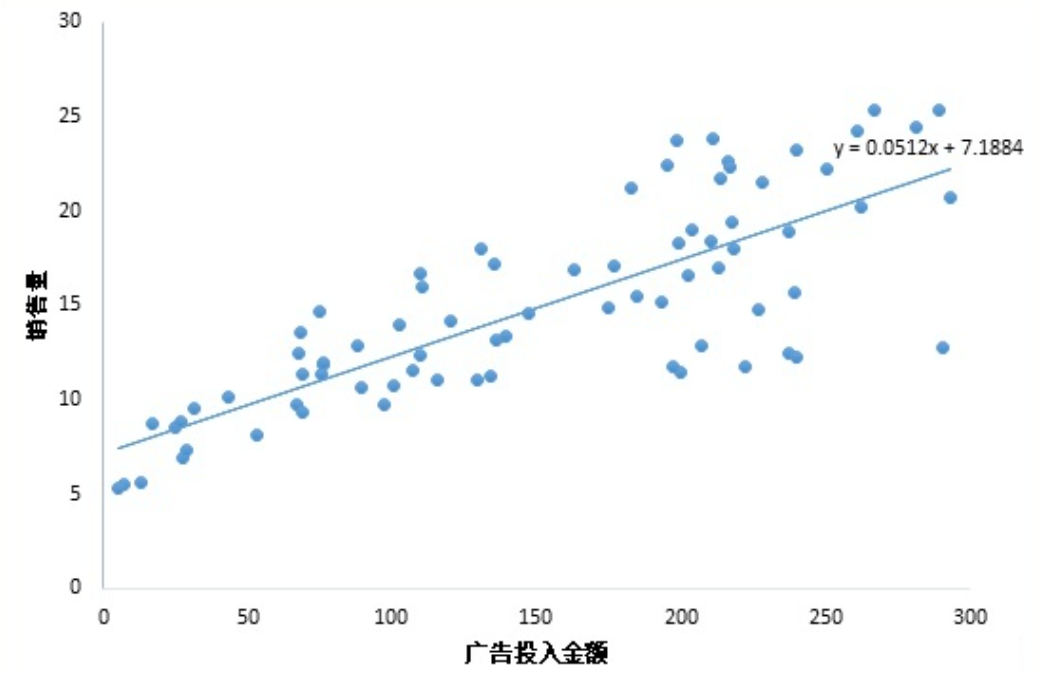
这里我们得到的拟合方程是y = 0.0512x + 7.1884,此时当我们获得一个新的广告投入金额后,我们就可以用这个方程预测出大概的销售量。
线性回归(Linear Regression)是一种用于建立和分析关于两个或多个变量之间线性关系的统计方法和机器学习算法。它被广泛应用于预测和建模任务,尤其是用于预测数值型输出(连续型变量)。
线性回归的基本思想是寻找自变量(输入特征)与因变量(输出目标)之间的线性关系,即一个线性方程,用来描述这些变量之间的关系。一般来说,线性回归模型的方程如下:


线性回归适用于以下情况:
- 希望理解和建模两个或多个变量之间的线性关系。
- 需要进行数值型输出的预测。
- 需要估计特征对目标变量的影响。
- 需要进行简单的模型解释和解释能力较强的建模。
线性回归是机器学习和统计学中最简单但也是最有用的工具之一,它为许多预测问题提供了一个坚实的基础。在实际应用中,线性回归通常有多种变体,如多元线性回归、岭回归、Lasso回归等,以适应不同问题的需求。
注意 :做线性回归,不要忘了前提假设是y和x呈线性关系,如果两者不是线性关系,就要选用其他的模型啦。
线性回归案例
#导入必要的库
import numpy as np
import pandas as pd
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# 加载波士顿房价数据集
boston = datasets.load_boston()
#data:这是一个NumPy数组,包含了数据集的特征值。每一行代表一个数据样本,每一列代表一个特征。
boston.data
array([[6.3200e-03, 1.8000e+01, 2.3100e+00, ..., 1.5300e+01, 3.9690e+02,
4.9800e+00],
[2.7310e-02, 0.0000e+00, 7.0700e+00, ..., 1.7800e+01, 3.9690e+02,
9.1400e+00],
[2.7290e-02, 0.0000e+00, 7.0700e+00, ..., 1.7800e+01, 3.9283e+02,
4.0300e+00],
...,
[6.0760e-02, 0.0000e+00, 1.1930e+01, ..., 2.1000e+01, 3.9690e+02,
5.6400e+00],
[1.0959e-01, 0.0000e+00, 1.1930e+01, ..., 2.1000e+01, 3.9345e+02,
6.4800e+00],
[4.7410e-02, 0.0000e+00, 1.1930e+01, ..., 2.1000e+01, 3.9690e+02,
7.8800e+00]])
#feature_names:这是一个字符串数组,包含了与data中的列对应的特征名称。
boston.feature_names
array(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',
'TAX', 'PTRATIO', 'B', 'LSTAT'], dtype='<U7')
#target:这是一个NumPy数组,包含了数据集的目标变量,也就是房价。
boston.target
array([24. , 21.6, 34.7, 33.4, 36.2, 28.7, 22.9, 27.1, 16.5, 18.9, 15. ,
18.9, 21.7, 20.4, 18.2, 19.9, 23.1, 17.5, 20.2, 18.2, 13.6, 19.6,
15.2, 14.5, 15.6, 13.9, 16.6, 14.8, 18.4, 21. , 12.7, 14.5, 13.2,
13.1, 13.5, 18.9, 20. , 21. , 24.7, 30.8, 34.9, 26.6, 25.3, 24.7,
21.2, 19.3, 20. , 16.6, 14.4, 19.4, 19.7, 20.5, 25. , 23.4, 18.9,
35.4, 24.7, 31.6, 23.3, 19.6, 18.7, 16. , 22.2, 25. , 33. , 23.5,
19.4, 22. , 17.4, 20.9, 24.2, 21.7, 22.8, 23.4, 24.1, 21.4, 20. ,
20.8, 21.2, 20.3, 28. , 23.9, 24.8, 22.9, 23.9, 26.6, 22.5, 22.2,
23.6, 28.7, 22.6, 22. , 22.9, 25. , 20.6, 28.4, 21.4, 38.7, 43.8,
33.2, 27.5, 26.5, 18.6, 19.3, 20.1, 19.5, 19.5, 20.4, 19.8, 19.4,
21.7, 22.8, 18.8, 18.7, 18.5, 18.3, 21.2, 19.2, 20.4, 19.3, 22. ,
20.3, 20.5, 17.3, 18.8, 21.4, 15.7, 16.2, 18. , 14.3, 19.2, 19.6,
23. , 18.4, 15.6, 18.1, 17.4, 17.1, 13.3, 17.8, 14. , 14.4, 13.4,
15.6, 11.8, 13.8, 15.6, 14.6, 17.8, 15.4, 21.5, 19.6, 15.3, 19.4,
17. , 15.6, 13.1, 41.3, 24.3, 23.3, 27. , 50. , 50. , 50. , 22.7,
25. , 50. , 23.8, 23.8, 22.3, 17.4, 19.1, 23.1, 23.6, 22.6, 29.4,
23.2, 24.6, 29.9, 37.2, 39.8, 36.2, 37.9, 32.5, 26.4, 29.6, 50. ,
32. , 29.8, 34.9, 37. , 30.5, 36.4, 31.1, 29.1, 50. , 33.3, 30.3,
34.6, 34.9, 32.9, 24.1, 42.3, 48.5, 50. , 22.6, 24.4, 22.5, 24.4,
20. , 21.7, 19.3, 22.4, 28.1, 23.7, 25. , 23.3, 28.7, 21.5, 23. ,
26.7, 21.7, 27.5, 30.1, 44.8, 50. , 37.6, 31.6, 46.7, 31.5, 24.3,
31.7, 41.7, 48.3, 29. , 24. , 25.1, 31.5, 23.7, 23.3, 22. , 20.1,
22.2, 23.7, 17.6, 18.5, 24.3, 20.5, 24.5, 26.2, 24.4, 24.8, 29.6,
42.8, 21.9, 20.9, 44. , 50. , 36. , 30.1, 33.8, 43.1, 48.8, 31. ,
36.5, 22.8, 30.7, 50. , 43.5, 20.7, 21.1, 25.2, 24.4, 35.2, 32.4,
32. , 33.2, 33.1, 29.1, 35.1, 45.4, 35.4, 46. , 50. , 32.2, 22. ,
20.1, 23.2, 22.3, 24.8, 28.5, 37.3, 27.9, 23.9, 21.7, 28.6, 27.1,
20.3, 22.5, 29. , 24.8, 22. , 26.4, 33.1, 36.1, 28.4, 33.4, 28.2,
22.8, 20.3, 16.1, 22.1, 19.4, 21.6, 23.8, 16.2, 17.8, 19.8, 23.1,
21. , 23.8, 23.1, 20.4, 18.5, 25. , 24.6, 23. , 22.2, 19.3, 22.6,
19.8, 17.1, 19.4, 22.2, 20.7, 21.1, 19.5, 18.5, 20.6, 19. , 18.7,
32.7, 16.5, 23.9, 31.2, 17.5, 17.2, 23.1, 24.5, 26.6, 22.9, 24.1,
18.6, 30.1, 18.2, 20.6, 17.8, 21.7, 22.7, 22.6, 25. , 19.9, 20.8,
16.8, 21.9, 27.5, 21.9, 23.1, 50. , 50. , 50. , 50. , 50. , 13.8,
13.8, 15. , 13.9, 13.3, 13.1, 10.2, 10.4, 10.9, 11.3, 12.3, 8.8,
7.2, 10.5, 7.4, 10.2, 11.5, 15.1, 23.2, 9.7, 13.8, 12.7, 13.1,
12.5, 8.5, 5. , 6.3, 5.6, 7.2, 12.1, 8.3, 8.5, 5. , 11.9,
27.9, 17.2, 27.5, 15. , 17.2, 17.9, 16.3, 7. , 7.2, 7.5, 10.4,
8.8, 8.4, 16.7, 14.2, 20.8, 13.4, 11.7, 8.3, 10.2, 10.9, 11. ,
9.5, 14.5, 14.1, 16.1, 14.3, 11.7, 13.4, 9.6, 8.7, 8.4, 12.8,
10.5, 17.1, 18.4, 15.4, 10.8, 11.8, 14.9, 12.6, 14.1, 13. , 13.4,
15.2, 16.1, 17.8, 14.9, 14.1, 12.7, 13.5, 14.9, 20. , 16.4, 17.7,
19.5, 20.2, 21.4, 19.9, 19. , 19.1, 19.1, 20.1, 19.9, 19.6, 23.2,
29.8, 13.8, 13.3, 16.7, 12. , 14.6, 21.4, 23. , 23.7, 25. , 21.8,
20.6, 21.2, 19.1, 20.6, 15.2, 7. , 8.1, 13.6, 20.1, 21.8, 24.5,
23.1, 19.7, 18.3, 21.2, 17.5, 16.8, 22.4, 20.6, 23.9, 22. , 11.9])
# 转换数据为DataFrame
boston_df = pd.DataFrame(boston.data, columns=boston.feature_names)
boston_df.head()
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0.0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1.0 | 296.0 | 15.3 | 396.90 | 4.98 |
| 1 | 0.02731 | 0.0 | 7.07 | 0.0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2.0 | 242.0 | 17.8 | 396.90 | 9.14 |
| 2 | 0.02729 | 0.0 | 7.07 | 0.0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2.0 | 242.0 | 17.8 | 392.83 | 4.03 |
| 3 | 0.03237 | 0.0 | 2.18 | 0.0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3.0 | 222.0 | 18.7 | 394.63 | 2.94 |
| 4 | 0.06905 | 0.0 | 2.18 | 0.0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3.0 | 222.0 | 18.7 | 396.90 | 5.33 |
CRIM:各城镇的人均犯罪率。
ZN:占地面积超过 25,000 平方英尺的住宅用地的比例。
INDUS:城镇非零售商业用地的比例。
CHAS:查尔斯河虚拟变量(如果一条街道临近查尔斯河,取值为1;否则,取值为0)。
NOX:一氧化氮浓度(每百万份)。
RM:住宅平均房间数。
AGE:1940 年之前建造的自住房屋的比例。
DIS:到就业中心的加权距离。
RAD:到径向公路的可达性指数。
TAX:房产税率。
PTRATIO:城镇的师生比例。
B:1000(Bk - 0.63)^2,其中Bk是城镇中黑人的比例。
LSTAT:较低社会地位人口的百分比。
MEDV:自住房的中位数房价,这是该数据集的目标变量。
boston_df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 506 entries, 0 to 505
Data columns (total 13 columns):
CRIM 506 non-null float64
ZN 506 non-null float64
INDUS 506 non-null float64
CHAS 506 non-null float64
NOX 506 non-null float64
RM 506 non-null float64
AGE 506 non-null float64
DIS 506 non-null float64
RAD 506 non-null float64
TAX 506 non-null float64
PTRATIO 506 non-null float64
B 506 non-null float64
LSTAT 506 non-null float64
dtypes: float64(13)
memory usage: 51.5 KB
# 将目标(房价)添加到DataFrame
boston_df['PRICE'] = boston.target
boston.target
array([24. , 21.6, 34.7, 33.4, 36.2, 28.7, 22.9, 27.1, 16.5, 18.9, 15. ,
18.9, 21.7, 20.4, 18.2, 19.9, 23.1, 17.5, 20.2, 18.2, 13.6, 19.6,
15.2, 14.5, 15.6, 13.9, 16.6, 14.8, 18.4, 21. , 12.7, 14.5, 13.2,
13.1, 13.5, 18.9, 20. , 21. , 24.7, 30.8, 34.9, 26.6, 25.3, 24.7,
21.2, 19.3, 20. , 16.6, 14.4, 19.4, 19.7, 20.5, 25. , 23.4, 18.9,
35.4, 24.7, 31.6, 23.3, 19.6, 18.7, 16. , 22.2, 25. , 33. , 23.5,
19.4, 22. , 17.4, 20.9, 24.2, 21.7, 22.8, 23.4, 24.1, 21.4, 20. ,
20.8, 21.2, 20.3, 28. , 23.9, 24.8, 22.9, 23.9, 26.6, 22.5, 22.2,
23.6, 28.7, 22.6, 22. , 22.9, 25. , 20.6, 28.4, 21.4, 38.7, 43.8,
33.2, 27.5, 26.5, 18.6, 19.3, 20.1, 19.5, 19.5, 20.4, 19.8, 19.4,
21.7, 22.8, 18.8, 18.7, 18.5, 18.3, 21.2, 19.2, 20.4, 19.3, 22. ,
20.3, 20.5, 17.3, 18.8, 21.4, 15.7, 16.2, 18. , 14.3, 19.2, 19.6,
23. , 18.4, 15.6, 18.1, 17.4, 17.1, 13.3, 17.8, 14. , 14.4, 13.4,
15.6, 11.8, 13.8, 15.6, 14.6, 17.8, 15.4, 21.5, 19.6, 15.3, 19.4,
17. , 15.6, 13.1, 41.3, 24.3, 23.3, 27. , 50. , 50. , 50. , 22.7,
25. , 50. , 23.8, 23.8, 22.3, 17.4, 19.1, 23.1, 23.6, 22.6, 29.4,
23.2, 24.6, 29.9, 37.2, 39.8, 36.2, 37.9, 32.5, 26.4, 29.6, 50. ,
32. , 29.8, 34.9, 37. , 30.5, 36.4, 31.1, 29.1, 50. , 33.3, 30.3,
34.6, 34.9, 32.9, 24.1, 42.3, 48.5, 50. , 22.6, 24.4, 22.5, 24.4,
20. , 21.7, 19.3, 22.4, 28.1, 23.7, 25. , 23.3, 28.7, 21.5, 23. ,
26.7, 21.7, 27.5, 30.1, 44.8, 50. , 37.6, 31.6, 46.7, 31.5, 24.3,
31.7, 41.7, 48.3, 29. , 24. , 25.1, 31.5, 23.7, 23.3, 22. , 20.1,
22.2, 23.7, 17.6, 18.5, 24.3, 20.5, 24.5, 26.2, 24.4, 24.8, 29.6,
42.8, 21.9, 20.9, 44. , 50. , 36. , 30.1, 33.8, 43.1, 48.8, 31. ,
36.5, 22.8, 30.7, 50. , 43.5, 20.7, 21.1, 25.2, 24.4, 35.2, 32.4,
32. , 33.2, 33.1, 29.1, 35.1, 45.4, 35.4, 46. , 50. , 32.2, 22. ,
20.1, 23.2, 22.3, 24.8, 28.5, 37.3, 27.9, 23.9, 21.7, 28.6, 27.1,
20.3, 22.5, 29. , 24.8, 22. , 26.4, 33.1, 36.1, 28.4, 33.4, 28.2,
22.8, 20.3, 16.1, 22.1, 19.4, 21.6, 23.8, 16.2, 17.8, 19.8, 23.1,
21. , 23.8, 23.1, 20.4, 18.5, 25. , 24.6, 23. , 22.2, 19.3, 22.6,
19.8, 17.1, 19.4, 22.2, 20.7, 21.1, 19.5, 18.5, 20.6, 19. , 18.7,
32.7, 16.5, 23.9, 31.2, 17.5, 17.2, 23.1, 24.5, 26.6, 22.9, 24.1,
18.6, 30.1, 18.2, 20.6, 17.8, 21.7, 22.7, 22.6, 25. , 19.9, 20.8,
16.8, 21.9, 27.5, 21.9, 23.1, 50. , 50. , 50. , 50. , 50. , 13.8,
13.8, 15. , 13.9, 13.3, 13.1, 10.2, 10.4, 10.9, 11.3, 12.3, 8.8,
7.2, 10.5, 7.4, 10.2, 11.5, 15.1, 23.2, 9.7, 13.8, 12.7, 13.1,
12.5, 8.5, 5. , 6.3, 5.6, 7.2, 12.1, 8.3, 8.5, 5. , 11.9,
27.9, 17.2, 27.5, 15. , 17.2, 17.9, 16.3, 7. , 7.2, 7.5, 10.4,
8.8, 8.4, 16.7, 14.2, 20.8, 13.4, 11.7, 8.3, 10.2, 10.9, 11. ,
9.5, 14.5, 14.1, 16.1, 14.3, 11.7, 13.4, 9.6, 8.7, 8.4, 12.8,
10.5, 17.1, 18.4, 15.4, 10.8, 11.8, 14.9, 12.6, 14.1, 13. , 13.4,
15.2, 16.1, 17.8, 14.9, 14.1, 12.7, 13.5, 14.9, 20. , 16.4, 17.7,
19.5, 20.2, 21.4, 19.9, 19. , 19.1, 19.1, 20.1, 19.9, 19.6, 23.2,
29.8, 13.8, 13.3, 16.7, 12. , 14.6, 21.4, 23. , 23.7, 25. , 21.8,
20.6, 21.2, 19.1, 20.6, 15.2, 7. , 8.1, 13.6, 20.1, 21.8, 24.5,
23.1, 19.7, 18.3, 21.2, 17.5, 16.8, 22.4, 20.6, 23.9, 22. , 11.9])
# 划分特征和目标变量
X = boston_df.drop('PRICE', axis=1)
y = boston_df['PRICE']
# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=100)
X_train
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 379 | 17.86670 | 0.0 | 18.10 | 0.0 | 0.6710 | 6.223 | 100.0 | 1.3861 | 24.0 | 666.0 | 20.2 | 393.74 | 21.78 |
| 311 | 0.79041 | 0.0 | 9.90 | 0.0 | 0.5440 | 6.122 | 52.8 | 2.6403 | 4.0 | 304.0 | 18.4 | 396.90 | 5.98 |
| 157 | 1.22358 | 0.0 | 19.58 | 0.0 | 0.6050 | 6.943 | 97.4 | 1.8773 | 5.0 | 403.0 | 14.7 | 363.43 | 4.59 |
| 244 | 0.20608 | 22.0 | 5.86 | 0.0 | 0.4310 | 5.593 | 76.5 | 7.9549 | 7.0 | 330.0 | 19.1 | 372.49 | 12.50 |
| 56 | 0.02055 | 85.0 | 0.74 | 0.0 | 0.4100 | 6.383 | 35.7 | 9.1876 | 2.0 | 313.0 | 17.3 | 396.90 | 5.77 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 343 | 0.02543 | 55.0 | 3.78 | 0.0 | 0.4840 | 6.696 | 56.4 | 5.7321 | 5.0 | 370.0 | 17.6 | 396.90 | 7.18 |
| 359 | 4.26131 | 0.0 | 18.10 | 0.0 | 0.7700 | 6.112 | 81.3 | 2.5091 | 24.0 | 666.0 | 20.2 | 390.74 | 12.67 |
| 323 | 0.28392 | 0.0 | 7.38 | 0.0 | 0.4930 | 5.708 | 74.3 | 4.7211 | 5.0 | 287.0 | 19.6 | 391.13 | 11.74 |
| 280 | 0.03578 | 20.0 | 3.33 | 0.0 | 0.4429 | 7.820 | 64.5 | 4.6947 | 5.0 | 216.0 | 14.9 | 387.31 | 3.76 |
| 8 | 0.21124 | 12.5 | 7.87 | 0.0 | 0.5240 | 5.631 | 100.0 | 6.0821 | 5.0 | 311.0 | 15.2 | 386.63 | 29.93 |
404 rows × 13 columns
X_test
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 198 | 0.03768 | 80.0 | 1.52 | 0.0 | 0.404 | 7.274 | 38.3 | 7.3090 | 2.0 | 329.0 | 12.6 | 392.20 | 6.62 |
| 229 | 0.44178 | 0.0 | 6.20 | 0.0 | 0.504 | 6.552 | 21.4 | 3.3751 | 8.0 | 307.0 | 17.4 | 380.34 | 3.76 |
| 502 | 0.04527 | 0.0 | 11.93 | 0.0 | 0.573 | 6.120 | 76.7 | 2.2875 | 1.0 | 273.0 | 21.0 | 396.90 | 9.08 |
| 31 | 1.35472 | 0.0 | 8.14 | 0.0 | 0.538 | 6.072 | 100.0 | 4.1750 | 4.0 | 307.0 | 21.0 | 376.73 | 13.04 |
| 315 | 0.25356 | 0.0 | 9.90 | 0.0 | 0.544 | 5.705 | 77.7 | 3.9450 | 4.0 | 304.0 | 18.4 | 396.42 | 11.50 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 166 | 2.01019 | 0.0 | 19.58 | 0.0 | 0.605 | 7.929 | 96.2 | 2.0459 | 5.0 | 403.0 | 14.7 | 369.30 | 3.70 |
| 401 | 14.23620 | 0.0 | 18.10 | 0.0 | 0.693 | 6.343 | 100.0 | 1.5741 | 24.0 | 666.0 | 20.2 | 396.90 | 20.32 |
| 368 | 4.89822 | 0.0 | 18.10 | 0.0 | 0.631 | 4.970 | 100.0 | 1.3325 | 24.0 | 666.0 | 20.2 | 375.52 | 3.26 |
| 140 | 0.29090 | 0.0 | 21.89 | 0.0 | 0.624 | 6.174 | 93.6 | 1.6119 | 4.0 | 437.0 | 21.2 | 388.08 | 24.16 |
| 428 | 7.36711 | 0.0 | 18.10 | 0.0 | 0.679 | 6.193 | 78.1 | 1.9356 | 24.0 | 666.0 | 20.2 | 96.73 | 21.52 |
102 rows × 13 columns
y_train
379 10.2
311 22.1
157 41.3
244 17.6
56 24.7
...
343 23.9
359 22.6
323 18.5
280 45.4
8 16.5
Name: PRICE, Length: 404, dtype: float64
y_test
198 34.6
229 31.5
502 20.6
31 14.5
315 16.2
...
166 50.0
401 7.2
368 50.0
140 14.0
428 11.0
Name: PRICE, Length: 102, dtype: float64
# 创建线性回归模型
model = LinearRegression()
# 拟合模型
model.fit(X_train, y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
# 预测房价
y_pred = model.predict(X_test)
y_pred
array([34.4081095 , 31.18524626, 22.31286141, 17.88613877, 20.43572131,
26.14444413, 26.21920244, 23.57978445, 22.41577853, 19.51182817,
26.86691495, 17.20411302, 20.68511041, 15.67921778, 41.69912781,
20.2946735 , 28.99258631, 19.06413492, 32.48035595, 41.13627224,
34.64732462, 16.38997909, 20.42215729, 18.05324255, 13.38743087,
12.64800748, 27.45930237, 20.30199107, 18.78954741, 20.24950994,
15.60161419, 24.38040555, 38.95651978, 24.7184131 , 31.26791961,
28.26279775, 15.84707127, 14.76661568, 16.79024244, 23.23674899,
22.85417065, 23.48976177, 14.16818173, 21.42613087, 32.38362329,
26.7881669 , 19.37574824, 15.27894103, 17.21175121, 12.91591919,
21.84063224, 20.25050371, 23.65622638, 23.9608324 , 11.94749102,
14.49718052, 24.69872363, 34.18169066, 10.30437821, 21.04686616,
17.96204214, 19.76593459, 17.45231513, 29.982971 , 20.73183476,
25.24657823, 15.81416285, 24.96705225, 22.1298931 , 20.77593563,
18.69600904, 24.2201495 , 4.37889874, 15.95687399, 28.03130587,
9.28438308, 24.76810967, 35.14238234, 11.61172029, 27.04175401,
34.84290485, 40.44603313, 13.93219791, 15.95544402, 19.26007763,
12.76037799, 20.90536105, 23.85659356, 13.17899179, 14.76828889,
32.31355353, 22.93635318, 24.63095357, 23.51981407, 19.34136578,
22.83582245, 21.72263765, 36.18508621, 18.01097012, 23.18226475,
13.77270991, 14.43864146])
# 创建一个新的DataFrame,将实际值、预测值和特征合并在一起
results_df = X_test.copy()
results_df['Actual_Price'] = y_test
results_df['Predicted_Price'] = y_pred
results_df.head(10)
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | Actual_Price | Predicted_Price | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 198 | 0.03768 | 80.0 | 1.52 | 0.0 | 0.404 | 7.274 | 38.3 | 7.3090 | 2.0 | 329.0 | 12.6 | 392.20 | 6.62 | 34.6 | 34.408110 |
| 229 | 0.44178 | 0.0 | 6.20 | 0.0 | 0.504 | 6.552 | 21.4 | 3.3751 | 8.0 | 307.0 | 17.4 | 380.34 | 3.76 | 31.5 | 31.185246 |
| 502 | 0.04527 | 0.0 | 11.93 | 0.0 | 0.573 | 6.120 | 76.7 | 2.2875 | 1.0 | 273.0 | 21.0 | 396.90 | 9.08 | 20.6 | 22.312861 |
| 31 | 1.35472 | 0.0 | 8.14 | 0.0 | 0.538 | 6.072 | 100.0 | 4.1750 | 4.0 | 307.0 | 21.0 | 376.73 | 13.04 | 14.5 | 17.886139 |
| 315 | 0.25356 | 0.0 | 9.90 | 0.0 | 0.544 | 5.705 | 77.7 | 3.9450 | 4.0 | 304.0 | 18.4 | 396.42 | 11.50 | 16.2 | 20.435721 |
| 169 | 2.44953 | 0.0 | 19.58 | 0.0 | 0.605 | 6.402 | 95.2 | 2.2625 | 5.0 | 403.0 | 14.7 | 330.04 | 11.32 | 22.3 | 26.144444 |
| 111 | 0.10084 | 0.0 | 10.01 | 0.0 | 0.547 | 6.715 | 81.6 | 2.6775 | 6.0 | 432.0 | 17.8 | 395.59 | 10.16 | 22.8 | 26.219202 |
| 206 | 0.22969 | 0.0 | 10.59 | 0.0 | 0.489 | 6.326 | 52.5 | 4.3549 | 4.0 | 277.0 | 18.6 | 394.87 | 10.97 | 24.4 | 23.579784 |
| 108 | 0.12802 | 0.0 | 8.56 | 0.0 | 0.520 | 6.474 | 97.1 | 2.4329 | 5.0 | 384.0 | 20.9 | 395.24 | 12.27 | 19.8 | 22.415779 |
| 420 | 11.08740 | 0.0 | 18.10 | 0.0 | 0.718 | 6.411 | 100.0 | 1.8589 | 24.0 | 666.0 | 20.2 | 318.75 | 15.02 | 16.7 | 19.511828 |
# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
mse
23.616994100563634
# 计算R-squared(决定系数)
r2 = r2_score(y_test, y_pred)
r2
0.7555033086871304
线性回归的评价指标
- 均方误差(Mean Squared Error,MSE):MSE是最常用的线性回归模型评价指标之一。它计算了模型的预测值与实际观测值之间的平方差的平均值。MSE越小,模型的拟合能力越好。
公式:MSE = Σ(yi - ŷi)² / n,其中 yi 表示实际观测值,ŷi 表示模型的预测值,n 表示样本数量。
- 均方根误差(Root Mean Squared Error,RMSE):RMSE是MSE的平方根,它在与实际数据单位相同的度量下提供了误差的平均大小。RMSE也越小越好。
公式:RMSE = √(Σ(yi - ŷi)² / n)
- 平均绝对误差(Mean Absolute Error,MAE):MAE计算了模型的预测值与实际观测值之间的绝对差的平均值。MAE越小,表示模型对数据的拟合越好。
公式:MAE = Σ|yi - ŷi| / n
- 决定系数(Coefficient of Determination,R-squared,R²):R²度量了线性回归模型对数据的拟合程度。它的取值范围在0到1之间,越接近1表示模型拟合得越好。
公式:R² = 1 - (Σ(yi - ŷi)² / Σ(yi - ȳ)²),其中 yi 表示实际观测值,ŷi 表示模型的预测值,ȳ 表示实际观测值的均值。