题目
给定长度为 N 的数列 A,然后输入 M 行操作指令。
第一类指令形如 C l r d,表示把数列中第 l∼r 个数都加 d。
第二类指令形如 Q x,表示询问数列中第 x 个数的值。
对于每个询问,输出一个整数表示答案。
输入格式
第一行包含两个整数 N 和 M。
第二行包含 N 个整数 A[ i ]。
接下来 M 行表示 M 条指令,每条指令的格式如题目描述所示。
输出格式
对于每个询问,输出一个整数表示答案。
每个答案占一行。
数据范围
1 ≤ N,M ≤ 10^5
|d| ≤ 10000
|A[i]| ≤ 10^9
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
Q 4
Q 1
Q 2
C 1 6 3
Q 2
输出样例:
4
1
2
5思路

我们可以使用树状数组维护差分数组,这样更改与查询的时间复杂度均为O(log(n))。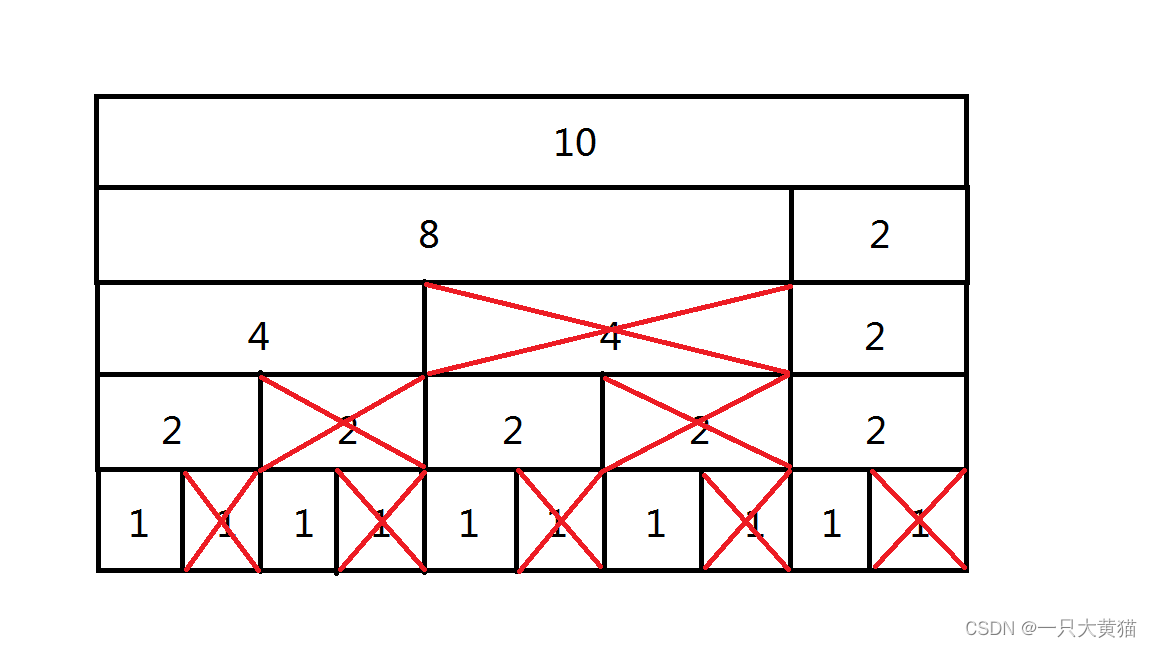
得到树状数组
| 1 | 2 | 1 | 4 | 1 | 2 | 1 | 8 | 1 | 2 |
若更新某一区间的值,需要更改[l,r+1)的值,但是在差分数组中只需更改 l 与 r + 1的值。
若要取某个点的值,只需求一下差分数组的前缀和,得到的值就为该点的实际值。
代码
#include<bits/stdc++.h>
#define int long long
#define N 100010
using namespace std;
int n,m;
int a[N];
int tr[N];
int lowbit(int x)
{
return x & -x;
}
void add(int x,int c)
{
for(int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
int sum(int x)
{
int res = 0;
while(x)
{
res += tr[x];
x -= lowbit(x);
}
return res;
}
int32_t main()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> a[i];
for(int i = 1; i <= n; i ++) add(i,a[i] - a[i - 1]);// 使用树状数组维护差分数组
while(m --)
{
string op;
int l,r,d;
cin >> op >> l;
if(op == "C")
{
cin >> r >> d;
add(l,d),add(r + 1, -d);// 在差分数组的[l ~ r + 1)之间的数全部加d
}
else
{
cout << sum(l) << endl;
}
}
return 0;
}