本专栏内容为:C++学习专栏,分为初阶和进阶两部分。 通过本专栏的深入学习,你可以了解并掌握C++。
💓博主csdn个人主页:小小unicorn
⏩专栏分类:C++
🚚代码仓库:小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识
C++初阶(九)
- priority_queue的使用
- priority_queue的介绍
- priority_queue的定义方式
- priority_queue的介绍
- priority_queue各个接口使用
- priority_queue的模拟实现
- 堆的向上调整法
- 堆的向下调整法
- 建堆时间复杂度:
- priority_queue的模拟实现
priority_queue的使用
priority_queue的介绍
优先级队列默认使用vector作为其底层存储数据的容器,在vector上又使用了堆算法将vector中的元素构造成堆的结构,因此priority_queue就是堆,所有需要用到堆的位置,都可以考虑使用priority_queue。
注意: 默认情况下priority_queue是大堆
priority_queue的定义方式
priority_queue的介绍
方式一: 使用vector作为底层容器,内部构造大堆结构。
priority_queue<int, vector<int>, less<int>> q1;
方式二: 使用vector作为底层容器,内部构造小堆结构。
priority_queue<int, vector<int>, greater<int>> q2;
方式三: 不指定底层容器和内部需要构造的堆结构。
priority_queue<int> q;
注意: 此时默认使用vector作为底层容器,内部默认构造大堆结构。
priority_queue各个接口使用
priority_queue的各个成员函数及其功能如下:
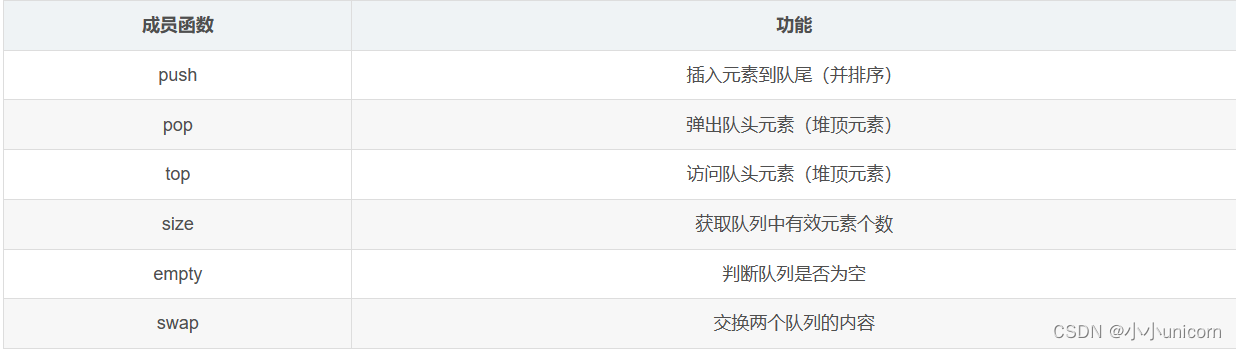
使用示例:
#include <iostream>
#include <functional>
#include <queue>
using namespace std;
int main()
{
priority_queue<int> q;
q.push(3);
q.push(6);
q.push(0);
q.push(2);
q.push(9);
q.push(8);
q.push(1);
while (!q.empty())
{
cout << q.top() << " ";
q.pop();
}
cout << endl; //9 8 6 3 2 1 0
return 0;
}
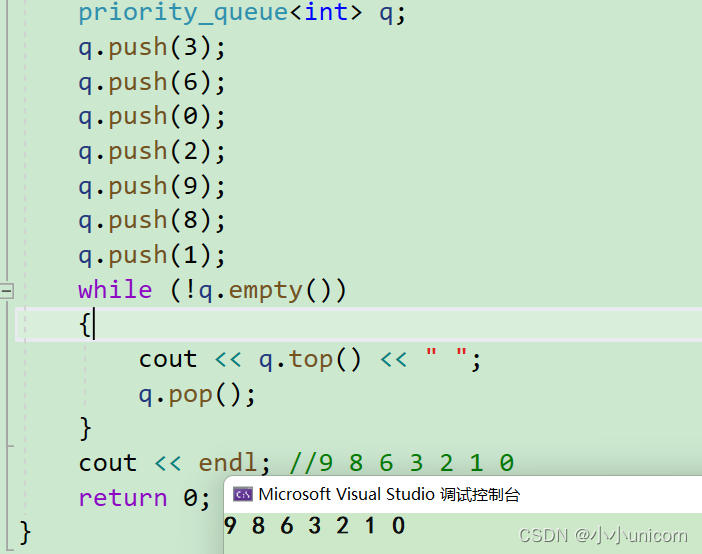
priority_queue的模拟实现
priority_queue的底层实际上就是堆结构,实现priority_queue之前,我们先认识两个重要的堆算法。(下面这两种算法我们均以大堆为例)
堆的向上调整法
当我们在一个堆的末尾插入一个数据后,需要对堆进行调整,使其仍然是一个堆,这时需要用到堆的向上调整算法。
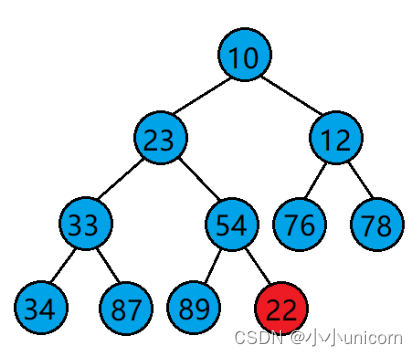
向上调整算法的基本思想(以建小堆为例):
1.将目标结点与其父结点比较。
2.若目标结点的值比其父结点的值小,则交换目标结点与其父结点的位置,并将原目标结点的父结点当作新的目标结点继续进行向上调整。若目标结点的值比其父结点的值大,则停止向上调整,此时该树已经是小堆了。
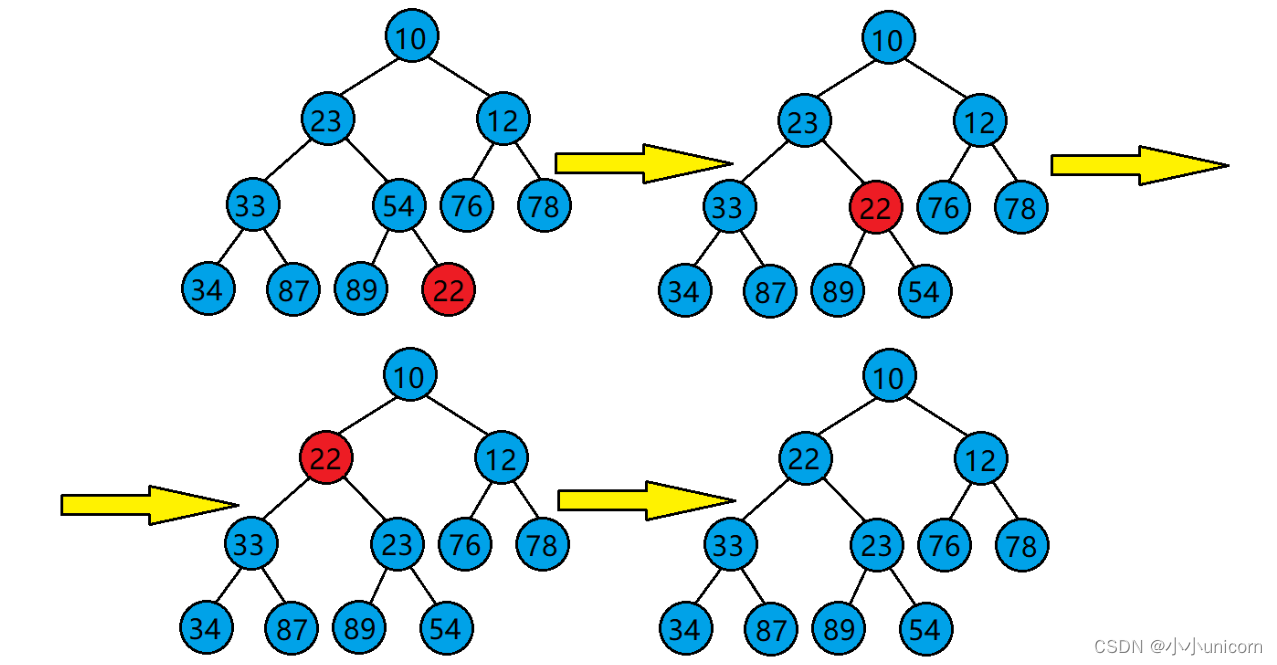
代码如下:
//交换函数
void Swap(HPDataType* x, HPDataType* y)
{
HPDataType tmp = *x;
*x = *y;
*y = tmp;
}
//堆的向上调整(小堆)
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)//调整到根结点的位置截止
{
if (a[child] < a[parent])//孩子结点的值小于父结点的值
{
//将父结点与孩子结点交换
Swap(&a[child], &a[parent]);
//继续向上进行调整
child = parent;
parent = (child - 1) / 2;
}
else//已成堆
{
break;
}
}
}
堆的向下调整法
现在我们给出一个数组,逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。
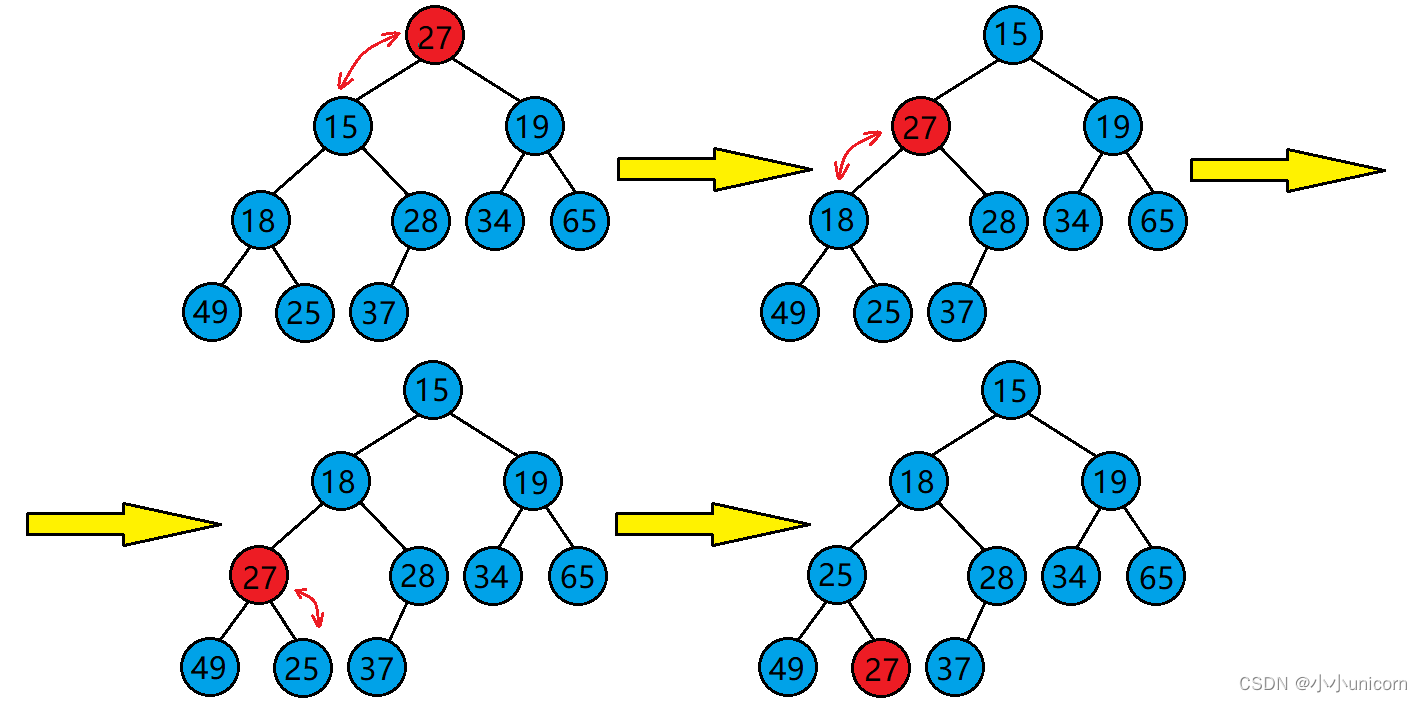
但是:向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
1.若想将其调整为小堆,那么根结点的左右子树必须都为小堆。
2.若想将其调整为大堆,那么根结点的左右子树必须都为大堆。
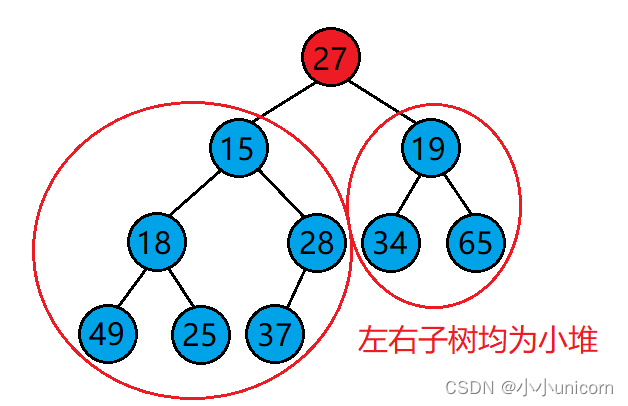
向下调整算法的基本思想(以建小堆为例):
1.从根结点处开始,选出左右孩子中值较小的孩子。
2.让小的孩子与其父亲进行比较。
若小的孩子比父亲还小,则该孩子与其父亲的位置进行交换。并将原来小的孩子的位置当成父亲继续向下进行调整,直到调整到叶子结点为止。
若小的孩子比父亲大,则不需处理了,调整完成,整个树已经是小堆了。
代码如下:
//交换函数
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
//堆的向下调整(小堆)
void AdjustDown(int* a, int n, int parent)
{
//child记录左右孩子中值较小的孩子的下标
int child = 2 * parent + 1;//先默认其左孩子的值较小
while (child < n)
{
if (child + 1 < n&&a[child + 1] < a[child])//右孩子存在并且右孩子比左孩子还小
{
child++;//较小的孩子改为右孩子
}
if (a[child] < a[parent])//左右孩子中较小孩子的值比父结点还小
{
//将父结点与较小的子结点交换
Swap(&a[child], &a[parent]);
//继续向下进行调整
parent = child;
child = 2 * parent + 1;
}
else//已成堆
{
break;
}
}
}
使用堆的向下调整算法,最坏的情况下(即一直需要交换结点),需要循环的次数为:h - 1次(h为树的高度)。而h = log2(N+1)(N为树的总结点数)。所以堆的向下调整算法的时间复杂度为:O(logN) 。
上面说到,使用堆的向下调整算法需要满足其根结点的左右子树均为大堆或是小堆才行,那么如何才能将一个任意树调整为堆,我们只需要从倒数第一个非叶子结点开始,从后往前,按下标,依次作为根去向下调整即可。
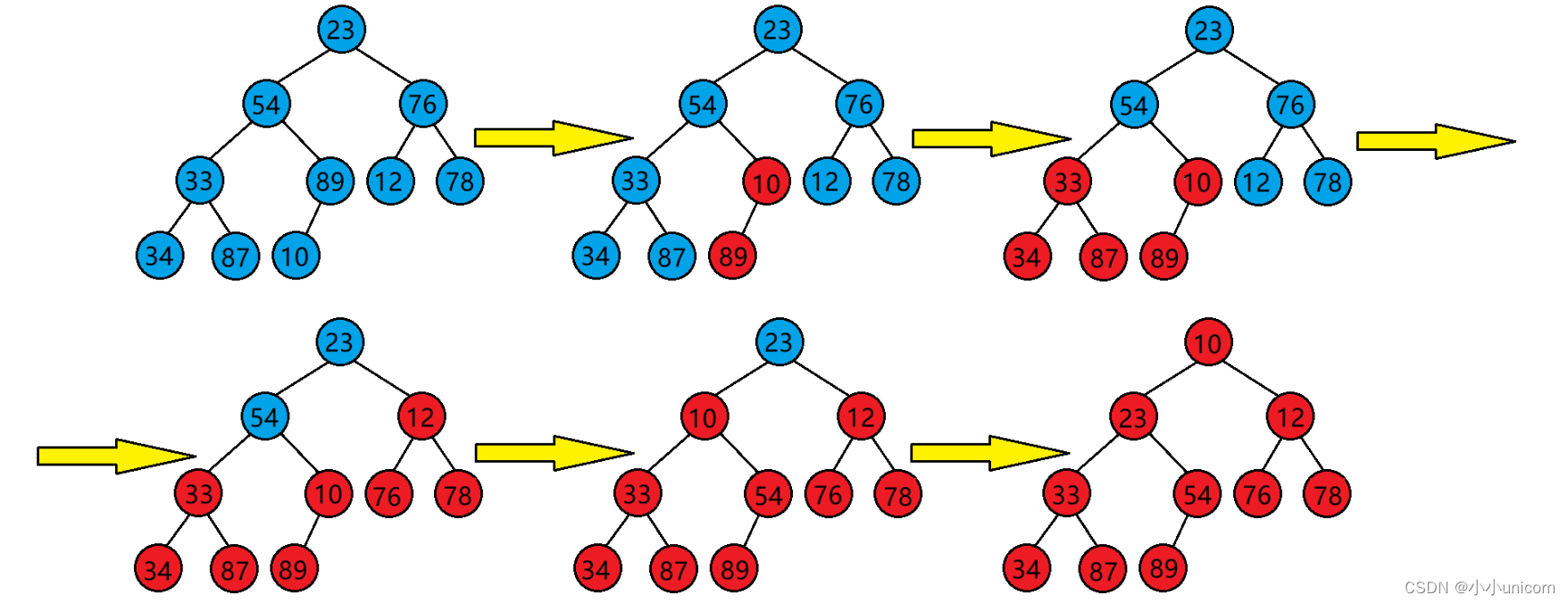
代码如下:
//建堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(php->a, php->size, i);
}
建堆时间复杂度:
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值,多几个节点不影响最终结果):
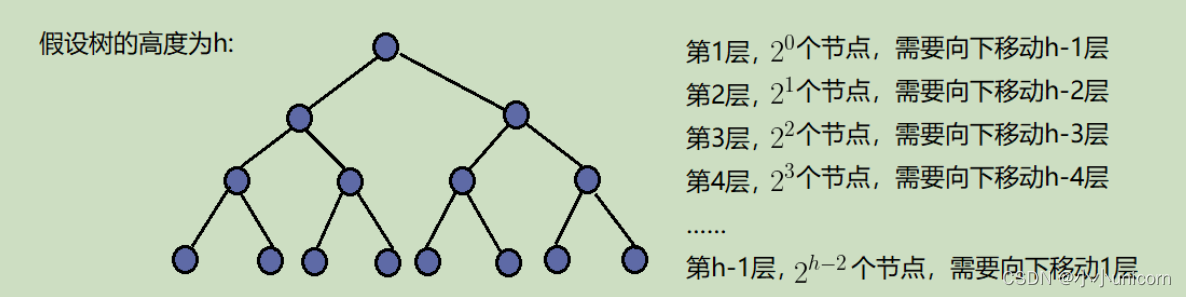
利用错位相减法进行计算:
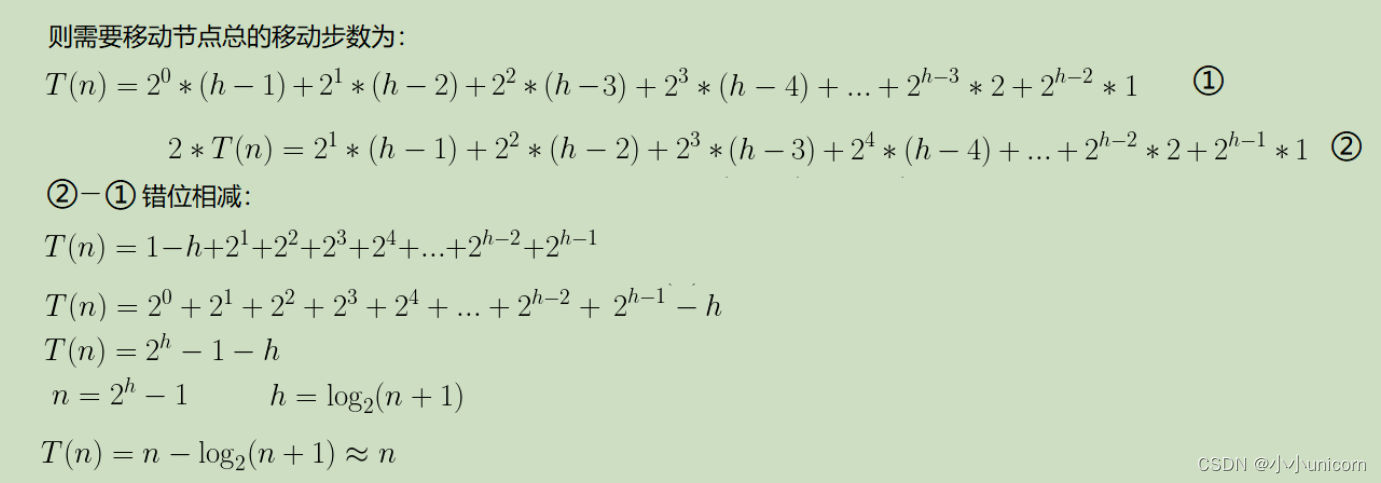
因此:建堆的时间复杂度为O(N)。
总结:
堆的向下调整算法的时间复杂度:T(n)=O(logN)。
建堆的时间复杂度:T(n)=O(N)。
priority_queue的模拟实现
只要知道了堆的向上调整算法和堆的向下调整算法,priority_queue的模拟实现就没什么困难了。
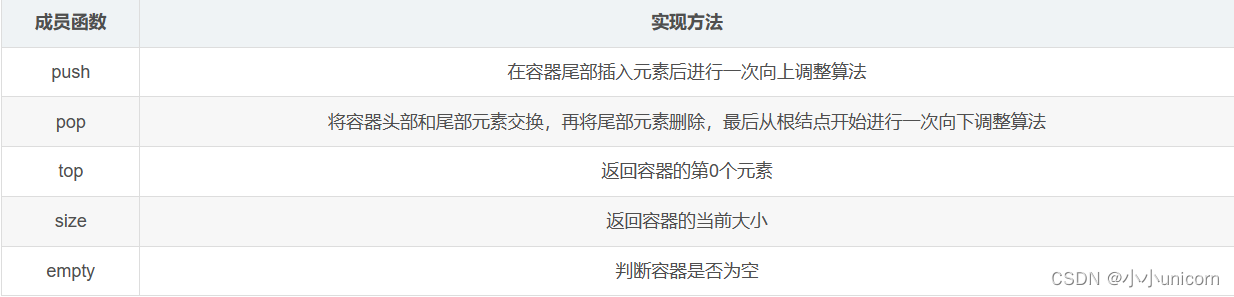
priority_queue的模拟实现代码:
namespace NIC //防止命名冲突
{
//比较方式(使内部结构为大堆)
template<class T>
struct less
{
bool operator()(const T& x, const T& y)
{
return x < y;
}
};
//比较方式(使内部结构为小堆)
template<class T>
struct greater
{
bool operator()(const T& x, const T& y)
{
return x > y;
}
};
//优先级队列的模拟实现
template<class T, class Container = vector<T>, class Compare = less<T>>
class priority_queue
{
public:
//堆的向上调整
void AdjustUp(int child)
{
int parent = (child - 1) / 2; //通过child计算parent的下标
while (child > 0)//调整到根结点的位置截止
{
if (_comp(_con[parent], _con[child]))//通过所给比较方式确定是否需要交换结点位置
{
//将父结点与孩子结点交换
swap(_con[child], _con[parent]);
//继续向上进行调整
child = parent;
parent = (child - 1) / 2;
}
else//已成堆
{
break;
}
}
}
//插入元素到队尾(并排序)
void push(const T& x)
{
_con.push_back(x);
AdjustUp(_con.size() - 1); //将最后一个元素进行一次向上调整
}
//堆的向下调整
void AdjustDown(int n, int parent)
{
int child = 2 * parent + 1;
while (child < n)
{
if (child + 1 < n && _comp(_con[child], _con[child + 1]))
{
child++;
}
if (_comp(_con[parent], _con[child]))//通过所给比较方式确定是否需要交换结点位置
{
//将父结点与孩子结点交换
swap(_con[child], _con[parent]);
//继续向下进行调整
parent = child;
child = 2 * parent + 1;
}
else//已成堆
{
break;
}
}
}
//弹出队头元素(堆顶元素)
void pop()
{
swap(_con[0], _con[_con.size() - 1]);
_con.pop_back();
AdjustDown(_con.size(), 0); //将第0个元素进行一次向下调整
}
//访问队头元素(堆顶元素)
T& top()
{
return _con[0];
}
const T& top() const
{
return _con[0];
}
//获取队列中有效元素个数
size_t size() const
{
return _con.size();
}
//判断队列是否为空
bool empty() const
{
return _con.empty();
}
private:
Container _con; //底层容器
Compare _comp; //比较方式
};
}
测试一下: