找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：
- 只使用数字1到9
- 每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。示例 3:
输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
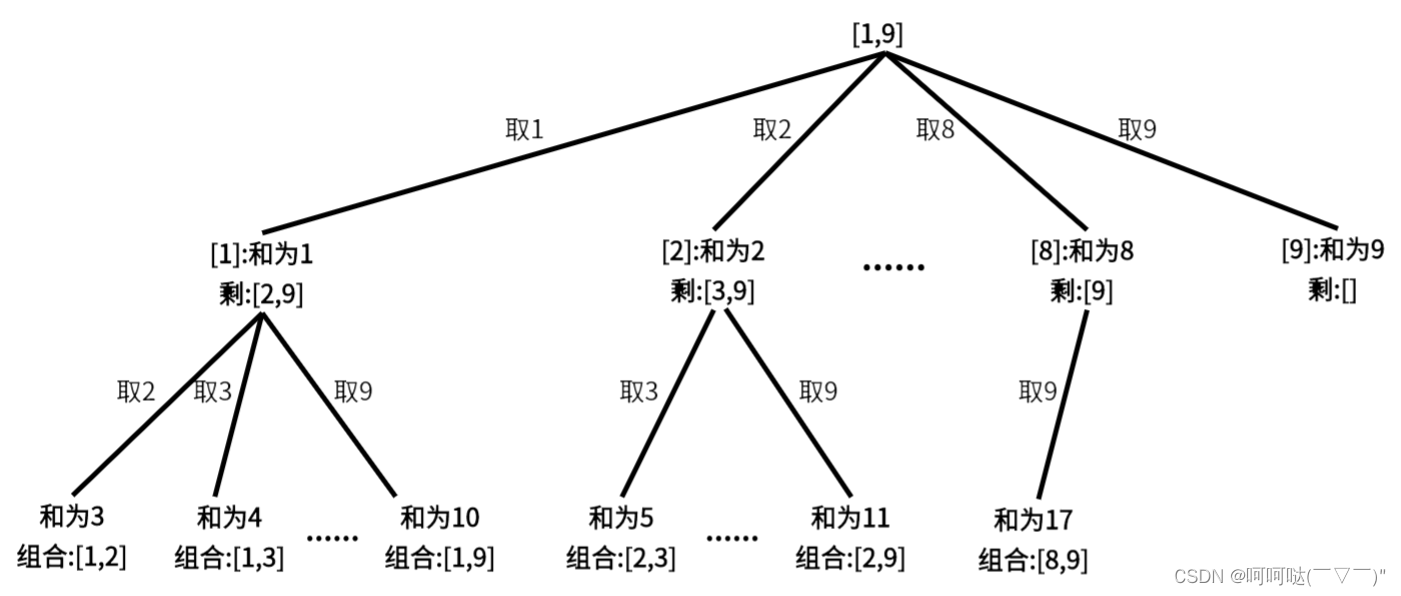
在[1,9]范围内使用4个不同的数字，我们可以得到的最小和是1+2+3+4 = 10，因为10 > 1，没有有效的组合。组合问题：给定一个 1~9 的组合，求和为 n ，个数为 k 的所有组合
【思路分析】可以通过回溯算法求解组合问题：元素不同的顺序是一样的组合，不能取重复的元素
回溯算法的实现过程，包括建立树形结构，遍历集合，剪枝等操作
- 通过树形结构来搜索符合要求的组合，k控制着树的深度，而集合1~9控制着树的宽度。
- 如果叶子节点里的和等于目标和，就符合要求，返回结果
- 求解组合问题中的剪枝过程，通过对目标集合个数和元素个数的控制，实现了剪枝优化
思路来源于卡尔的代码随想录，文章摘取： 代码随想录 (programmercarl.com)
- targetSum（int）目标和，也就是题目中的n
- k（int）就是题目中要求k个数的集合
- sum（int）为已经收集的元素的总和，也就是path里元素的总和
- startIndex（int）为下一层for循环搜索的起始位置
（1）「回溯」 三部曲：
- ① 首先，确定递归函数的参数和返回值
- ② 确定递归的终止条件
- ③ 确定单层搜索的逻辑
void backtracking(参数) {
if(终止条件) {
存放结果;
return;
}
for(选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
处理节点;
backtracking(路径，选择列表);//递归
回溯，撤销处理结果
}
}- 确定终止条件 k 控制树的深度，通过 startIndex 来控制每一个 for 循环从哪里开始的
class Solution {
public:
vector<vector<int>> result;// 存放结果集
vector<int>path; // 符合条件的结果
void backtracking(int targetSum,int sum,int k,int startIndex) {
if(path.size() == k) {
if(sum == targetSum) {
result.push_back(path);
}
return;// 如果path.size() == k 但sum != targetSum 直接返回
}
for(int i=startIndex;i<=9;i++) {
sum+=i;// 处理
path.push_back(i);// 处理
backtracking(targetSum,sum,k,i+1);// 注意i+1调整startIndex
path.pop_back();// 回溯
sum-=i;// 回溯
}
}
vector<vector<int>> combinationSum3(int k, int n) {
backtracking(n,0,k,1);
return result;
}
};
（2）优化：剪枝
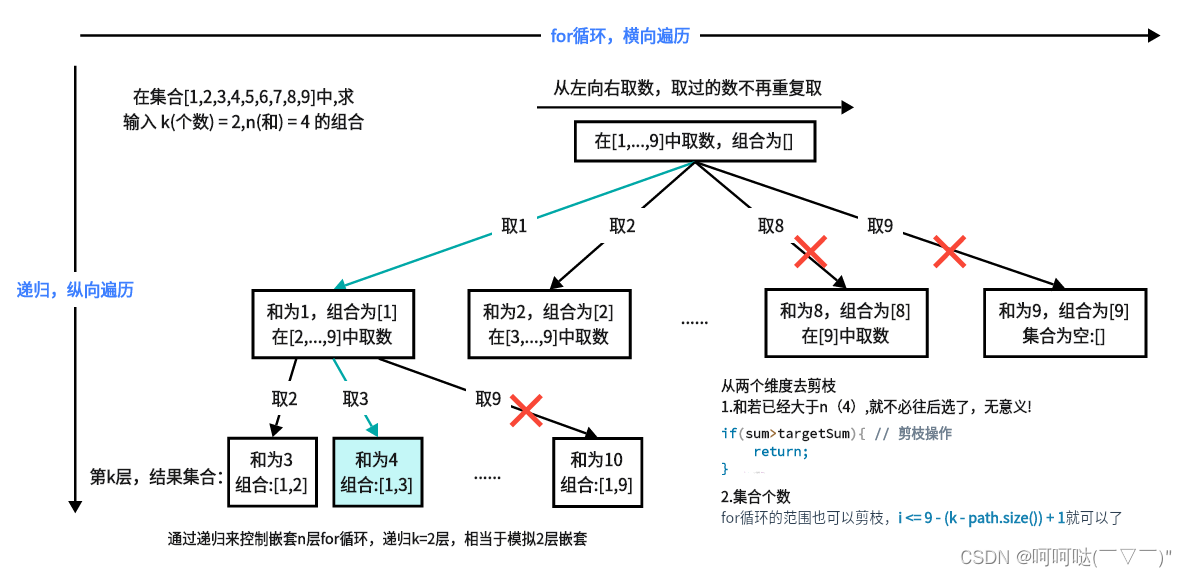
- 通过对目标集合个数和元素个数的控制
- 剪枝过程在for循环中控制，控制组合个数
- 剪枝操作可以减少不必要的递归
class Solution {
public:
vector<vector<int>> result;
vector<int>path;
void backtracking(int targetSum,int sum,int k,int startIndex) {
if(sum>targetSum) { // 剪枝：对目标和
return;
}
if(path.size() == k) {
if(sum == targetSum) {
result.push_back(path);
}
return;
}
for(int i=startIndex;i<=9-(k-path.size())+1;i++) { // 剪枝：对集合个数
sum+=i;
path.push_back(i);
backtracking(targetSum,sum,k,i+1);
path.pop_back();
sum-=i;
}
}
vector<vector<int>> combinationSum3(int k, int n) {
backtracking(n,0,k,1);
return result;
}
};其中，对于 sum > 目标和targetSum 的剪枝也可以写在单层搜索for循环里
class Solution {
public:
vector<vector<int>> result;
vector<int>path;
void backtracking(int targetSum,int sum,int k,int startIndex) {
if(path.size() == k) {
if(sum == targetSum) {
result.push_back(path);
}
return;
}
for(int i=startIndex;i<=9-(k-path.size())+1;i++) {// 剪枝：对集合个数
sum+=i;// 处理
path.push_back(i);// 处理
if(sum>targetSum) { // 剪枝：对目标和
path.pop_back();// 回溯
sum-=i;// 回溯
return;
}
backtracking(targetSum,sum,k,i+1);
path.pop_back();// 回溯
sum-=i;// 回溯
}
}
vector<vector<int>> combinationSum3(int k, int n) {
backtracking(n,0,k,1);
return result;
}
};（3）减少一个参数
class Solution {
public:
vector<vector<int>> result;
vector<int>path;
void backtracking(int targetSum,int k,int startIndex) {
if(path.size() == k) {
if(targetSum==0) {
result.push_back(path);
}
return;
}
for(int i=startIndex;i<=9;i++) {
targetSum-=i;
path.push_back(i);
if(targetSum<0) {
path.pop_back();
targetSum+=i;
return;
}
backtracking(targetSum,k,i+1);
path.pop_back();
targetSum+=i;
}
}
vector<vector<int>> combinationSum3(int k, int n) {
backtracking(n,k,1);
return result;
}
};推荐和参考文章、视频：
和组合问题有啥区别？回溯算法如何剪枝？| LeetCode：216.组合总和III_哔哩哔哩_bilibili
https://www.bilibili.com/video/BV1wg411873x/?spm_id_from=333.788&vd_source=a934d7fc6f47698a29dac90a922ba5a3代码随想录 (programmercarl.com)https://www.programmercarl.com/0216.%E7%BB%84%E5%90%88%E6%80%BB%E5%92%8CIII.html#%E6%80%9D%E8%B7%AF
