🔥博客主页: 小羊失眠啦.
🎥系列专栏:《C语言》 《数据结构》 《Linux》《Cpolar》
❤️感谢大家点赞👍收藏⭐评论✍️

文章目录
- 一、前置说明
- 二、二叉树的遍历
- 2.1 前序遍历
- 2.2 中序遍历
- 2.3 后序遍历
- 2.4 层序遍历
- 三、二叉树的结点个数
- 3.1 二叉树的总结点数
- 3.2 二叉树的叶子结点数
- 3.3 二叉树第k层结点数
- 四、二叉树的高度/深度
- 五、二叉树的查找
- 六、二叉树的创建和销毁
一、前置说明
在学习二叉树各种各样的操作前,我们先来回顾一下二叉树的概念:
二叉树是度不超过2的树,由根结点和左右2个子树组成,每个子树也可以看作一颗二叉树,又可以拆分为根结点和左右两颗子树…
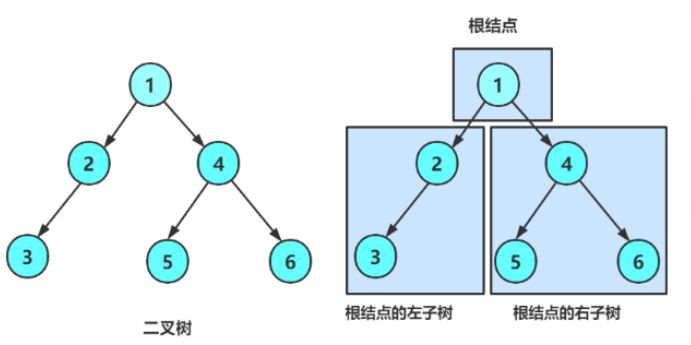
是不是很熟悉,一个大问题可以拆分为两个子问题,每个子问题又可以拆分为更小的子问题,这样层层拆分到不可拆分(遇到空树)的过程,不就是递归吗!因此,我们可以得出:
树是递归定义的,后续树的各种操作正是围绕着这一点进行的。
二、二叉树的遍历
我们先从最简单的操作----遍历学起。所谓二叉树遍历(Traversal)就是按照某种特定的规则,依次对二叉树中的结点进行相应的操作,并且每个节点有且只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。二叉树的遍历分为四种:前序遍历、中序遍历、后序遍历和层序遍历。
2.1 前序遍历
前序遍历(Preorder Traversal)又称先根遍历,即先遍历根结点,再遍历左子树,最后遍历右子树。而对于子树的遍历,也服从上述规则。利用递归,我们可以很快地写出代码:
//前序遍历
void PrevOrder(BTNode* root) {
//遇到空树,递归终点
if (root == NULL) {
printf("NULL ");
return;
}
//对根节点进行操作(此处为打印)
printf("%d ", root->val);
//递归遍历左子树
PrevOrder(root->left);
//递归遍历右子树
PrevOrder(root->right);
}
为了更好地理解这个过程,我们可以画出递归展开图如下:
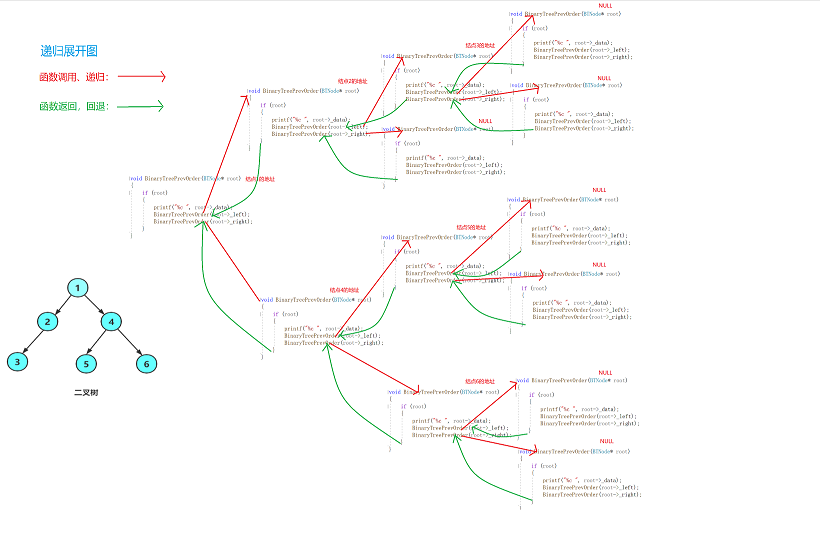
2.2 中序遍历
中序遍历(Inorder Traversal)又称中根遍历,即先遍历左子树,再遍历根结点,最后遍历右子树。同样,子树的遍历规则也是如此。递归代码如下:
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ", root->val);
InOrder(root->right);
}
2.3 后序遍历
后序遍历(Inorder Traversal)又称后根遍历,即先遍历左子树,再遍历右子树,最后遍历根结点。照葫芦画瓢,递归代码如下:
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->val);
}
2.4 层序遍历
除了上面的前中后序遍历,还可以对二叉树进行层序遍历。所谓层序遍历就是从所在二叉树的根节点出发,首先访问第1层的根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推。这样自上而下,自左向右逐层访问树的结点的过程就是层序遍历。
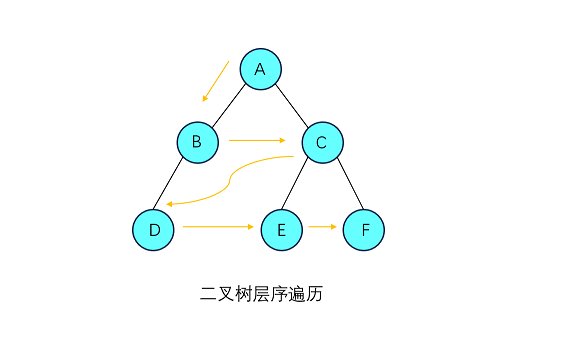
与前面三种遍历不同,层序遍历属于广度优先遍历,因此我们可以利用队列先进先出的特性,将每个结点一层一层依次入队,然后依次出队进行操作即可。具体演示及代码如下:

void LevelOrder(BTNode* root)
{
Que q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
printf("%d ", front->val);
if (front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
QueuePop(&q);
}
printf("\n");
QueueDestroy(&q);
}
三、二叉树的结点个数
3.1 二叉树的总结点数
一颗二叉树的结点数我们可以看作是根结点+左子树结点数+右子树结点数,那左右子树的结点数又是多少呢?按照相同的方法继续拆分,层层递归直到左右子树为空树,返回空树的结点数0即可。递归代码如下:
int TreeSize(BTNode* root)
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
3.2 二叉树的叶子结点数
左右子树都为空的结点即是叶子结点。这里分为两种情况:左右子树都为空和左右子树不都为空。
-
当左右子树都为空时,则这颗树的叶子结点数为1(根节点)。
-
当左右子树不都为空,即根结点不是叶子结点时,这棵树的叶子结点数就为
左子树叶子结点数+右子树叶子结点数(空树没有叶子结点)。
int TreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
3.3 二叉树第k层结点数
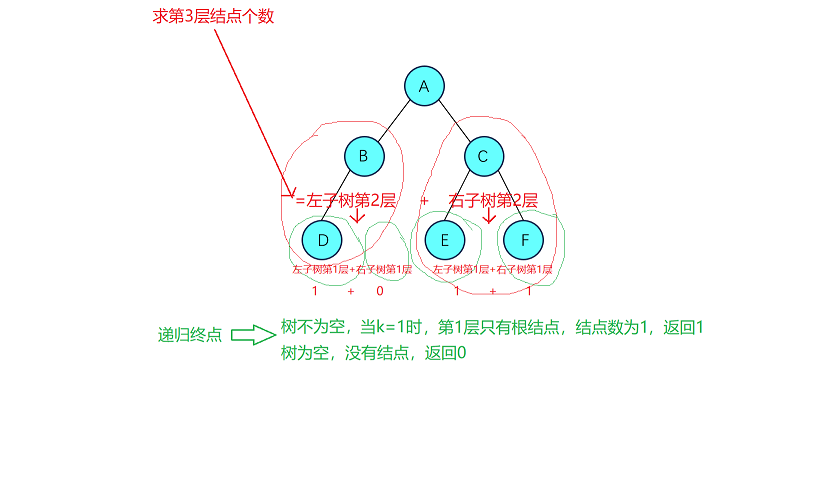
类似的,一颗树第k层的结点数我们可以拆分为其左子树第k-1层结点+右子树第k-1层结点。这样层层递归下去,直到k==1求树的第1层结点数时返回1(树的第1层只有根结点),而如果在递归过程中遇到空树就返回0(空树没有结点)。例如下面一颗树:
int TreeKLevel(BTNode* root, int k)
{
assert(k > 0);
if (root == NULL)
return 0;
if (k == 1)
{
return 1;
}
return TreeKLevel(root->left, k - 1)
+ TreeKLevel(root->right, k - 1);
}

四、二叉树的高度/深度
树中结点的最大层次称为二叉树的高度。因此,一颗二叉树的高度我们可以看作是
1(根结点)+左右子树高度的较大值。层层递归下去直到遇到空树返回0即可,递归代码如下:
int TreeHeight(BTNode* root)
{
if (root == NULL)
return 0;
return fmax(TreeHeight(root->left), TreeHeight(root->right)) + 1;
}

五、二叉树的查找
二叉树的查找本质上就是一种遍历,只不过是将之前的打印操作换为查找操作而已。我们可以使用前序遍历来进行查找,先比较根结点是否为我们要查找的结点,如果是,之间返回;如果不是,遍历左子树和右子树,返回其查找的结果;如果都找不到,返回空指针。代码如下:
// 二叉树查找值为x的结点
BTNode* TreeFind(BTNode* root, int x)
{
if (root == NULL)
return NULL;
if (root->val == x)
return root;
BTNode* ret = NULL;
ret = TreeFind(root->left, x);
if (ret)
return ret;
ret = TreeFind(root->right, x);
if (ret)
return ret;
return NULL;
}
六、二叉树的创建和销毁
最后,我们再来看看如何来创建和销毁一颗二叉树。我们前面说过:二叉树是递归定义的。有了前面的基础,二叉树的创建和销毁也就不是什么难事了。
BTNode* BuyNode(int x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail");
exit(-1);
}
node->val = x;
node->left = NULL;
node->right = NULL;
return node;
}
// 二叉树销毁
void TreeDestroy(BTNode* root)
{
if (root == NULL)
{
return;
}
TreeDestroy(root->left);
TreeDestroy(root->right);
free(root);
//root = NULL;
}
本次的内容到这里就结束啦。希望大家阅读完可以有所收获,同时也感谢各位铁汁们的支持。文章有任何问题可以在评论区留言,小羊一定认真修改,写出更好的文章~~