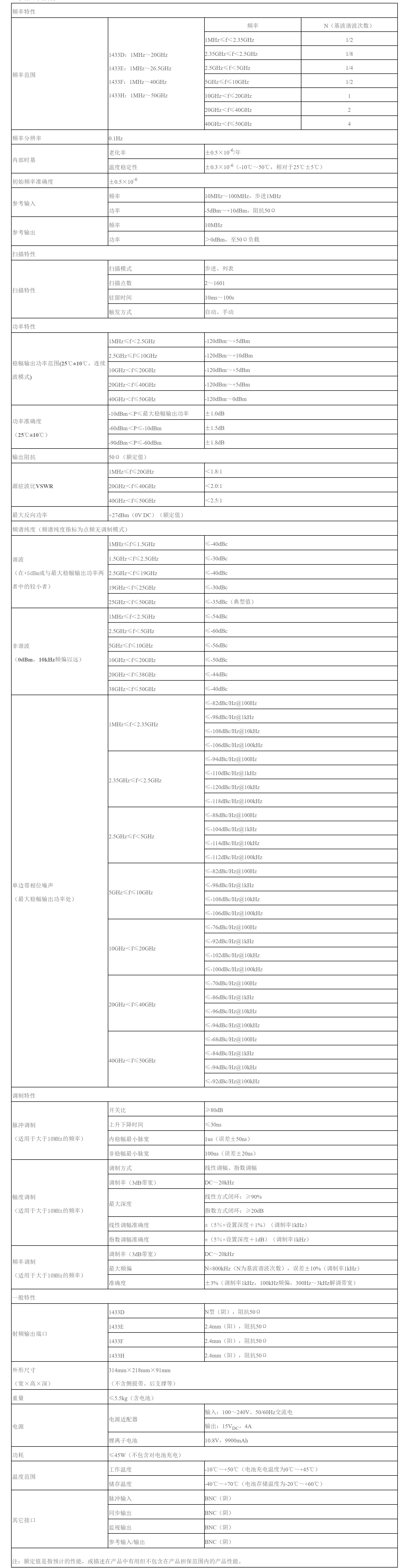
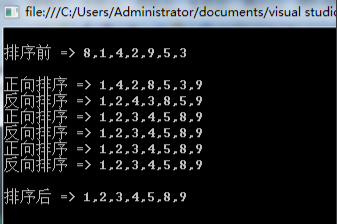
IIP3参数的含义
三阶交调频率分量
混频器的输入端的总输入信号通常由射频输入(载波+被调制信号)和本振组成。以输入总信号由3个正弦信号为例,输入端的总输入信号为:
u
=
u
1
cos
ω
1
t
+
u
2
cos
ω
2
t
+
u
3
cos
ω
3
t
\begin{aligned} u=u_1\cos\omega_1t+u_2\cos\omega_2t+u_3\cos\omega_3t \end{aligned}
u=u1cosω1t+u2cosω2t+u3cosω3t
混频器的非线性特性常用多项式逼近来进行描述,即:
i
=
a
0
+
a
1
u
+
a
2
u
2
+
a
3
u
3
+
⋯
\begin{aligned} i=a_0+a_1u+a_2u^2+a_3u^3+\cdots \end{aligned}
i=a0+a1u+a2u2+a3u3+⋯
两式联立整理后可以得到:
i
=
a
0
+
a
1
(
u
1
cos
ω
1
t
+
u
2
cos
ω
2
t
+
u
3
cos
ω
3
t
)
+
a
2
(
u
1
2
cos
2
ω
1
t
+
u
2
2
cos
2
ω
2
t
+
u
3
2
cos
2
ω
3
t
)
+
a
3
(
u
1
3
cos
3
ω
1
t
+
u
2
3
cos
3
ω
2
t
+
u
3
3
cos
3
ω
3
t
)
+
⋯
+
a
p
cos
(
±
ω
3
+
ω
1
)
t
+
a
q
cos
(
±
ω
3
±
ω
2
)
t
+
a
m
cos
(
±
ω
3
+
2
ω
1
±
ω
2
)
t
+
a
n
cos
(
±
ω
3
+
ω
1
±
2
ω
2
)
t
+
a
x
cos
(
k
ω
3
+
r
ω
1
+
s
ω
2
)
t
+
⋯
\begin{aligned} i&=a_0 \\ &+a_1(u_1\cos\omega_1t+u_2\cos\omega_2t+u_3\cos\omega_3t) \\ &+a_2(u_1^2\cos2\omega_1t+u_2^2\cos2\omega_2t+u_3^2\cos2\omega_3t) \\ &+a_3(u_1^3\cos3\omega_1t+u_2^3\cos3\omega_2t+u_3^3\cos3\omega_3t) \\ &+\cdots \\ &+a_p\cos(\pm\omega_3+\omega_1)t+a_q\cos(\pm\omega_3\pm\omega_2)t \\ &+a_m\cos(\pm\omega_3+2\omega_1\pm\omega_2)t \\ &+a_n\cos(\pm\omega_3+\omega_1\pm2\omega_2)t \\ &+a_x\cos(k\omega_3+r\omega_1+s\omega2)t \\ &+\cdots \end{aligned}
i=a0+a1(u1cosω1t+u2cosω2t+u3cosω3t)+a2(u12cos2ω1t+u22cos2ω2t+u32cos2ω3t)+a3(u13cos3ω1t+u23cos3ω2t+u33cos3ω3t)+⋯+apcos(±ω3+ω1)t+aqcos(±ω3±ω2)t+amcos(±ω3+2ω1±ω2)t+ancos(±ω3+ω1±2ω2)t+axcos(kω3+rω1+sω2)t+⋯
其中a0为直流项,a1为基波项,a2为2次谐波项,a3为3次谐波项,高次谐波已忽略。这些分量均可通过滤波器滤除,一般不会造成太大影响。
ap和aq项为有用的中频分量,需要保留。
am和an称为 三阶交调频率分量 ,它们由混频器非线性特性的3次方项产生,且难以通过滤波器滤除。称为 三阶交调失真干扰。
三阶交调截点(IP3)
因为三阶交调频率分量由混频器非线性特性的3次方项产生,所以通常输入信号功率增加1dB时,三阶交调失真干扰的功率就要增加3dB,而正常的中频输出的功率与输入信号功率大致成线性关系。当三阶交调失真干扰的功率(四阶及以上一般幅度较小,且可以通过滤波器或电路设计进行有效的抑制)与中频输出信号的功率相等时,将无法进行正常通信,此时,该交叉点称为三阶交调截点。三阶交调截点如图所示。
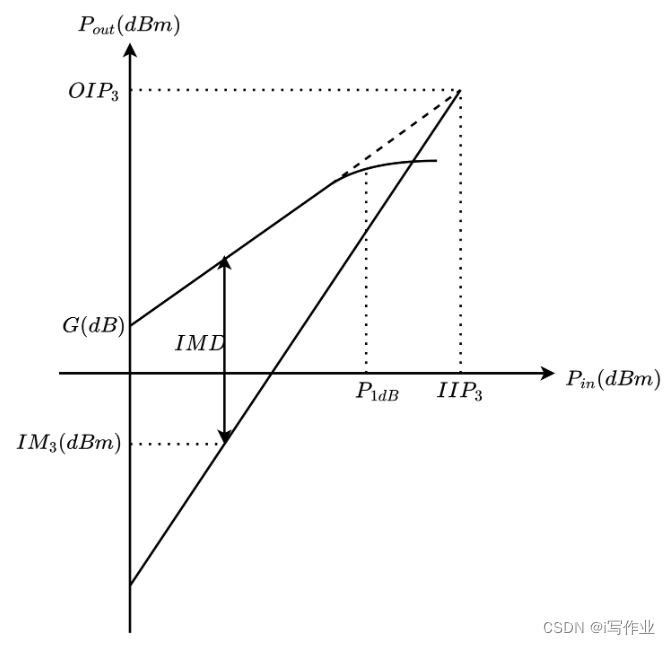
IIP3(Input 3rd Order Intercept Point)
三阶交调截点 IP3定义为三阶交调功率达到和基波功率相等的点,此点对应的输入功率为IIP3,输出功率为OIP3。
如图可见IIP3(dBm)越大,表明混频器的线性范围越宽。
IIP3还与本振功率电平有关,本振电平增加,混频器中的二极管、三极管、场效应管的线性工作区加大,混频器的线性性能提升,三阶交调失真减小,IIP3上升。
线性度提高,三阶交调分量的系数会减小,导致三阶交调分量的曲线会向下平移,所以导致IIP3上升。
器件参数上标明的IIP3是标准本振功率电平下的IIP3参数。