Problem: 113. 路径总和 II
文章目录
- 题目描述
- 思路
- 解题方法
- 复杂度
- 代码实现细节处
- Code
题目描述
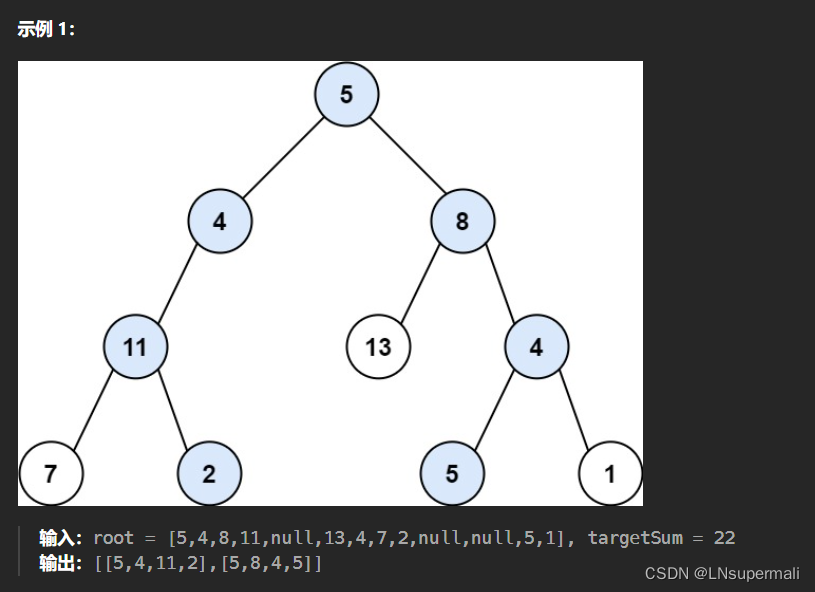
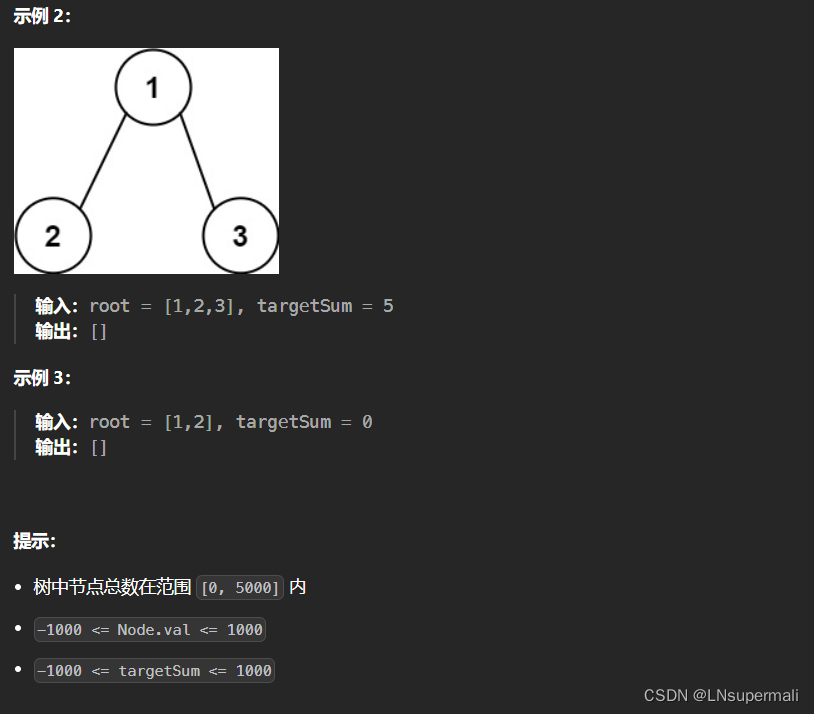
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
思路
题目要求找出所有从根节点到叶子节点的路径总和,这一点很容易让我们联想到使用DFS来求解本题。
按先序遍历的顺序递归遍历二叉树,当遍历到二叉树的叶子节点时判断当前路径所有元素和是否等于题目所给的targetSum。
解题方法
1.定义成员变量List<List> result用于记录并返回最终的二维结果数组
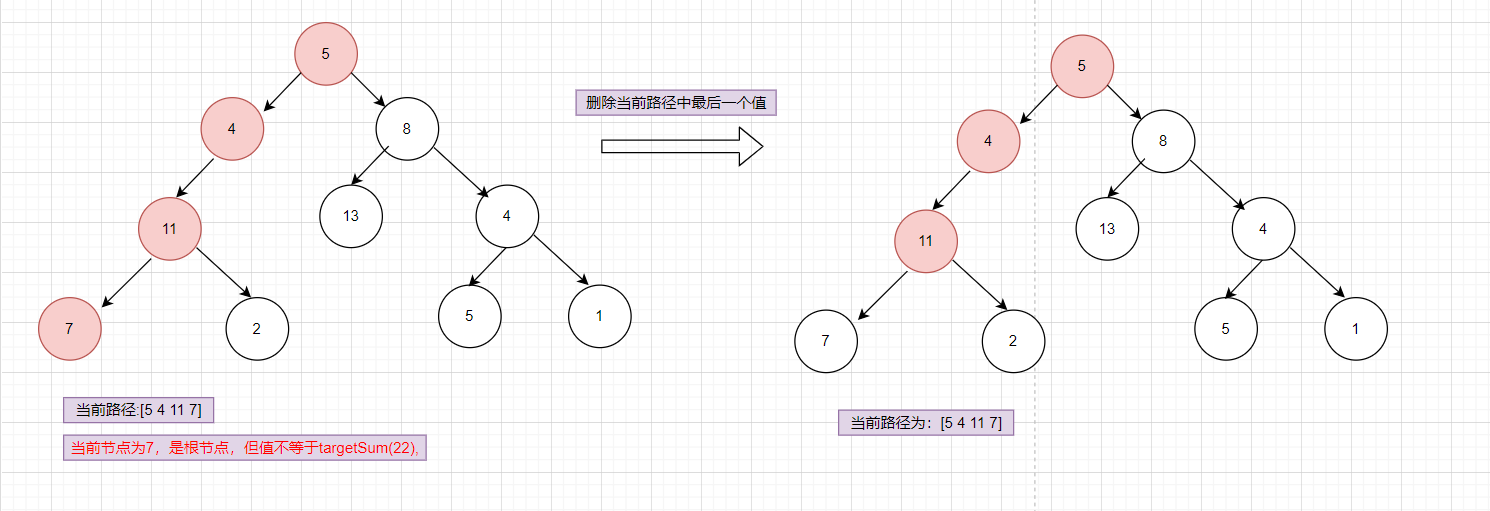
2.编写深度优先函数,找出所有的符合条件的路径。2.1.每次先将当前节点添加到当前的路劲当中,并判断当前节点是否为叶子节点;若为叶子节点再判断当前的路径上所有节点值之和是否等于给定的targetSum,若等于则将当前路径添加到最终的结果集合result,若当前节点为叶子节点但路径上所有节点值之和不等于targetSum则将当前用于记录路径的数组的最后一位去掉。
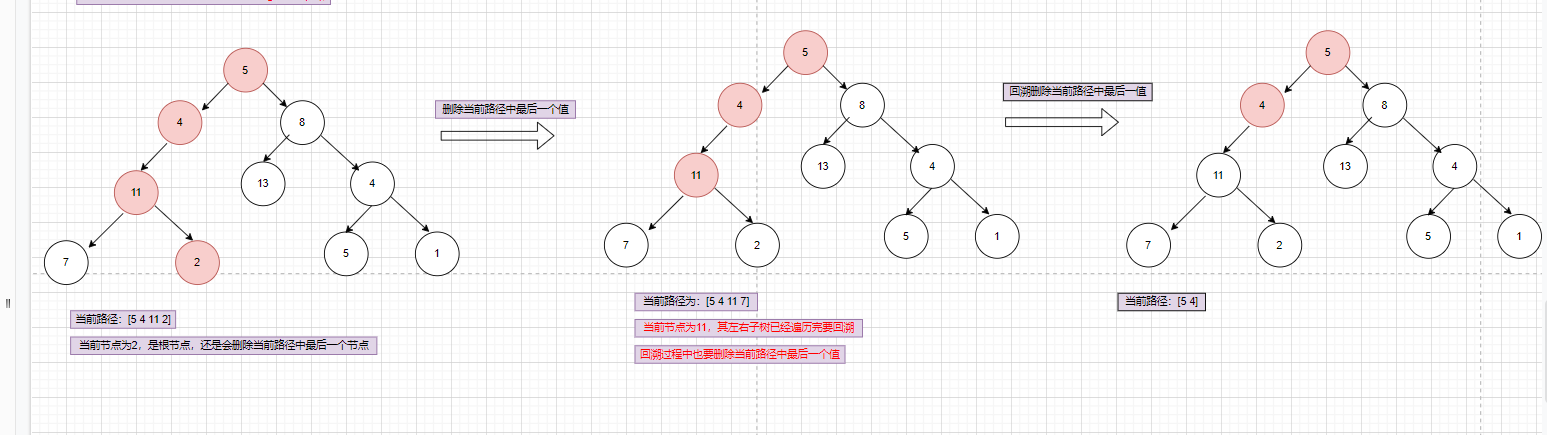
2.2.递归当前节点的左子树和右子树,在归的过程中由于要回溯到上一层节点,所以也要将当前用于记录路径的数组的最后一位去掉!!!
复杂度
时间复杂度:
O ( n 2 ) O(n^2) O(n2)
空间复杂度:
O ( n ) O(n) O(n)
代码实现细节处
1.若当前节点为叶子节点但路径上所有节点值之和不等于targetSum则将当前用于记录路径的数组的最后一位去掉;
2.在归的过程中由于要回溯到上一层节点,所以也要将当前用于记录路径的数组的最后一位去掉!!!
Code
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
//最终结果集合
public List<List<Integer>> result;
/**
* @param root 树的根节点
* @param targetSum 目标值
* @return List<List < Integer>>
*/
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
result = new ArrayList<>();
if (root == null) {
return result;
}
depthFirstSearch(root, targetSum, new ArrayList<>(), 0);
return result;
}
/**
* 深度优先函数,找出所有的符合条件的路径
*
* @param root 树的根节点
* @param sum 给定的targetSum
* @param path 用于记录一路径的数组
* @param pathSum 当前路径上的所有元素值之和
*/
private void depthFirstSearch(TreeNode root, int sum, List<Integer> path, int pathSum) {
//先将当前节点值添加到路径集合
path.add(root.val);
//已经递归到根节点
if (root.left == null && root.right == null) {
//当前路径值等于所给目标值
if (pathSum + root.val == sum) {
List<Integer> foundPath = new ArrayList<>();
foundPath.addAll(path);
result.add(foundPath);
}
//路径已经最大,需处理
path.remove(path.size() - 1);
return;
}
if (root.left != null) {
depthFirstSearch(root.left, sum, path, pathSum + root.val);
}
if (root.right != null) {
depthFirstSearch(root.right, sum, path, pathSum + root.val);
}
//回退过程中需要再次处理路径
path.remove(path.size() - 1);
}
}