51单片机蜂鸣器发出悦耳的声音
1.概述
这篇文章介绍单片机控制蜂鸣器入门小实验,通过该实验掌握蜂鸣器发声的原理,控制声音发出我们想听的音乐。
2.蜂鸣器发声
2.1.硬件原理
1.蜂鸣器正极接单片机20号引脚VCC,负极接19号引脚P1.7
2.20MHZ晶振分别接单片机4、5引脚XTAL2和XTAL1
3.晶振每个引脚各接一个30pf电容到单片机10号引脚GND

2.2.蜂鸣器发声代码
在main函数中通过修改DELAY_MS()延迟函数的数值观察蜂鸣器有什么变化,通过实际感受了解电流频率的变化如何改变蜂鸣器的发声。
/*************************************************************
* 程序名:控制蜂鸣器发声
* 编写人:bruce
* 日 期:2023-11-26
* 修改日志:开始编写
/*************************************************************/
#include<STC12C2052AD.H>
sbit BEEP = P1^7;
/*********************************************************************************************
函数名:毫秒级CPU延时函数
调 用:DELAY_MS (?);
参 数:1~65535(参数不可为0)
返回值:无
结 果:占用CPU方式延时与参数数值相同的毫秒时间
备 注:应用于1T单片机时i<600,应用于12T单片机时i<125
/*********************************************************************************************/
void DELAY_MS (unsigned int a){
unsigned int i;
while( --a != 0){
for(i = 0; i < 600; i++);
}
}
void main(){
while(1){
BEEP = 1;
DELAY_MS(2);
BEEP = 0;
DELAY_MS(2);
}
}
3.电子琴
通过单片机控制电流中数字信号方波的宽度,实现蜂鸣器发出不同的声音。
3.1.按键电子琴
1.硬件原理
根据电路原理图和实物图将硬件接好。
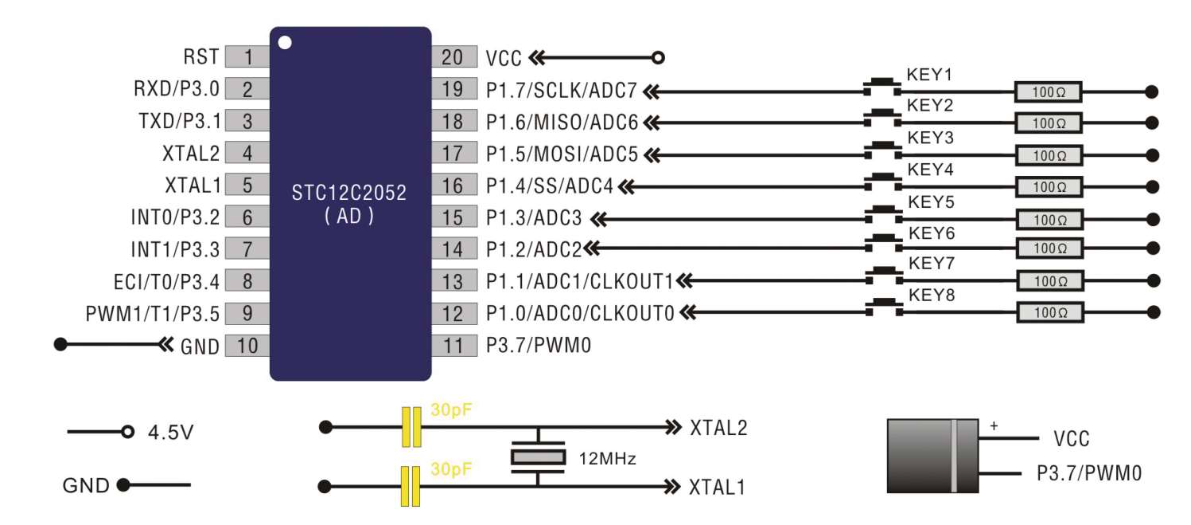

2.八键电子琴程序
/*************************************************************
* 程序名:控制蜂鸣器发声
* 编写人:bruce
* 日 期:2023-11-26
* 修改日志:开始编写
/*************************************************************/
#include<STC12C2052AD.H>
sbit SPEAKER = P3^7;
#define KEY P1
unsigned char MUSIC;
unsigned char STH0;
unsigned char STL0;
// tab数组中的值是乐谱中音调对应HZ频率值
unsigned int code tab[]={
64021,64103,64260,64400,//低音3开始
64524,64580,64684,64777,
64820,64898,64968,65030,
65058,65110,65157,65178
};
void main(void){
TMOD=0x01;
ET0=1;
EA=1;
KEY = 0xff;
while(1){
if(KEY != 0xff){
switch (~KEY){//显示的列位置
case 0x01://
MUSIC = 7;
break;//
case 0x02://
MUSIC = 6;
break;//
case 0x04://
MUSIC = 5;
break;//
case 0x08://
MUSIC = 4;
break;//
case 0x10://
MUSIC = 3;
break;//
case 0x20://
MUSIC = 2;
break;//
case 0x40://
MUSIC = 1;
break;//
case 0x80://
MUSIC = 0;
break;//
}
// 用数组的值/256获取十六进制的值
STH0=tab[MUSIC]/256;
STL0=tab[MUSIC]%256;
TR0=1;
}else{
SPEAKER = 1;
TR0=0;
}
}
}
// 定义计数器的起始值,来控制电流方形波的宽度,改变发声的音调。
void t0(void) interrupt 1 using 0{
TH0=STH0;
TL0=STL0;
SPEAKER=~SPEAKER;
}