文章目录
- 【强化学习】动态规划算法实践
- 一. 实验过程
- 1.1 Environment
- 1.2 Policy Iteration
- 1.3 Policy Evaluation
- 1.4 Policy Improvement
- 1.5 Value Iteration
- 二. 实验结果与分析
- 2.1 分析Policy Iteration和Value Iteration收敛误差随着迭代次数的分布曲线
【强化学习】动态规划算法实践
阅读本文的前置条件:
前置知识概念:状态价值函数 v v v、动作价值函数 p p p
前置方法概念:
- 策略迭代Policy Iteration(内含策略评估Policy Evaluation + 策略优化Policy Improvement)
- 价值迭代Value Iteration
实验环境如下:16个格子,走到左上或者右下角即为结束。否则持续行走,每走一步奖励-1。
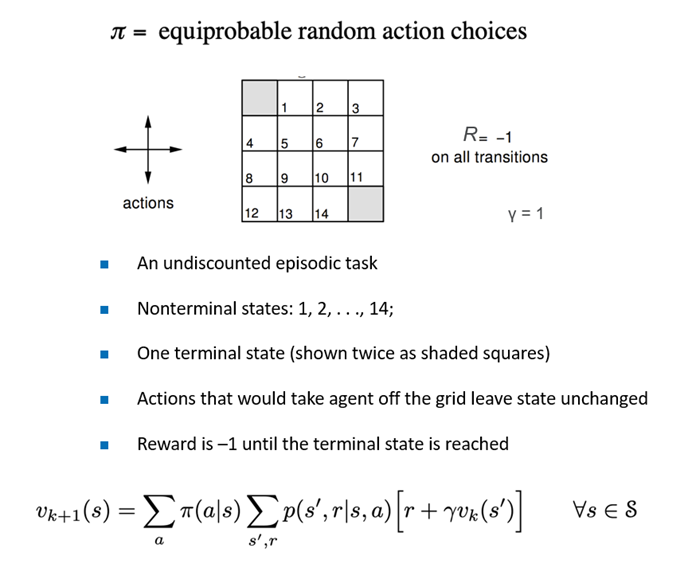
给定初始随机策略和状态价值函数 v 0 v_0 v0:

针对上述Gridworld问题编码实现:
- 使用 Policy Evaluation的方法计算 v π v_\pi vπ
- 用Policy Iteration方法搜索最优 v ∗ v_* v∗, p ∗ p_* p∗
- 用Value Iteration方法搜索最优 v ∗ v_* v∗, p ∗ p_* p∗
一. 实验过程
本节实验过程将分为环境准备、策略迭代、策略评估、策略提升、价值迭代五个部分。
1.1 Environment
由PPT中的Gridworld问题:
- 4*4的网格,左上和右下角为目标点。
- 每次移动reward = -1,到达目标点无需移动。
- 如果移动越界,则位置不变。
我们定义如下Gridworld类表示网格世界。
class GridWorld:
""" 网格世界,坐标系原点(0,0)
"""
def __init__(self, ncol=4, nrow=4):
self.ncol = ncol # 定义网格世界的列
self.nrow = nrow # 定义网格世界的行
self.target_grids = [(0, 0), (ncol-1, nrow-1)] # 存储目标区域
# 状态数量
self.state_nums = ncol * nrow
# 4种动作, actions[0]:上,actions[1]:下, actions[2]:左, actions[3]:右。
self.actions = [[0, -1], [0, 1], [-1, 0], [1, 0]]
# 状态转移概率矩阵P[state][action] = [(p, next_state, reward, done)]包含下一个状态和奖励
# state 是一维表示的
self.P = self.init_P()
其中,除了基本的行和列之外,我们定义上下左右的四个动作,以及状态转移概率矩阵P。P矩阵表示在状态state中采取动作action后,多大的概率获得多少奖励以及进入下一个状态,是否结束。
由于本次实验环境中一种行动对应的下一个状态只有一种,且定义了除目标点之外的移动均会获得-1的奖励。故此处的p固定为1,对应下节Bellman方程中的 p ( s ′ , r ∣ s , a ) p(s',r|s,a) p(s′,r∣s,a)。
为便于计算,我们将二维的4*4网格状态通过一维的线性表示。如 s t a t e = ( x , y ) state = (x,y) state=(x,y)可以表示为 s t a t e = x ∗ n c o l + y state = x * ncol + y state=x∗ncol+y;
状态转移概率矩阵初始化如下:
def init_P(self):
# 初始化
P = [[[] for j in range(4)] for i in range(self.state_nums)]
for i in range(self.nrow):
for j in range(self.ncol):
# 遍历四个方向
for a in range(4):
# 采取行动后进入的状态s'、奖励r都是固定的概率1
psa = 1
# 位置在目标状态,因为不需要继续交互,任何动作奖励都为0
if (i, j) in self.target_grids:
P[i * self.ncol +
j][a] = [(psa, i * self.ncol + j, 0, True)]
continue
# 其他位置(边界越界后依旧保持不动)
next_x = min(self.ncol - 1, max(0, j + self.actions[a][0]))
next_y = min(self.nrow - 1, max(0, i + self.actions[a][1]))
next_state = next_y * self.ncol + next_x
reward = -1
done = False
# 如果下一个位置在目标状态,Done
if (next_x, next_y) in self.target_grids:
done = True
P[i * self.ncol + j][a] = [(psa, next_state, reward, done)]
return P
1.2 Policy Iteration
b) 用Policy Iteration方法搜索最优 v ∗ 、 p ∗ v_*、\ p_* v∗、 p∗
策略迭代算法的过程如下:对当前的策略进行策略评估,得到其状态价值函数,然后根据该状态价值函数进行策略提升以得到一个更好的新策略,接着继续评估新策略、提升策略……直至最后收敛到最优策略
我们判定,若迭代过程中,旧策略等于新策略,则视为收敛,并且此时的策略即是 p ∗ p* p∗。
同理当 v k + 1 v_{k+1} vk+1和 v k v_k vk相同(相差小于阈值θ)时,它就是贝尔曼最优方程的不动点,对应最优状态价值函数 v ∗ v* v∗
P o l i c y I t e r a t i o n Policy Iteration PolicyIteration过程如下:

P o l i c y I t e r a t i o n Policy Iteration PolicyIteration 框架代码如下:
def policy_iteration(self): # 策略迭代
# V及pi的初始化已完成(具体赋值见1.3)
while 1:
self.policy_evaluation()
old_pi = copy.deepcopy(self.pi) # 将列表进行深拷贝,方便接下来进行比较
new_pi = self.policy_improvement()
if old_pi == new_pi:
break
其中1.3节将具体说明policy_evaluation、1.4节将具体说明policy_improvment。
1.3 Policy Evaluation
a) 用本PPT讲的 Policy Evaluation的方法计算 v π v_\pi vπ
对于状态价值函数的Bellman方程如下:
v
π
(
s
)
=
∑
a
π
(
a
∣
s
)
∑
s
′
,
r
p
(
s
′
,
r
∣
s
,
a
)
[
r
+
γ
v
π
(
s
′
)
]
v_\pi(s) = \sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)[r+\gamma v_\pi(s')]
vπ(s)=a∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γvπ(s′)]
由此可知我们后续实现自举方式时所用到的状态价值函数递推式:
v
k
+
1
(
s
)
=
∑
a
π
(
a
∣
s
)
∑
s
′
,
r
p
(
s
′
,
r
∣
s
,
a
)
[
r
+
γ
v
k
(
s
′
)
]
v_{k+1}(s) = \sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)[r+\gamma v_k(s')]
vk+1(s)=a∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γvk(s′)]
为此,我们实现的基本步骤如下:
-
初始化值函数
对于所有的初始状态s,我们只需要设置其状态价值v为0即可。
-
迭代更新状态价值函数
对于每一个状态s,我们使用贝尔曼方程计算新的值函数new_v。
-
检查收敛
检查状态价值函数的更新是否收敛于我们定义的阈值θ,若收敛则停止迭代。最新的new_v即为所求。
由上述递推式可知,我们需要预先知道并且定义好如下变量:
-
A:表示动作空间。a表示特定的动作。在本次实验中动作空间定义如下:
a c t i o n s = [ [ 0 , − 1 ] , [ 0 , 1 ] , [ − 1 , 0 ] , [ 1 , 0 ] ] actions = [[0, -1], [0, 1], [-1, 0], [1, 0]] actions=[[0,−1],[0,1],[−1,0],[1,0]]
分别表示上下左右四个方向的行动。 -
π ( a ∣ s ) \pi(a|s) π(a∣s):策略在状态s下采取行动a的概率。我们定义在初始策略中,每一个状态下等概率随机采取行动,即:
π = [ [ 0.25 , 0.25 , 0.25 , 0.25 ] ∗ s t a t e n u m s ] \pi = [[0.25, 0.25, 0.25, 0.25] * state\ nums] π=[[0.25,0.25,0.25,0.25]∗state nums] -
P ( s ′ , r ∣ s , a ) P(s',r|s,a) P(s′,r∣s,a):策略在状态s下采取行动a后进入状态s’以及获得奖励r的概率。由于本次实验环境较为简单,采取行动后进入的状态s’只有一种,且采取行动a获取的奖励r也是固定为-1(除了目标点之外),故可直接视为1。
-
γ \gamma γ:未来的折扣因子。在当前实验中,我们设置为1。
-
v k ( s ) v_k(s) vk(s):s状态下的价值函数。在初始化后,我们定义每个状态初始都是价值为0。
v = [ 0 ] ∗ s t a t e n u m s v = [0] * state\ nums v=[0]∗state nums -
θ:收敛阈值。用于判定状态价值函数是否收敛。我们设置为0.001。
至此,我们可以构建Policy Evaluation方法来计算 v π v_\pi vπ,代码如下:
def policy_evaluation(self): # 策略评估
state_nums = self.env.state_nums
while 1:
max_diff = 0
new_v = [0] * state_nums # 初始化值函数
for s in range(state_nums):
qsa_list = [] # 状态s下的所有Q(s,a)价值
# 尝试这个状态的所有动作
for a in range(4):
qsa = 0
for res in self.env.P[s][a]:
p, next_state, r, done = res
# 应用贝尔曼方程的右侧部分
qsa += p * (r + self.gamma * self.v[next_state])
qsa_list.append(self.pi[s][a] * qsa)
# 最后累加即得到v_{k+1}
new_v[s] = sum(qsa_list)
max_diff = max(max_diff, abs(new_v[s] - self.v[s]))
self.v = new_v # 自举
if max_diff < self.theta:
break # 满足收敛条件,退出评估迭代
为了验证正确性,我们在每次自举之后输出状态价值函数,输出结果(部分)如下:
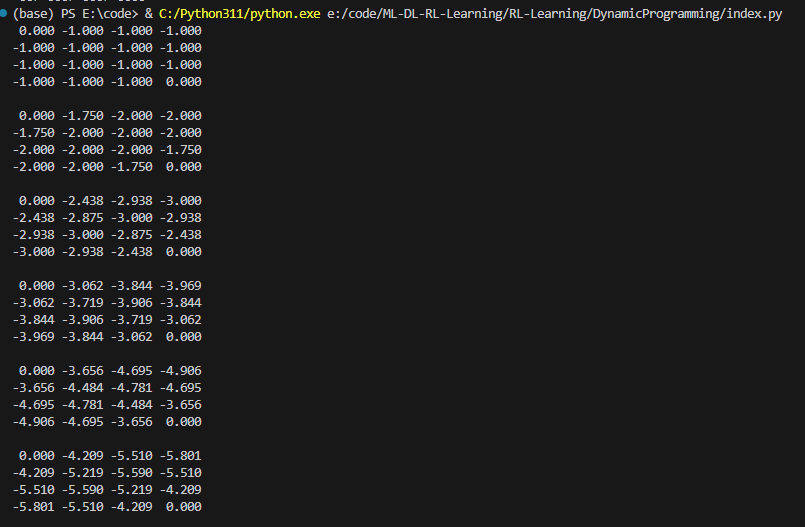
我们取第二次输出的(0,1)位置上的-1.750 进行验证:
−
1.750
=
[
0.25
∗
(
−
1
+
1
∗
(
−
1
)
)
]
+
[
0.25
∗
(
−
1
+
1
∗
(
−
1
)
)
]
+
[
0.25
∗
(
−
1
+
1
∗
(
−
1
)
)
]
+
[
0.25
∗
(
−
1
+
1
∗
(
0
)
)
]
\\ -1.750 = [0.25*(-1 + 1*(-1))] + [0.25*(-1 + 1*(-1))]+ \\ [0.25*(-1 + 1*(-1))] + [0.25*(-1 + 1*(0))]
−1.750=[0.25∗(−1+1∗(−1))]+[0.25∗(−1+1∗(−1))]+[0.25∗(−1+1∗(−1))]+[0.25∗(−1+1∗(0))]
符合贝尔曼递推式。
1.4 Policy Improvement
策略提升的基本步骤为:
-
初始化新策略:
- 对每个状态s,初始化一个新的动作a。
-
对每个状态进行策略改进:
- 对每个状态 s
- 对所有可能的动作 a
- 计算选择动作 a 后的价值 Q(s*,*a)
- 对所有可能的动作 a
- 对每个状态 s
-
选择最优动作:
- 对于每个状态s ,选择使得 Q(s,a) 最大的动作 a 。
-
更新策略:
-
使用新的动作作为当前策略,得到改进后的策略。
(由于可能存在多个相同价值的动作,所以我们将相同数量的最大动作价值转为概率,赋值给新的策略pi。
-
# 策略提升
def policy_improvement(self):
state_nums = self.env.state_nums
for s in range(state_nums):
qsa_list = []
for a in range(4):
qsa = 0
for res in self.env.P[s][a]:
p, next_state, r, done = res
qsa += p * (r + self.gamma * self.v[next_state])
qsa_list.append(qsa)
maxq = max(qsa_list)
cntq = qsa_list.count(maxq) # 计算有几个动作得到了最大的Q值
# 让这些动作均分概率
self.pi[s] = [1 / cntq if q == maxq else 0 for q in qsa_list]
print(f"state: {s} pi: {self.pi[s]}")
print("策略提升完成")
return self.pi
我们打印当前策略在每个状态下的价值以及智能体可采取的动作。
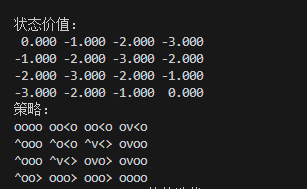
参考《动手学强化学习》输出示例,我们使用一个箭头序列来表示可能采取的行动。o表示不采取行动。例如:
^v<>:表示等概率采取上下左右。^o<o:表示等概率采取向左和向上两种动作。ooo>:表示在当前状态只采取向右动作。oooo:表示不采取行动。(目标点才有)
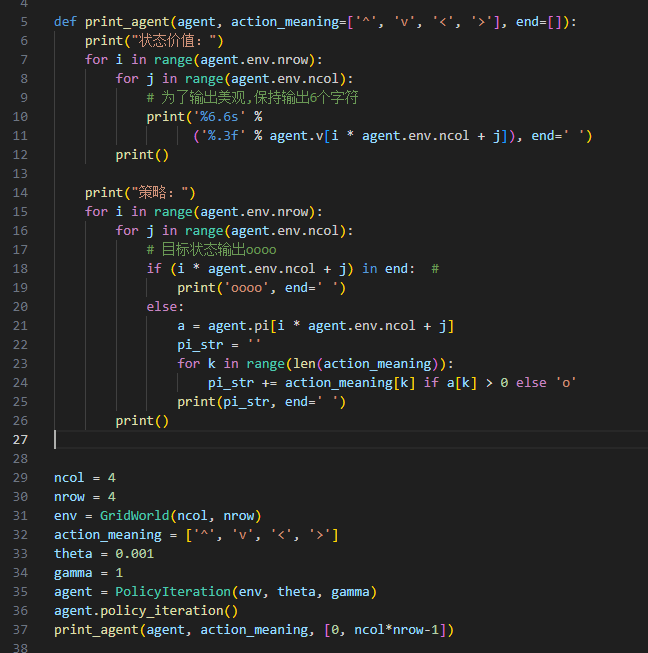
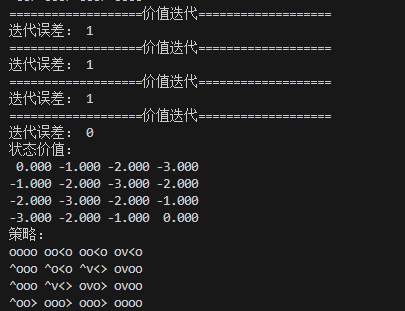
结束第一轮策略评估后:我们得到如下的状态价值,并且在策略提升后,可以看到每个状态点会朝着具有最大状态价值的节点行走的策略。
(策略数组表示选择 [上,下,左,右] 行动的概率。)
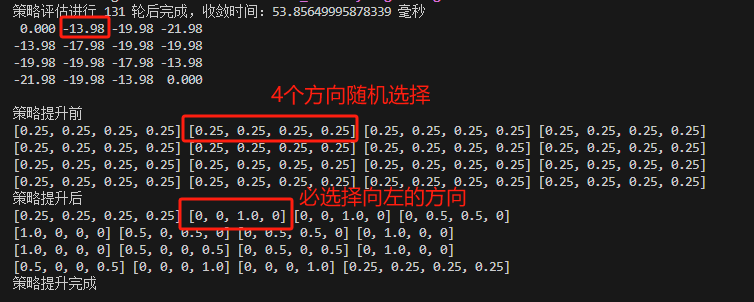
策略评估与策略提升交替迭代3次后,收敛输出如下:
1.5 Value Iteration
Policy Iteration需要等待policy evaluation完成,使得状态价值函数收敛后才进行Policy Improvement。然后随着状态增多,策略评估的收敛速度变慢,我们不必每次都等待状态价值函数完全收敛才提升策略。
Value Iteration的核心思想就是,我们只进行一次policy evaluation,而不必等待状态价值函数收敛。
但是需要注意的是,价值迭代中不存在显式的策略,我们只维护一个状态价值函数。
相比于策略迭代的递推式:
v
k
+
1
(
s
)
=
∑
a
π
(
a
∣
s
)
∑
s
′
,
r
p
(
s
′
,
r
∣
s
,
a
)
[
r
+
γ
v
k
(
s
′
)
]
v_{k+1}(s) = \sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)[r+\gamma v_k(s')]
vk+1(s)=a∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γvk(s′)]
价值迭代递推式如下:
v
k
+
1
(
s
)
=
max
a
∑
s
′
,
r
p
(
s
′
,
r
∣
s
,
a
)
[
r
+
γ
v
k
(
s
′
)
]
v_{k+1}(s) = \max_a\sum_{s',r}p(s',r|s,a)[r+\gamma v_k(s')]
vk+1(s)=amaxs′,r∑p(s′,r∣s,a)[r+γvk(s′)]
算法流程如下:

初始化及循环代码如下:
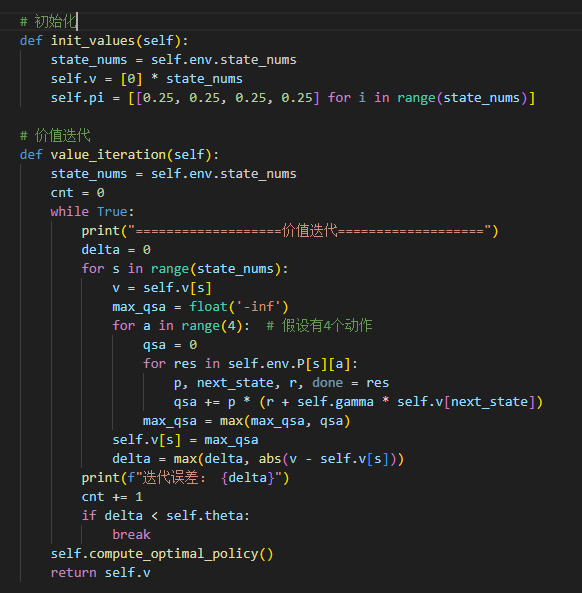
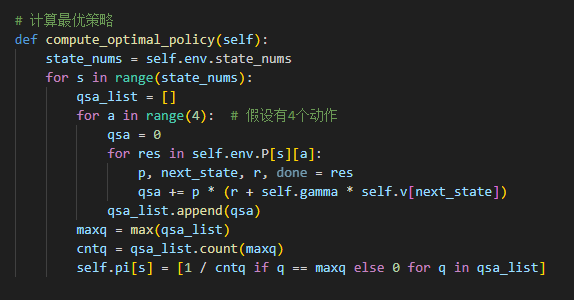
结束循环后,计算最优的确定性策略(若出现多个最大值,则等概率取最大。)
在经历4次迭代后,收敛到与策略迭代相同的最优解:
二. 实验结果与分析
(其余内容分析较烂,就只展示收敛误差吧。)
2.1 分析Policy Iteration和Value Iteration收敛误差随着迭代次数的分布曲线
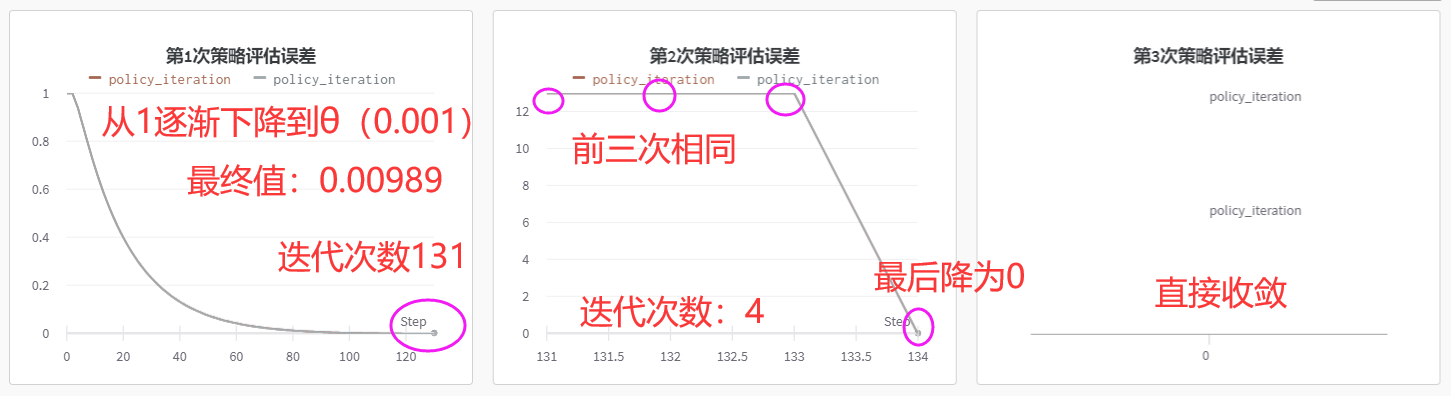
我们使用wandb库进行可视化状态价值函数的收敛情况,在策略迭代中的三次交替过程中,收敛误差随迭代次数分布如下:
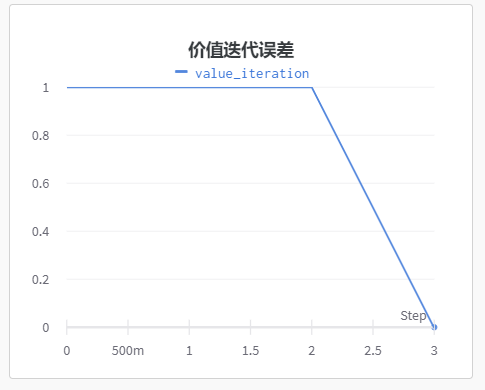
而价值迭代曲线如下:
分析可知,在首次策略评估中,由于初始化的是随机等概率策略,故评估误差的收敛十分缓慢,而在收敛后执行策略提升后得到了较优解,策略将朝着最优解迅速收敛。
反观价值迭代误差曲线,在前三次迭代中,状态价值函数的变化量都是1,这意味着每次迭代中至少有一个状态的价值发生了显著变化(靠近目标点的状态)。最后一次迭代中,状态价值函数的变化量为0,表示算法已经收敛到最优解。