一、红黑树泛型实现map，set

struct RBTreeNode
{
	RBTreeNode<K,V>*_left;
	RBTreeNode<K,V>*_right;
	RBTreeNode<K,V>*_parent;
	T _data;//int pair<K,V>
	Color _col;
	RBTreeNode(const T&data)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_data(data)
	{}
};
template<class K,class T,class KeyOfT>
//本来要T就足够了，但是Find需要使用K，所以这个参数模板K用于专用于Find
class RBTree
{
	typedef RBTreeNode<T> Node;
private:
	Node*root;
}

模板参数的第一个专用于Find，下面细说

template<class K,class V>
class map
{
	struct MapKeyOfT
	{
		const K& operator()(const pair<K,V>&kv)
		{
			return kv.first;
		}	
	}
private:
	RBTree<K,pair<K,V>，MapKeyOfT> _t;
}

template<class K>
class set
{
	struct SetKeyOfT
	{
		const K& operator()(const K&key)
		{
			return key;
		}	
	}
private:
	RBTree<K,K,SetKeyOfT> _t;
}

map和set只是薄薄的一层封装，真正还是红黑树实现的，这颗红黑树的DataType，你传什么我就是什么，我拿一个T来接收这个类型
在这里插入图片描述

对多出来的模板参数的解释

①****首先我们只需要给红黑树传T就行了，不然的话一个红黑树就需要实现两次，分别是K的树和pair<K,V>的树，因为有两个模板参数

②****其次我们既然有一个T就行了，那我们又在前面传一个K过去干嘛？其实在其他地方好像确实用不着，但是注意find的时候，我们都是通过键值查找的，不可能说T _t; 我通过_t.first来查找它的value吧，那这个结点的类型你知道是pair<K,V>还是K呢？所以我们需要单独的传K来解决find这个问题

③红黑树其实是有比较的，因为红黑树是一颗搜索二叉树，那么中序遍历就是一个有序序列，所以我们在插入结点的时候就需要通过比较来确定插入结点的位置，所以这时候又要多一个KeyOfT的一个参数，因为和②相同，我们不确定结点的类型，不能通过_t.first来比较。另外呢KeyOfT就是一个仿函数，我们实现红黑树的时候就可以KeyOfT(cur->_data)来对结点的类型进行处理。

可以看到，STL源码中也是通过该种方式进行处理的
在这里插入图片描述

二、map和set对红黑树迭代器的封装

template<K,V>
class Map
{
	typedef typename RBTree<K,pair<K,V>,MapKeyOfT>::iterator iterator;
	//typedef，加上typename的原因是区分这里的迭代器和静态成员变量
	//因为静态成员变量也是这样调用的，编译器分不清
	iterator begin()
	{
		_t.begin();
	}
	iterator end()
	{
		_t.end();
	}
};//复用红黑树的操作

①迭代器operator++

这里就需要非递归的思路，但是并不能直接用栈去模拟，因为直接用栈的话太大了，我们可以放一个结点的指针
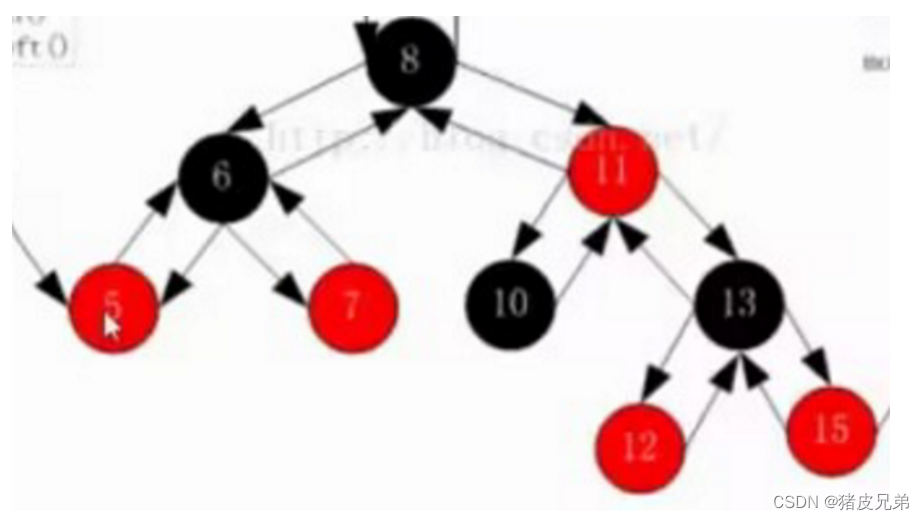
在这里插入图片描述

如果右子树不为空：那么找右子树中序遍历的第一个结点(也就是右子树最左结点)
如果右子树为空：
①如果该结点是左结点，那么找父亲
②如果该结点是右结点，那么找父亲的父亲，直到找到某个结点是左孩子(因为右孩子的父亲都被访问过，这里需要对二叉树的非递归非常了解)

/*模板*/Self&operator++()
{
	if(_node->_right)//有右孩子，找右孩子中序遍历 第一
	{
		Node*left = _node->_right;
		while(left -> _left)
		{
			left=left->_left;	
		}
		_node = left;
	}
	else
	{
		Node*parent=_node->_parent;
		Node*cur = _node;
		while(parent!=nullptr && ncur==parent->_right)
		{
			cur = cur->parent
			parent=parent->_parent;
			//直到为左节点或者为根
		}
		_node=parent;
		//返回父节点
	}
	return *this;
}

②operator–

在这里插入图片描述
5 6 7 8 10 11 12 13 15
15 13 12 11 10 8 7 6 5
和++完全反过来即可

Self&operator--()
{
	if(_node->_left)
	//有左孩子，访问左子树反向中序的第一个，也就是最右
	{
		Node*right = _node->_left;
		while(right->_right)
		{
			right = right->_right;
		}	
		_node=right;
	}		
	else
	//右孩子，访问父节点
	//左孩子，继续往上，直到是右孩子，或者是根，返回父亲
	{
		Node*parent=_node->_parent;
		Node*cur = _node;
		while(parent!=nullpre&&cur==parent->_left)
		{
			cur=cur->_parent;
			parent=parent->_parent;
		}
		_node=parent;
	}
	return *this;
}

但是存在一个问题就是当迭代器是s.end()的时候，相当于it是nullptr，没办法–，所以库中用了其他方法来解决，如下图
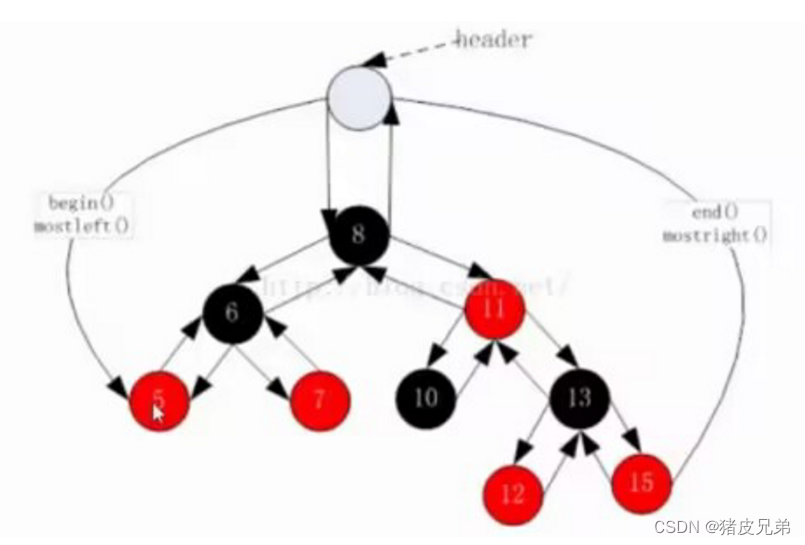
在这里插入图片描述

三、红黑树改装后的insert代码

pair<iterator,bool> Insert(const T&data)
{
	KetOfT kot;//仿函数对象
	if(_root==nullptr)
	{
		_root=new Node(data);
		_root->_col=BLACK;
		return make_pair(iterator(_root)/*iterator类构造*/,true);
	}
	Node*parent=nullptr;
	Node*cur=_root;
	while(cur)//找到插入位置
	{
		if(kot(cur->_data)<kot(data))
		{
			parent=cur;
			cur=cur->_right;
		}
		else if(kot(cur->_data)>kot(data))
		{
			parent=cur;
			cur=cur->left;
		}
		else
		{
			return make_pair(iterator(cur),false);//已存在
		}
	}
	//已找到位置，在此处插入
	cur=new Node(data);
	Node*newnode = cur;//记录返回的迭代器位置
	cur->col=RED;
	//看插在左还是右
	if(kot(parent->_data)<kot(data))
	{
		parent->right=cur;
	}
	else
	{
		parent->_left = cur;
	}
	cur->parent=parent;
	//插入了之后进行平衡已经颜色校正
	//也就是如果不平衡则 红黑树三种处理情况
	while(parent&&parent->_col==RED)//需要处理
	{
		Node*grandfather= parent->_parent;
		assert(grandfather&&grandfather->col==BLACK);
		//存在并且爷爷的col不可能是红
		Node*uncle;//红黑树一切看叔叔
		if(parent==grandfather->_left)
		{
			uncle = grandfather->_right;
			if(uncle&&uncle->_col==RED)
			//情况一，叔叔为红，往上变色即可
			{
				parent->_col = uncle->_col=BLACK;
				grandfather->_col = RED;
				cur=grandfather;
				parent=cur->_parent;
			}	
			else
			//情况二三、叔叔存在且为黑或者不存在，需要翻转
			{
				if(cur==parent->_left)
				//左左，需要一次翻转，然后根据情况图进行变色
				{
					RotateR(grandfather);
					grandfather->_col=RED;
					parent->_col=BLACK;
					//对照翻转后的图改颜色
				}
				else if(cur==parent->_right)
				//左右，单次翻转的话会没有效果，双旋转+变色
				{
					RotateL(parent);
					RotateR(grandfather);
					cur->_col=BLACK;
					grandfather->_col=RED;	
				}
			}	
		}
		else  if(parent==grandfather->_right)
		{
			//差不多的，我就不写了
		}		
	}
	_root->_col=BLACK;
	return make_pair(iterator(newnode),true);
}

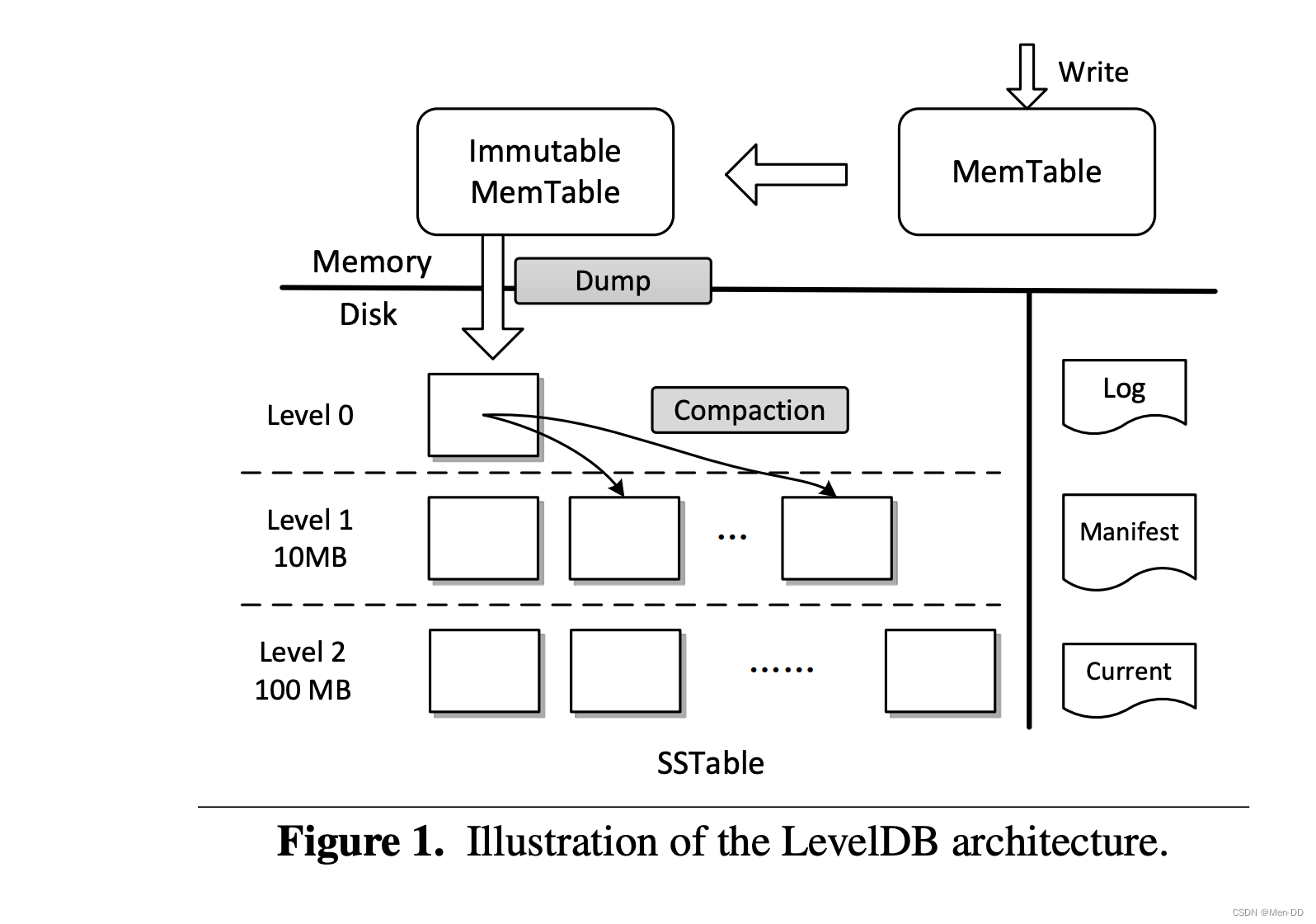
四、红黑树与AVL树比较

红黑树和AVL树都是高效的平衡搜索二叉树，增删查改的时间复杂度都是O(logN),因为最坏查找高度次，红黑树不追求绝对平衡，其次只需要保证最长路径不超过最短路径的二倍(通过颜色的互斥来达到这一点)，这就决定了红黑树会有更少的旋转，所以在经常进行增删的结构中性能比AVL树更优，而且红黑树实现比较简单，所以红黑树的运用比AVL树更多

在这里插入图片描述