#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h> // 添加头文件
#define MAX_VERTEX_NUM 100 //图中最大顶点数
//struct ArcNode* nextarc;
//ArcNode* firstarc;
//这两个是很有必要的,如果你没有这两个指针,你就无法判断当前的顶点是哪一个
// adj是邻接点,firstarc和nextarc分别代表当前和下一个点。
//图的邻接表存储结构定义
typedef struct ArcNode {
int adjvex; //邻接点在数组中的位置下标
struct ArcNode* nextarc; //指向下一个邻接点的指针
} ArcNode;
typedef struct VNode {
char data; //顶点信息
ArcNode* firstarc; //指向第一个邻接点的指针
} VNode, AdjList[MAX_VERTEX_NUM];
//使用结构体嵌套的方式,把两个顶点还有边都给嵌套起来
typedef struct {
AdjList vertices; //邻接表,也就是顶点的意思
int vexnum, arcnum; //顶点数和弧数
bool is_directed; //是否是有向图
} ALGraph;
//查找顶点的第一个邻接点
int FirstAdjVex(ALGraph G, int v)
{
if (G.vertices[v].firstarc != NULL) {
return G.vertices[v].firstarc->adjvex;
}
else {
return -1; //返回“空”
}
}
//查找顶点的下一个邻接点
int NextAdjVex(ALGraph G, int v, int w)
{
ArcNode* p = G.vertices[v].firstarc;
while (p != NULL && p->adjvex != w) {
p = p->nextarc;
}
//先找到w先,题目说相对于w的下一个邻接点
if (p != NULL && p->nextarc != NULL) {
return p->nextarc->adjvex;
}
else {
return -1; //返回“空”
}
}
//v是图中的某个顶点也就是 ArcNode* p,即G.vertices[v].firstarc;
//而p->adjvex != w这是v当前的邻接点
//那下一个邻接点自然就是 p->nextarc->adjvex了
//一般节点的下一个节点就只有一个,
// 不是DFS不会一直往下面找,下一个就到空了,所以说是合理的循环。
//题目的意思就是说,w是v的临接节点。
//插入一个新顶点
void InsertVex(ALGraph* G, char v)
{
if (G->vexnum >= MAX_VERTEX_NUM) {
printf("Error: The graph is full!\n");
return;
}
G->vertices[G->vexnum].data = v;//存放点
G->vertices[G->vexnum].firstarc = NULL;//存放其邻接点
G->vexnum++;
}
//删除一个顶点及其相关的弧
void DeleteVex(ALGraph* G, char v)
{
int i, j;
ArcNode* p, * q;
i = LocateVex(*G, v);//找到顶点位置
if (i == -1) {
printf("Error: Vertex not found!\n");
return;
}
//删除与该顶点相关的弧
for (j = 0; j < G->vexnum; j++) {
p = G->vertices[j].firstarc;//寻找每个图中的所有的第一个邻接点。
while (p != NULL) {
if (p->adjvex == i) {
//如果邻接点是该下标的点
q = p->nextarc;
//因为是第一个邻接点,不存在有无前后的问题,所以直接接上下面一段就行了
free(p);
G->arcnum--;
p = q;
}
else {
//指针要动的只是邻接点为i的点
//在它后面的点,直接下标往前移一位就行了
if (p->adjvex > i) {
p->adjvex--;
//就是已经明确,我们要删除i点,
// 那么其他所有的邻接点下标位置都要往前移1位
//因为要删除i点了,那么所有的点的位置都要发生变化,就像数组那样
//删除一个元素,全部元素都要往前移动。
//至于前面的 if (p->adjvex == i)
//那是因为直接将p点直接删除了,自然就不需要再管它的位置在哪里了
}
p = p->nextarc;//继续往下找,重复当前操作。
}
// 在这段代码中,adjvex属性表示一个弧所指向的顶点在图中的索引位置。
// 当删除与指定顶点相关的弧时,如果不进行调整,
// 那些位于指定顶点之后的顶点索引将会发生变化。
//通过将p指向的弧的adjvex属性减1,可以确保顶点之间的编号连续性。
// 也就是说,删除一个顶点之后,
// 它之后的顶点的索引都需要减少1,以保持对应关系的正确性。
//
// 例如,假设原来顶点i之后的顶点分别为i + 1、i + 2、i + 3,
// 删除与顶点i相关的弧之后,i + 1变成了i,i + 2变成了i + 1,i + 3变成了i + 2,以此类推。
// 这样做的目的是为了在删除操作之后,
// 依然可以通过顶点的索引来正确访问和操作图的邻接信息。
}
}
//删除该顶点本身
//弧跟顶点是不一样的概念
for (j = i + 1; j < G->vexnum; j++) {
G->vertices[j - 1] = G->vertices[j];
}
for (j = 0; j < G->vexnum; j++) {
p = G->vertices[j].firstarc;
while (p != NULL) {
if (p->adjvex > i) {
p->adjvex--;
}
p = p->nextarc;
}
}
G->vexnum--;
// 第一次循环是在删除与指定顶点相关的弧时进行的。
//当找到邻接点的索引大于被删除顶点的索引时,将其减1,以保持顶点之间的编号连续性。
// 第二次循环是在删除顶点本身后进行的。对于每个顶点,
// 遍历其邻接链表,如果邻接点的索引大于被删除顶点的索引,
// 则将其减1,同样是为了保持邻接信息的正确性。
// 这两次循环的目的都是使得删除一个顶点后,
// 其他顶点的索引发生相应变化,以确保后续的访问和操作仍然有效。
}
//邻接表表示当前顶点中
//分支到的任何一个下一个的顶点。
//
//而每一次都指针指向下一个然后删除原先的p节点。
//也就等于断开了所有与当前节点的链接,
//也就成功消除了它的所有弧了。
//插入一条新弧
void InsertArc(ALGraph* G, char v, char w)
{
int i, j;
ArcNode* p, * q;
i = LocateVex(*G, v);
j = LocateVex(*G, w);
if (i == -1 || j == -1) {
printf("Error: Vertex not found!\n");
return;
}
p = (ArcNode*)malloc(sizeof(ArcNode));
p->adjvex = j;//邻接点是j
p->nextarc = G->vertices[i].firstarc;//因为是插入,所以用next而非first
G->vertices[i].firstarc = p;
//p代替了 G->vertices[i].firstarc
//就是因为p中还有adj这个j的值,
/*就是为了插入新弧才代替 G->vertices[i].firstarc的*/
//所以说原地址的 G->vertices[i].firstarc把它换成p就成功插入了。
//p是新的头结点,所以原来的地址改成p的指针没毛病
/* 首先,p->nextarc = G->vertices[i].firstarc;
将p的下一个指针指向顶点i的原第一个邻接边,这样p就成为了新的第一个邻接边。
然后,G->vertices[i].firstarc = p;
将顶点i的第一个邻接边指针指向p,即p成为了顶点i邻接表的新的第一个节点。*/
/* 又忘了指针偏移了,你记住,变动链表以后一定要把指针的头指向新的头结点,不然全部都错了!*/
G->arcnum++;
if (!G->is_directed) {
q = (ArcNode*)malloc(sizeof(ArcNode));
q->adjvex = i;
q->nextarc = G->vertices[j].firstarc;
G->vertices[j].firstarc = q;
G->arcnum++;
}
}
//p->adjvex 放置末端的点
//G->vertices[i].firstarc; 放置前端的点
//问:p->nextarc = G->vertices[i].firstarc; 为什么不直接写成p = G->vertices[i].firstarc;?
//这是因为G->vertices[i].firstarc是一个指向边表结构体的指针,
//而p是一个指向边表结构体的指针变量。
//如果将两者直接赋值,会导致p与G->vertices[i].firstarc指向同一块内存区域,
//任何一方对该内存区域的修改都会影响另一方。这可能不是我们期望的结果。
//
//正确的做法是让p指向与G->vertices[i].firstarc相同的内存地址,
//但是它们是两个不同的指针变量,互相独立,对其中一个指针变量的修改不会影响另一个。
//所以应该写成p->nextarc = G->vertices[i].firstarc,
//这样可以保证p指向与G->vertices[i].firstarc相同的内存地址,
//但是它们是两个不同的指针变量,互相独立,对其中一个指针变量的修改不会影响另一个。
//总结:指针的特殊性问题,直接赋值就表示指向同一个地点,p指针就等于所指向的目标的地址。
//不独立,修改p也就等于修改了原地址的值。所以必须要用next才能成为独立的指针。
//相当于我只是使用了原地址的值,但我是作为独立的一个变量
//删除一条弧
void DeleteArc(ALGraph* G, char v, char w)
{
int i, j;
ArcNode* p, * q;
i = LocateVex(*G, v);
j = LocateVex(*G, w);
if (i == -1 || j == -1) {
printf("Error: Vertex not found!\n");
return;
}
p = G->vertices[i].firstarc;//从起点开始找
q = NULL;
while (p != NULL && p->adjvex != j) {
q = p;
//为什么要保存前面的顶点?
//为了储存前面表的数据,方便后面衔接。
p = p->nextarc;
}
if (p != NULL) {
if (q == NULL) {
G->vertices[i].firstarc = p->nextarc;
//只有一个点的情况
}
else {
q->nextarc = p->nextarc;
}
free(p);
G->arcnum--;
}
if (!G->is_directed) {
p = G->vertices[j].firstarc;
q = NULL;
while (p != NULL && p->adjvex != i) {
q = p;
p = p->nextarc;
}
if (p != NULL) {
if (q == NULL) {
G->vertices[j].firstarc = p->nextarc;
}
else {
q->nextarc = p->nextarc;
}
free(p);
G->arcnum--;
}
}
}
//定位某个顶点的位置
int LocateVex(ALGraph G, char v)
{
int i;
for (i = 0; i < G.vexnum; i++) {
if (G.vertices[i].data == v) {
return i;
}
}
return -1; //未找到
}
int main()
{
ALGraph G;
G.is_directed = false; // 设置图为无向图
G.vexnum = 0;
G.arcnum = 0;
InsertVex(&G, 'A');
InsertVex(&G, 'B');
InsertVex(&G, 'C');
InsertVex(&G, 'D');
InsertArc(&G, 'A', 'B');
InsertArc(&G, 'A', 'C');
InsertArc(&G, 'B', 'D');
InsertArc(&G, 'C', 'D');
printf("The first adjacent vertex of A is %c\n", G.vertices[0].firstarc->adjvex + 'A');
printf("The next adjacent vertex of A after B is %c\n", NextAdjVex(G, 0, LocateVex(G, 'B')) + 'A');
DeleteArc(&G, 'B', 'D');
DeleteVex(&G, 'C');
return 0;
}


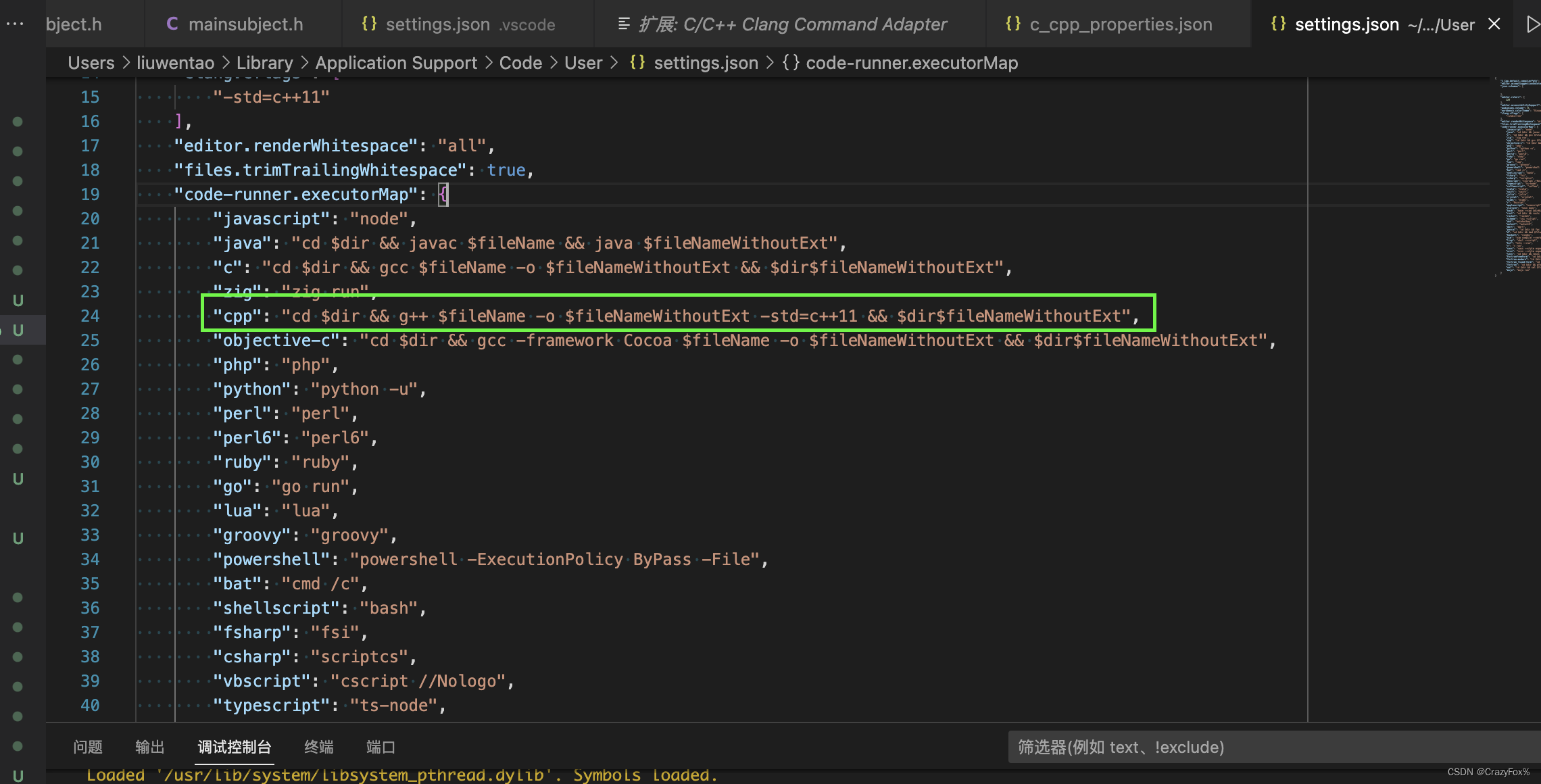
![[环境配置]vscode免密ssh的设置流程](https://img-blog.csdnimg.cn/b62bbbf087a9490f969d930e46ba6082.png)