目录

棋盘问题

leetcode51题.N皇后

---

对回溯算法感兴趣的朋友也可以多多支持一下我的其他文章。

回溯算法详解-CSDN博客

经典的回溯算法题leetcode组合问题整理及思路代码详解-CSDN博客

经典的回溯算法题leetcode子集问题思路代码详解-CSDN博客

经典的回溯算法题leetcode全排列问题思路代码详解-CSDN博客 

棋盘问题

一般棋盘问题都是用回溯算法来做的，我们之前说过回溯算法是一种暴力方法尝试每一种可能，思路不难但是写起来很容易出错。

leetcode51题.N皇后

51. N 皇后 - 力扣（LeetCode）

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的n 皇后问题的解决方案。

每一种解法包含一个不同的n皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

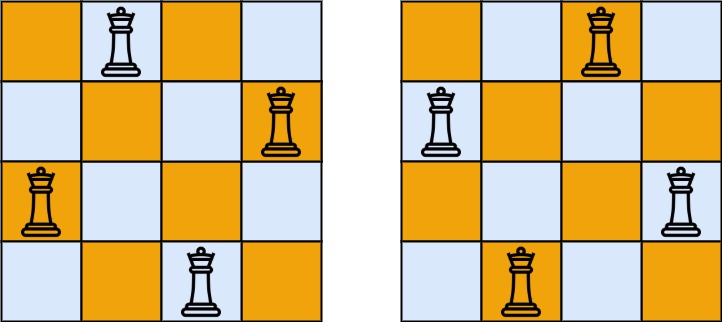
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

class Solution { 
    //存放结果集的变量res
    List<List<String>> res = new ArrayList<>();
    public List<List<String>> solveNQueens(int n) {
        char[][] map = new char[n][n];
      //初始化
        for(int i = 0;i < n; i++){
            for(int j = 0; j < n; j++){
                map[i][j] = '.';
            }
        }
        backTrack(map, 0, n);
        return res;
    }

    //回溯函数：参数有棋盘（二维字符类型）、处理到了第几行、一共有几行
    void backTrack(char[][] map, int row, int n){
        // 结束条件：处理到最后一行
        if(row == n){
            res.add(help(map, n));
            return;
        }

        // 递归+回溯
        for(int col = 0; col < n; col++){
            // 判断能否存放皇后
            if(isValid(map, row, col, n)){
                map[row][col] = 'Q';
                backTrack(map, row+1, n);
                map[row][col] = '.';
            }
        }
    }

    boolean isValid(char[][] map, int row, int col, int n){
        // 判断列
        for(int i = 0; i < row; i++){
            if(map[i][col] == 'Q'){
                return false;
            }
        }
        // 判断右斜
        for(int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--){
            if(map[i][j] == 'Q'){
                return false;
            }
        }

        // 判断左斜
        for(int i = row - 1, j = col + 1; i >=0 && j < n; i--, j++){
            if(map[i][j] == 'Q'){
                return false;
            }
        }

        return true;
    }

    // 把二位字符数组转为List<String>
    List<String> help(char[][] map, int n){
        List<String> temp = new ArrayList<>();
        for(int i = 0; i < n; i++){
            StringBuilder build = new StringBuilder();
            for(int j = 0; j < n; j++){
                build.append(map[i][j]);
            }
            temp.add(build.toString());
        }
        return temp;
    }
}