2022年MathorCup高校数学建模挑战赛—大数据竞赛

A题 58到家家政服务订单分配问题

原题再现：

  “58 到家”是“58 同城”旗下高品质、高效率的上门家政服务平台，平台向用户提供家政保洁、保姆、月嫂、搬家、维修等众多生活领域的服务。在家政保洁场景中，用户在平台下单购买服务后，平台会将订单分配给一个保洁阿姨，阿姨接到订单后按照用户指定的服务时间上门，进行保洁服务。平台在将订单分配给一个保洁阿姨时，一方面，为了提高对顾客的服务质量，需要尽量分配服务分较高的阿姨，其中阿姨的服务分是基于阿姨历史订单的评价情况得到，取值为[0,1]，值越大越好；另一方面，为了帮助阿姨提高接单量，需要尽量缩短阿姨相邻单之间的通行时间。
  每天通过平台进行分配的订单量是巨大的，当前平台实现了一套订单分配算法，本问题研究的是如何优化系统的分配算法，提高算法的求解能力，实现提升顾客体验、节省阿姨时间。
  数据说明：
  数据包含一天内、一个区域的所有订单和所有保洁阿姨。


  约束条件及假设：
  1. 所有订单都要分配一个且只有一个阿姨；
  2. 每个订单需要指定一个服务开始时间，这个时间的取值范围为 [最早时间，最晚时间]，且是半点的整数倍；
  3. 一个阿姨同时只能服务一个订单；
  4. 阿姨需要在每个订单的服务开始时间之前到达客户位置；
  5. 阿姨每天开始任务时必须从初始点位置出发；
  6. 任意两点的距离为欧式距离；
  7. 保洁阿姨的行驶速度为 15 千米/小时。 优化目标：
  将每个订单匹配阿姨时，优化的目标是：
  1. 所有订单匹配的阿姨的服务分，其平均值 A 尽可能大；
  2. 最小化每单的平均通行距离 B。一个订单的通行距离指的是阿姨从上一个地点到本单地点的距离（欧式距离），其中阿姨第一个订单的通行距离等于从初始点到第一个订单位置的距离，单位是千米；
  3. 最小化阿姨服务订单的平均间隔时间 C。一个订单的间隔时间指的是，阿姨从上一个单服务结束时刻到本单服务开始时刻的时间间隔，单位是小时，其中阿姨第一个订单的间隔时间设定为 0.5 小时（阿姨首单需要做基本的准备工作，不考虑阿姨从初始点到第一个订单的通行时间）；
  4. 总体目标是各个目标的加权和：αA-βB-γC，其中α=0.78、β=0.025、γ=0.195，得分四舍五入取 6 位小数。目标值越大越好。
  初赛问题
  问题 1：只考虑离线批量派单模式。附件 1 与附件 2 中分别给出的是一天的所有订单信息与阿姨信息。
  (a) 请设计最优的订单与阿姨匹配算法，将所有订单进行分配，并将求解结果填写到 result1.txt 中。（订单必须全部分配、阿姨不需要全部匹配订单）。
  (b) 基于(a)的算法，请对附件 1 中的前 50 个订单与附件 2 中前 20 个阿姨，重新运行算法，给出阿姨的执行任务列表，并画出阿姨的行动轨迹图。

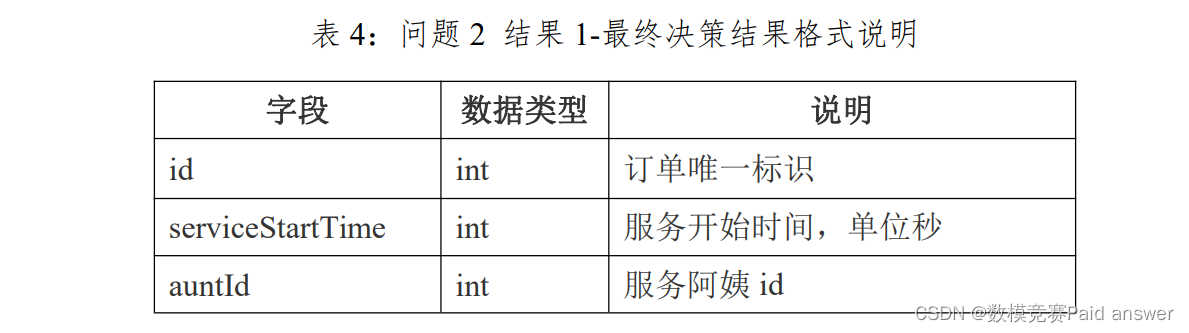
  问题 2：线上批量派单模式。在实际业务场景中，通常采用固定的频率派单，每 30 分钟将该段时间内产生的新订单统一分配；分配时允许部分订单暂时不派单，称之为压单，但是压单订单必须满足服务开始时间的最早时 间 比 当 前 时 间 晚 于 2 个 小 时 （ 不 包 括 2 个 小 时 ） 也 即 满足：serviceFirstTime-currentTime>2h；请设计这种情况下的每批订单的最优分配算法。并将求解结果 1-最终决策结果填写到 result21.txt 中，结果 2-每次决策结果填写到 result22.txt 中。

整体求解过程概述(摘要)

  随着我国经济水平的发展和人民生活质量的提高，人们对家政服务的要求日益专业化、规范化、综合化，为增强客户体验及提高时间效率，探究家政服务公司订单分派系统的优化问题，我们通过贪心算法的思想，设计基于收益评估的阿姨与订单分配算法，来研究如何在离线批量派单时达到收益最大，接着引入下单时间对模型进行改进，建立多批次的分配模型，实现订单的多批次分配。
  针对问题一，首先根据题意定义决策变量，并将题中所给的约束条件、优化目标等转化为具体的数学规划模型。然后因为是离线派单模式，因此所有订单的信息都是已知的，考虑到问题的规模较大，我们根据数学规划模型设计基于收益评估的阿姨与订单分配算法。该算法首先通过贪心算法定义每个订单的服务优先级，然后将订单按照客户要求的最晚服务时间进行升序排序，若是最晚服务时间相同则按照优先级进行降序；再给每一个订单进行每个阿姨的预分配，依据贪心算法预测出每个符合条件的阿姨在分配给该订单的情况下的收益，然后根据具体的收益情况进行阿姨分配。最终通过上述算法建立基于收益评估的阿姨与订单分配模型，决策出各个订单的分派方案,并绘制所有订单分配最大收益的频数直方图和阿姨分派次数的统计图对结果进行可视化，发现最大收益集中分布在区间 [0.55,0.65] 上，且阿姨的重复分配率高，绝大部分阿姨未被分配，高达2110个，最终计算出该算法下的最优总体目标为0.611404。接着我们针对前50个订单与前20个阿姨进行分派，并计算出该数据集下的总体目标为0.477170，并绘制出分派过的阿姨的行动轨迹图。
  针对问题二，根据题意需要考虑下单时间这一因素，根据固定的频率将订单根据下单时间进行分批，每次只能在已知当前批次订单和被压单订单的情况下进行最优的阿姨分派。因此我们对问题一的模型进行改进，设计基于收益评估的多批次阿姨与订单分配模型。主要原理是组建当前批次订单并对当前批次订单进行阿姨预分配的收益预测，然后选出当前收益最大的分配情况和压单情况，再对下一批订单进行分配。因为在优先级机制的保障下，最先分配阿姨的订单一定是时间上较为紧急的订单，因此在处理后面几个订单时，如果符合压单且预分配收益小于事先定义的阈值，则对其进行压单。我们对阈值进行参数寻优，从而确定最优阈值为 0.67，接着通过上述模型决策出问题二各批次订单的分配结果和每次决策结果，并绘制所有订单分配最大收益的频数直方图和阿姨分派次数的统计图对结果进行可视化，发现问题二的直方图集中数据区间与问题一相似，但未被分派的阿姨数量减少，最终计算出该方案下的最优总体目标为 0.612838，总压单次数为 5494 次。
  最后我们编写 C++代码对模型进行检验，发现问题一和问题二的订单分派结果均通过检验，说明不存在一个阿姨同时服务多个订单或订单漏分配的情况，订单分派合理。

模型假设：

  1) 假设顾客不会随意取消订单。
  依据：当前订单的取消可能会导致需要对后续订单进行重新分配才能保证最优目标。
  2) 假设阿姨体力充足，无订单服务次数限制。
  依据：阿姨存在一天服务多个订单的情况。
  3) 假设阿姨每次通行和服务时无突发情况。
  依据：意外的发生会影响该阿姨后续订单的分派。

问题分析：

  数据的预处理分析
  首先通过程序检测各个文件，发现各文件都不存在缺失值。然后通过编写 C++ 代码，将订单信息的时间戳转换为具体日期，发现所有订单中的服务时间都在一天内，为2022 年 9 月 10 日当天的 8:00 至 22:00，因此只需针对当天进行订单分派工作。
  问题一的分析
  针对问题一，首先根据题意定义决策变量，并将题中所给的约束条件、优化目标等转化为具体的数学规划模型。然后因为是离线派单模式，因此所有订单的信息都是已知的，考虑到问题的规模较大，我们设计基于收益评估的阿姨与订单分配算法：首先通过贪心算法3定义每个订单的服务优先级，将订单按照客户要求的最晚服务时间进行升序排序，若是最晚服务时间相同则按照优先级进行降序；再给每一个订单进行阿姨的预分配，预测出每个符合条件的阿姨分配给该订单的收益，然后根据收益情况进行具体的阿姨分配。最终通过上述算法建立基于收益评估的阿姨与订单分配模型，并给出问题一的计算结果和绘制前 50 个订单与前 20 个阿姨的行动轨迹图。
  问题二的分析
  针对问题二，根据题意我们需要引入下单时间这一因素，根据固定的频率将订单根据下单时间进行分批，每次只能在已知当前批次订单的情况下进行最优的阿姨分派。因此我们对问题一的模型进行进一步加工，将其设计成基于收益评估的多批次阿姨与订单分配模型，实现订单的在线调度4。次进行订单收益对当前批次订单进行阿姨预分配的收益预测，然后选出当前最高收益5的分配情况，再对下一批订单进行分配。针对符合压单情况的订单，因为我们在优先级的保障下，最先分配阿姨的订单一定是时间上较为紧急的订单，因此在处理后面几个订单的适合，如果符合压单且预分配收益小于阈值，则对其进行压单。最终我们通过上述模型计算出问题二的最终决策结果和每次决策结果。

模型的建立与求解整体论文缩略图

全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：

程序如下:

#include <iostream>
#include <algorithm>
#include <string>
#include <vector>
#include <stack>
#include <queue>
using namespace std;


void backTrack(vector<vector<double>>& num,vector<bool>&used, vector<int>& pre,
 vector<int>& cur,double curProfit, double&preProfit, int n, int pos)
{
	//如果pos == n 说明行数已经达到n行，所有的行都已经选完，是一种结果
	if (pos == n) 
	{
		//全局找最大，判断是否出现更优解
		if (curProfit > preProfit)  
		{
			//更新当前最大的和
			preProfit = curProfit;
			//数组赋值,将这个最优解的数组赋值给pre，最后用来输出
			pre = cur; 
		}
		return;
	}
	
	//枚举第pos行的每一列
	for (int i = 0; i < n; i++)
	{
		//改行必须在之前没有被选择使用过，必须满足题意
		if (!used[i])  // 标记第 i列，下一次第i列就不能选择了
		{
			//代表本次选择pos行的i列元素，进行标记本次递归的选择位置
			//因为可能出现本次选择是最优的情况，所以需要保存
			cur[pos] = i;  // 记录每一个 pos行对应的列数i，下面的就是回溯过程
			
			//代表当前的评分和加上本次的选择
			//同理和cur一样都要保存
			curProfit += num[pos][i];
			
			//代表着第i例被使用过，下次不能在选择第i列
			used[i] = true;
			backTrack(num,used,pre,cur, curProfit, preProfit, n, pos + 1);
			//撤销选择
			curProfit -= num[pos][i];
			//撤销标记
			used[i] = false;
		}
	}
}

int main()
{
	int n;
    while (cin >> n)
	{
		vector<vector<double>> vvd(n, vector<double>(n));
		for (int i = 0; i < n; i++)
		{
			for (int j = 0; j < n; j++)
			{
				cin >> vvd[i][j];
			}
		}
		
		vector<int> pre(n); //  记录最优解的每个值 所在的 列数
		vector<int> cur(n); //  列数加入数组
		vector<bool> used(n); // 标记数组， 因为一列只能选择一个
		double preProfit = INT_MIN; // 全局的最大值
		double curProfit = 0.0; // 当前的最大值
		int pos = 0;  // pos就是行数，pos到达一行，就选y值就可以了
		backTrack(vvd, used, pre, cur, curProfit, preProfit, n, pos); 

		//打印结果
		printf("%4.2f\n",preProfit);
		//cout << preProfit << endl;
		for (int i = 0; i < pre.size(); i++)
		{
			cout << i + 1 << " " << pre[i] + 1 << endl;
		}
	}
}

全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可