五、动态规划
基本概念
阶段(Stage):将所给问题的过程,按时间或空间特征分解成若干相互联系的阶段,以便按次序去求解每阶段的解,常用字母 k k k 表示。
状态(State):各阶段开始时的客观条件叫做状态。描述各阶段状态的变量称为状态变量,常用 s k s_k sk 表示第 k k k 阶段的状态变量,状态变量 s k s_k sk 的取值集合称为状态集合,用 S k S_k Sk 表示。状态变量应具有无后效性:某阶段状态给定后,这个阶段以后过程的发展不受这段以前各状态的影响。
决策和策略(Decision and Policy):各阶段状态确定后,就可以作不同的决定,从而确定下一阶段的状态,这种决定称为决策。表示决策的变量称为决策变量,常用 u k ( s k ) u_k(s_k) uk(sk) 表示,允许的决策集合常用 D k ( s k ) D_k(s_k) Dk(sk) 表示。各阶段决策确定后,整个问题的决策序列就构成一个策略。
状态转移方程:如果给定了第 k k k 阶段的状态 s k s_k sk ,本阶段决策为 u k ( s k ) u_k(s_k) uk(sk) ,则第 k + 1 k+1 k+1 阶段的状态 s k + 1 s_{k+1} sk+1 也就完全确定,它们的关系就称为状态转移方程。
指标函数:用于衡量所选定策略优劣的数量指标称为指标函数。直接指标函数表示某阶段的决策产生的效益,常用 d k ( u k ) d_k(u_k) dk(uk) 表示。最优指标函数表示从第 k k k 阶段状态为 s k s_k sk 采用最优策略时,后部过程的最优收益值,常用 f k ( s k ) f_k(s_k) fk(sk) 表示。
五要素
动态规划模型五要素:
- 将问题按时空特征恰当地划分为若干个阶段。
- 正确地规定状态变量 s k s_k sk ,使得它既能描述过程的演变,又具有无后效性。
- 正确地规定决策变量 u k u_k uk 以及每阶段的允许决策集合 D k ( s k ) D_k(s_k) Dk(sk) .
- 正确写出状态转移方程 s k + 1 = g k ( s k , u k ) s_{k+1}=g_k(s_k,u_k) sk+1=gk(sk,uk) 。
- 正确地定义各阶段的直接指标函数 d k ( s k , u k ) d_k(s_k,u_k) dk(sk,uk) 和后部子过程的最优指标函数 f k ( s k ) f_k(s_k) fk(sk) ,并写出基本方程(以 max \max max 和相加求收益为例): { f k ( s k ) = max { d k ( s k , u k ) + f k + 1 ( s k + 1 ) } , k = n , n − 1 , ⋯ , 1 f n + 1 ( s n + 1 ) = 0 , 边界条件 \begin{cases} f_k(s_k)=\max\{d_k(s_k,u_k)+f_{k+1}(s_{k+1})\} &,k=n,n-1,\cdots,1 \\ f_{n+1}(s_{n+1})=0&,边界条件\end{cases} {fk(sk)=max{dk(sk,uk)+fk+1(sk+1)}fn+1(sn+1)=0,k=n,n−1,⋯,1,边界条件
生产存储问题
做题时,我们可也按照动态规划模型五要素进行建模,以生产与储存问题为例。
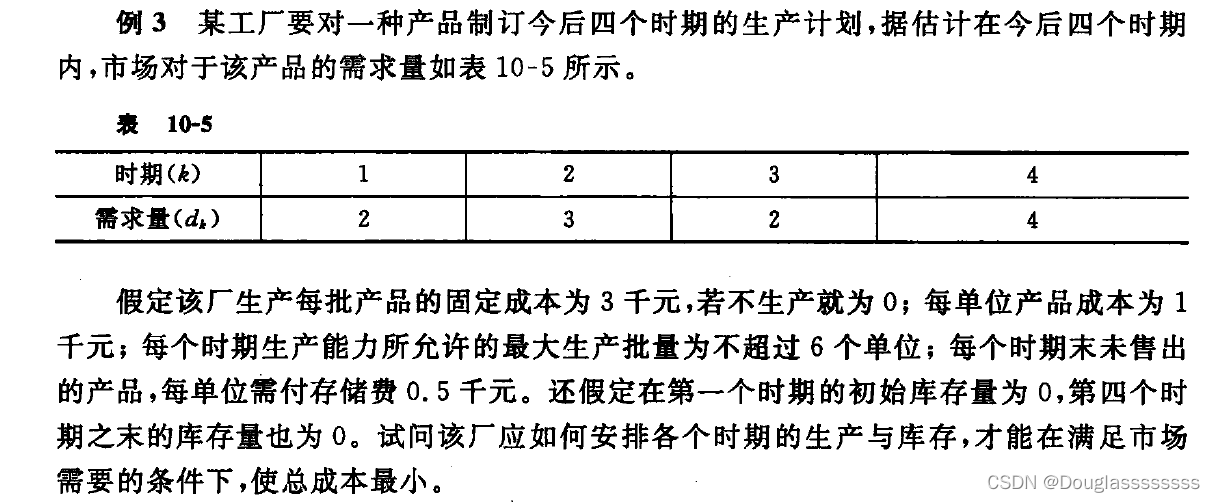
解: 将问题划分为 4 4 4 个阶段( k = 1 , 2 , 3 , 4 k=1,2,3,4 k=1,2,3,4),每个阶段表示一个时期;状态变量 s k s_k sk 表示第 k k k 阶段开始时的库存量;决策变量 x k x_k xk 表示第 k k k 阶段的产品生产量, d k d_k dk 表示第 k k k 阶段的产品需求量,则状态转移方程为: s k + 1 = s k + x k − d k s_{k+1}=s_k+x_k-d_k sk+1=sk+xk−dk 直接指标函数 g k ( x k ) g_k(x_k) gk(xk) 表示第 k k k 阶段决策为 x k x_k xk 时的成本,包括生产成本 c k ( x k ) c_k(x_k) ck(xk) 和存储成本 m k ( x k ) m_k(x_k) mk(xk) 。其中, c k ( x k ) = { 0 , x k = 0 3 + x k , x k = 1 , 2 , ⋯ , 6 ∞ , x k > 6 c_k(x_k)=\begin{cases} 0&,x_k=0\\ 3+x_k&,x_k=1,2,\cdots,6\\ \infty&,x_k>6 \end{cases} ck(xk)=⎩ ⎨ ⎧03+xk∞,xk=0,xk=1,2,⋯,6,xk>6 m k ( x k ) = 0.5 ( s k + x k − d k ) m_k(x_k)=0.5(s_k+x_k-d_k) mk(xk)=0.5(sk+xk−dk) 。最优指标函数 f k ( s k ) f_k(s_k) fk(sk) 表示第 k k k 阶段状态为 s k s_k sk 采用最优策略时,后部过程的最小成本,则递推基本方程为: f k ( s k ) = { min { c k ( x k ) + m k ( x k ) + f k + 1 ( s k + 1 ) } , k = 4 , 3 , 2 , 1 f 5 ( s 5 ) = 0 f_k(s_k)=\begin{cases} \min\{c_k(x_k)+m_k(x_k)+f_{k+1}(s_{k+1})\},k=4,3,2,1\\ f_5(s_5)=0\end{cases} fk(sk)={min{ck(xk)+mk(xk)+fk+1(sk+1)},k=4,3,2,1f5(s5)=0 随后便是每个阶段的求解了,最关键的就是确定 s k s_k sk 和 x k x_k xk 的取值范围,需要瞻前顾后,考虑每阶段的生产能力以及最后阶段的库存要求。
设备更新问题
对于设备更新问题,教材上用了别的符号,让人难以和之前的联系起来,但其实它也可以用我们常见的符号表达的。用一个实际题目来说明。

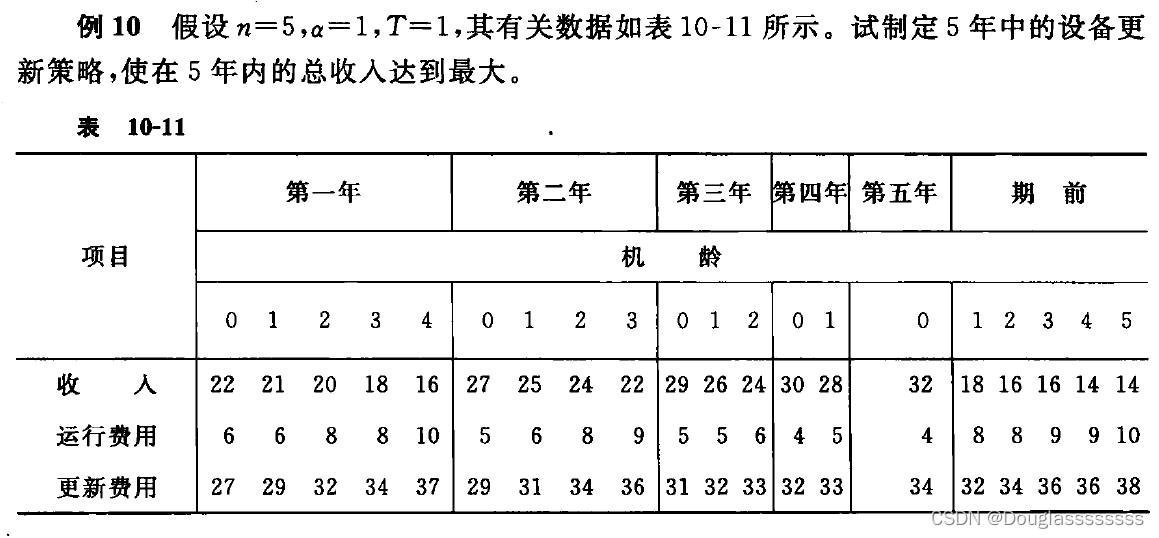
解: 将问题分为 5 个阶段(
k
=
1
,
2
,
3
,
4
,
5
k=1,2,3,4,5
k=1,2,3,4,5),每个阶段代表一年。状态变量
s
k
s_k
sk 表示第
k
k
k 阶段初机器的役龄,决策变量
x
k
x_k
xk 表示第
k
k
k 阶段时保留(K)还是更新(R)。则状态转移方程为:
s
k
+
1
=
{
s
k
+
1
,
x
k
=
K
1
,
x
k
=
R
s_{k+1}=\begin{cases} s_k+1&,x_k=K\\ 1&,x_k=R \end{cases}
sk+1={sk+11,xk=K,xk=R 直接指标函数
g
k
(
x
k
)
g_k(x_k)
gk(xk) 表示第
k
k
k 阶段做出决策
x
k
x_k
xk 的收入,
I
k
(
s
k
)
I_k(s_k)
Ik(sk) 表示第
k
k
k 阶段役龄为
s
k
s_k
sk 的机器带来的收入,
O
k
(
s
k
)
O_k(s_k)
Ok(sk) 表示第
k
k
k 阶段役龄为
s
k
s_k
sk 的机器的运行费用,
C
k
(
s
k
)
C_k(s_k)
Ck(sk) 表示第
k
k
k 阶段役龄为
s
k
s_k
sk 的机器更新费用,则有
g
k
(
x
k
)
=
{
I
k
(
s
k
)
−
O
k
(
s
k
)
,
x
k
=
K
I
k
(
0
)
−
O
k
(
0
)
−
C
k
(
s
k
)
,
x
k
=
R
g_k(x_k)=\begin{cases} I_k(s_k)-O_k(s_k)&,x_k=K\\ I_k(0)-O_k(0)-C_k(s_k)&,x_k=R \end{cases}
gk(xk)={Ik(sk)−Ok(sk)Ik(0)−Ok(0)−Ck(sk),xk=K,xk=R 最优指标函数
f
k
(
s
k
)
f_k(s_k)
fk(sk) 表示第
k
k
k 阶段役龄为
s
k
s_k
sk 的机器采用最优策略时,后部过程的最大收入,可写出递推基本方程为:
f
k
(
s
k
)
=
{
max
{
g
k
(
x
k
)
+
f
k
+
1
(
s
k
+
1
)
}
,
k
=
5
,
4
,
3
,
2
,
1
f
6
(
s
6
)
=
0
f_k(s_k)=\begin{cases} \max\{g_k(x_k)+f_{k+1}(s_{k+1})\},k=5,4,3,2,1\\ f_6(s_6)=0\end{cases}
fk(sk)={max{gk(xk)+fk+1(sk+1)},k=5,4,3,2,1f6(s6)=0 剩下就是根据表中的数据代入递推方程了。
静态规划问题
动态规划方法还可以用来求解一些静态规划问题,如整数规划和非线性规划问题等。一般将约束条件的右端资源量作为状态变量,决策变量为原规划问题的决策变量,直接指标函数为目标函数对应的部分。
有时候最后一个阶段的直接指标函数较为复杂,可以换一换次序,简化计算。





![web:[WUSTCTF2020]朴实无华](https://img-blog.csdnimg.cn/76f178ca69d34e8fb40cc9cd78b76064.png)