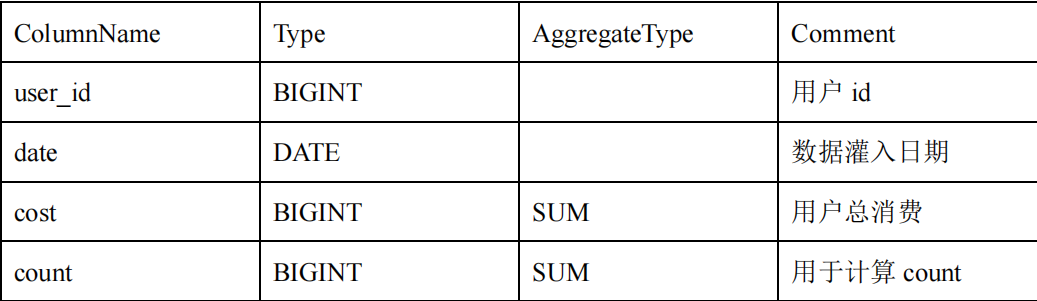
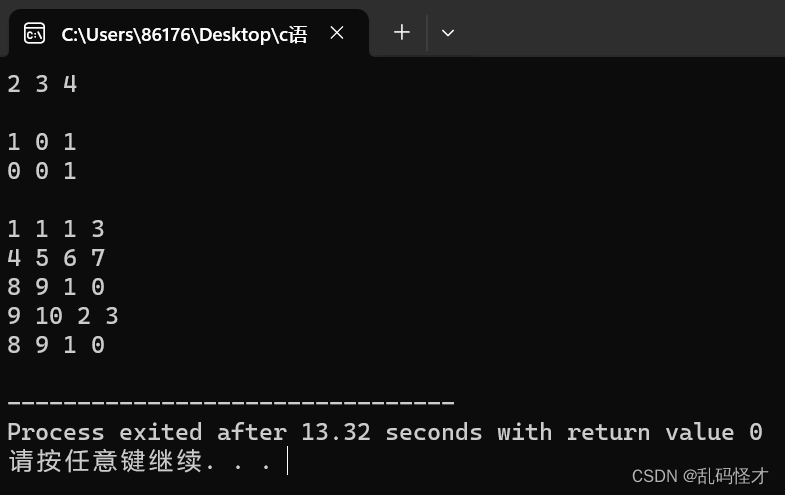
引导
前面几节,我们介绍了有关树的数据结构,我们继续来介绍一种树结构——堆。堆的应用场景有很多,比如从大量数据中找出top n的数据;根据优先级处理网络请求;这些情景都可以使用堆数据结构来实现。
什么是堆?
正如上文所说,堆是一种树结构。它的定义满足以下两点:
- 堆是一个完全二叉树
- 堆中每个节点的值必须大于等于(或小于等于)其子树中每个节点的值
完全二叉树在前面我们已经讲过;第二点,其实等价于堆中每个节点大于等于(或小于等于)其左右子节点。
对于每个节点大于等于左右子节点,我们称为大顶堆;每个节点小于等于左右子节点,我们称为小顶堆。
堆的操作
堆这种数据结构有点不一样。不适合查找或删除指定值的操作。
但是它可以帮助我们解决一些特定的问题。但是不同的问题,都离不开以下核心操作:插入一个元素,删除堆顶元素。
创建一个堆
我们知道完全二叉树适合用数组进行保存。因为它不需要保存左右指针,通过数组下标就可以实现。
数组下表为i的节点,其左子节点的数组下标为2*i,右子节点的数组下标为 2 *i+1;任意节点的父节点下标为i/2;根节点的下标为1.
插入一个元素
向堆中插入一个数据,我们可以将新加入的数据加入到堆的后面,使其继续维持一个完全二叉树。
但是插入一个新的数据就无法保证其父节点大于等于(或小于等于)左右子节点了。于是我们还要进行调整,使其满足堆的特性。我们称为这个过程为堆化。堆化的过程,其实也简单,只要循着插入节点,向上对比,进行交换即可。
| / |
删除堆顶元素
由堆的特性所致,删除堆顶元素,实际上就是找出最大或者最小值的过程。删除堆顶元素其实也简单,可按照以下思路进行:
- 将最后一个元素放到堆顶,保证树是一个完全二叉树
- 从堆顶开始进行堆化,使其满足特质二
| / |
通过插入一个数据和删除堆顶元素的操作流程,我们知道时间的消耗主要集中在堆化中。由于完全二叉树的树高不会超过logn。所以堆的插入数据和删除堆顶元素的时间复杂度都是O(logn)。
如何实现堆排序?
我们已经知道堆的性质以及基本的操作。但是对于一组数据我们该如何进行堆排序呢?原始的数据肯定是无序也不是堆结构的。因此我们第一步应该是建立堆。
建堆
建堆的方式有两种
第一种最简单:首先假设堆中的数据为0,依次将原始数据放到堆中。我们知道插入数据的时间复杂度是O(logn)。故插入第一个数据的消耗的时间为log1,第二个数据消耗的时间为log2...以此推测,第n个数据消耗时间为logn。
方法一消耗的时间为:log1+log2+log3...+logn=O(logn!),并且需要额外的内存。
第二种思路就比较特殊:对于完全二叉树而言,下标从n/2 + 1到n的节点都是叶子节点,并且叶子节点是不需要堆化的。
因此我们只需要将原始数据中下标从1到n/2进行堆化即可,并且不需要额外的内存。
| int buildheap(int heap[],int count) |
那么第二种思路的时间复杂度是多少呢?
我们知道堆化的操作和所在节点的高度有关。由于叶子节点不需要堆化,并且每层节点和节点高度成正比,如图:
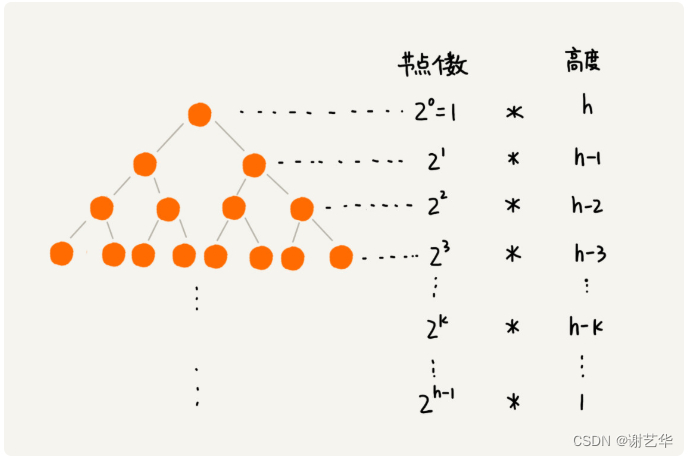
故消耗的时间为:
| T = 2^0 |
由于h=logn(以2为底)通过化简,得出时间复杂度为O(2n-h-2)=O(n)。
至此,我们已将完成建堆
排序
在删除堆顶元素时,我就说过了,这就是排序的过程。因此堆排序,就是将堆顶元素不断删除,直至堆为空。
代码如下:
| int heapsort() |
现在我们看堆排序的时间复杂度是多少?
建堆的时间复杂度是O(n),排序的时间复杂度是O(nlogn)(实际上应该是logn+log(n-1)+log(n-2)+...+log(1),这里方便,我们记录为O(logn))。故堆排序的时间复杂度为O(nlogn)。
快速排序的性能为什么比堆排序的要好?
在排序章节,我们提到了快速排序,它是时间复杂度也是O(nlogn)。但是在实际开发过程中,我们快速排序的性能优于堆排序。我觉得原因有以下几点:
- 堆排序的访问没有快速排序好。即使堆排序也是以数组为存储。但是由于它访问不是连续的,不能很好的利用CPU缓存。
- 对于同样的数据,堆排序的数据交换要多于快速排序。
堆应用
优先级队列
在工作中,我们经常会遇到定时任务的问题。一般思路:将每个任务保存到数组中,每过一个时间间隔(1秒),就检测一下数组,看哪个任务达到了设定时间,如果到达了就取出任务执行,并删除。
其实这样的定时器效率是很低的,为什么呢?
- 往往到达下一个任务之间的间隔是需要很长时间,那么在达到之前所有的检测都是无用的,这是在浪费系统资源
- 如果任务列表的长度很大,那么每次遍历,都会消耗很多的资源。这也是不可取的。
针对该类问题,我们可以采用优先级队列来解决。我们按照任务时间进行堆化。堆顶就是最先要被执行的任务。
修改方案:
- 根据任务时间进行堆化(小堆顶),堆顶任务就是下一个将要被执行的任务
- 计算现在距离下一个任务的时间T,sleep T秒,再执行堆顶任务。这样在执行下一个任务之前,定时器不需要做任何事情,性能大大提高。
Top k
堆在求top k的问题中,表现的也同样出色。
求top K的问题,我们可以先将数据排序,再取前K个元素。我们可以通过快排,那么求top K的时间复杂度是O(nlogn),这同样也很快,难道堆会更好吗?
堆应用的思路:
- 取数据中的前K个元素,建立小顶堆。
- 继续遍历数组中的元素,如果元素大于堆顶元素,则加入堆中,并删除堆顶元素。若比堆顶元素小,则不进行处理。
- 当遍历完整个数组后,堆中的数据就是前top K数据。
假设每个元素都需要进行插入,那么就是堆化n个元素,堆化的时间复杂度是O(logK),故使用过堆求top K的问题,其时间复杂度是O(nlogk)。
求中位数
在求中位数的问题中,我们一般的思路是将原始数据进行排序。
再求中位数,如果n为奇数的话,中位数就是n/2+1;如果n为偶数的话,中位数就是n/2或n/2+1。这种方式的消耗主要集中在对n个数据排序上面,使用快速排序,它的时间复杂度就是O(nlogn)。
但这样的方式比较适合静态数据,当数据能够动态添加时,再采取这样的方式,就不再适合了。
堆对于这种动态数据,求中位数有其优势。我们的思路是这样的:
- 先将现有数据进行升序排序,取前n/2个数据进行大堆顶堆化。后n/2个数据进行小堆顶堆化。(假设n为偶数。若n为奇数,取前n/2+1个数据为大堆顶)
- 当n为偶数时,中位数就是大堆顶和小堆顶的堆顶元素;当n为奇数时,中位数就是大堆顶的堆顶元素;
- 插入一个元素时,如果插入元素小于等于大堆顶元素,我们就将元素插入到大堆顶;反之插入到小堆顶。这样就容易不满足我们的预定:取前n/2个数据进行大堆顶堆化。后n/2个数据进行小堆顶堆化。(假设n为偶数。若n为奇数,取前n/2+1个数据为大堆顶)。我们就需要将两个堆的堆顶元素互相调整,使其满足上诉约定
通过上述的逻辑,我们就可以得到一个适合动态数据,求中位数的方案。其时间复杂度主要集中在堆化过程O(logn)。
总结
本节,我们介绍了堆这种数据结构以及堆结构的定义。也从代码的角度去实现了堆和堆排序。
最后也比较了快速排序相对于堆排序的优点。我后面会继续总结一个关于堆排序的应用方向的一系列题。争取吃透。
![[论文笔记] Scaling Laws for Neural Language Models](https://img-blog.csdnimg.cn/2674d8d5c6c84d59b73491ca58184c91.png)