正交矩阵
定义: 正交矩阵是一种满足
A
T
A
=
E
A^{T}A=E
ATA=E的方阵
正交矩阵具有以下几个重要性质:
- A的逆等于A的转置,即 A − 1 = A T A^{-1}=A^{T} A−1=AT
- **A的行列式的绝对值等于1,即 ∣ d e t ( A ) ∣ = 1 |det(A)|=1 ∣det(A)∣=1
- 正交矩阵的行向量和列向量都是单位正交向量组,也就是说,它们的长度都是 1,而且两两垂直
- 正交矩阵的特征值都是模长为 1 的复数,即它们都在单位圆上。
- 正交矩阵的乘积仍然是正交矩阵,即如果 A 和 B 都是正交矩阵,那么 AB 也是正交矩阵
eg:
[
0
1
0
1
0
0
0
0
1
]
\begin{bmatrix} & 0& 1& 0 & \\ &1& 0& 0 & \\ &0& 0& 1 & \end{bmatrix}
010100001
对角矩阵
定义: 对角矩阵是一种特殊的方阵,它的非对角元素都为零,只有主对角线上的元素可能不为零
性质:
-对角矩阵的逆矩阵等于主对角线上元素的倒数
eg:
[
1
0
0
0
2
0
0
0
3
]
\begin{bmatrix} & 1& 0& 0 & \\ &0& 2& 0 & \\ &0& 0& 3 & \end{bmatrix}
100020003
对称矩阵
定义: 特殊的方阵,它的转置矩阵与自身相等,也就是说,它的元素以主对角线为对称轴对应相等
性质:
- 对称矩阵的特征值都是实数
- 特征向量都是正交的
- 可以通过相似变换对角化
- 其逆矩阵也是对称矩阵
eg:
[
1
2
3
2
2
5
3
5
3
]
\begin{bmatrix} & 1& 2& 3 & \\ &2& 2& 5 & \\ &3& 5& 3 & \end{bmatrix}
123225353
正定矩阵
定义: 给定一个大小为 n × n n \times n n×n的实对称矩阵A,对于任意长度为n的非零向量x,有 X T A x > 0 X^{T}Ax>0 XTAx>0恒成立,则矩阵A是一个正定矩阵
- 其逆矩阵也是对称矩阵

不正定矩阵
定义: 给定一个大小为 n × n n \times n n×n的实对称矩阵A,对于任意长度为n的非零向量x,有 X T A x ≥ 0 X^{T}Ax \ge 0 XTAx≥0恒成立,则矩阵A是一个半正定矩阵
补充知识
单位正交向量组
正交向量组是一组非零的两两正交(即内积为0)的向量构成的向量组
求行列式的绝对值
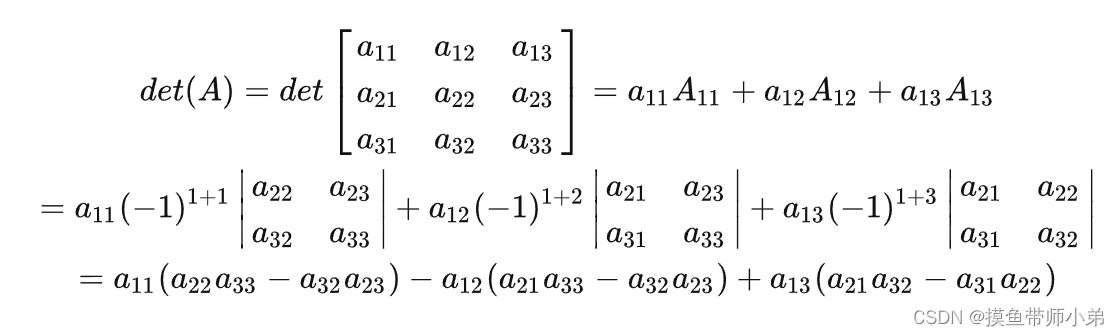






![【Mysql】[Err] 1293 - Incorrect table definition;](https://img-blog.csdnimg.cn/9a52fb68d8424b9387eb1d7c6cef3835.png)