最近在看时间序列的文章,回顾下经典
论文地址
项目地址
Forecasting at Scale
- 摘要
- 1、介绍
- 2、时间业务序列的特点
- 3、Prophet预测模型
- 3.1、趋势模型
- 3.1.1、非线性饱和增长
- 3.1.2、具有变化点的线性趋势
- 3.1.3、自动转换点选择
- 3.1.4、趋势预测的不确定性
摘要
预测是一项常见的数据科学任务,能够帮助组织进行容量规划、目标设定和异常检测。尽管其重要性不言而喻,但在生产可靠且高质量的预测时面临着严峻挑战,特别是当涉及到多样的时间序列且具有时间序列建模专业知识的分析师相对稀缺时。为了解决这些挑战,我们描述了一种实用的、可扩展的预测方法,将可配置的模型与分析师参与的性能分析相结合。我们提出了一个模块化回归模型,具有可解释的参数,可以由对时间序列具有领域知识的分析师直观地调整。我们描述了性能分析来比较和评估预测过程,并自动标记需要人工审查和调整的预测。帮助分析师最有效地利用其专业知识的工具能够可靠地、实践地预测业务时间序列。
1、介绍
预测是数据科学中的一项核心任务,对组织内的许多活动都至关重要。例如,各行业的组织必须进行容量规划,以有效地分配有限资源,并进行目标设定,以衡量相对基准的绩效。然而,对于机器和大多数分析师来说,生成高质量的预测并不容易。我们观察到在创建业务预测的实践中存在两个主要问题。首先,完全自动化的预测技术往往难以调整,并且往往过于僵化,无法纳入有用的假设或启发式方法。其次,负责组织内数据科学任务的分析师通常对所支持的特定产品或服务具有深入的领域专业知识,但往往没有时间序列预测的培训。因此,能够产生高质量预测的分析师非常罕见,因为预测是一项需要丰富经验的专业技能。
结果是,对高质量预测的需求往往远远超过了它们的生产速度。这一观察结果是我们进行研究的动机,我们打算为在不同规模下产生预测提供一些有用的指导。
我们首先考虑的两种规模是:1)适用于大量进行预测的人员,可能没有时间序列方法的培训;2)适用于各种可能具有特殊特征的预测问题。在第3节中,我们提出了一个时间序列模型,它足够灵活,适用于各种业务时间序列,同时可以由非专家配置,这些非专家可能对数据生成过程具有领域知识,但对时间序列模型和方法了解有限。
我们所讨论的第三种规模是在大多数实际情况下,将会创建大量的预测,因此需要高效自动的方式来评估和比较它们,并在性能较差时及时发现。当进行数百甚至数千个预测时,让机器来进行模型评估和比较的工作变得非常重要,同时还要有效地利用人类反馈来解决性能问题。在第4节中,我们描述了一个预测评估系统,该系统利用模拟的历史预测来估计样本外性能,并识别存在问题的预测,供人类分析人员了解出了什么问题并进行必要的模型调整。
值得注意的是,我们并不关注典型的规模考虑因素:计算和存储。我们发现,在大量时间序列的预测中,计算和基础设施问题相对来说比较简单,通常这些拟合过程很容易进行并行处理,并且预测结果也不难存储在关系数据库中。我们在实践中观察到的实际规模问题涉及到预测问题的多样性引入的复杂性,以及在生成了大量预测之后如何建立对其的信任。
我们在图1中总结了我们在大规模业务预测中的“分析师在回路中”的方法。我们首先使用灵活的规范对时间序列进行建模,每个参数都有直观的人类解释。然后,我们为该模型和一组合理的基准线在各种历史模拟预测日期上生成预测,并评估预测性能。当预测性能较差或其他方面需要人工干预时,我们按优先顺序将这些潜在问题通知给人类分析师。分析师可以检查预测结果,并根据这些反馈可能调整模型。
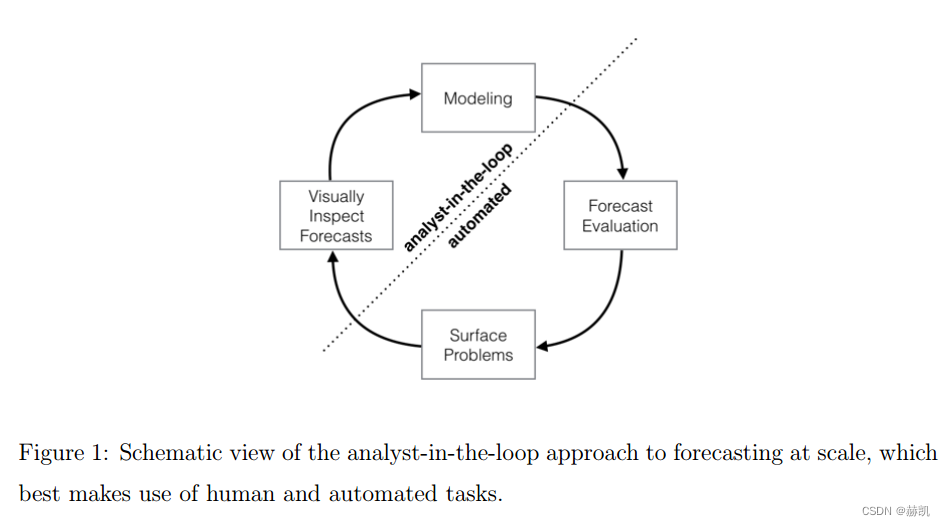
2、时间业务序列的特点
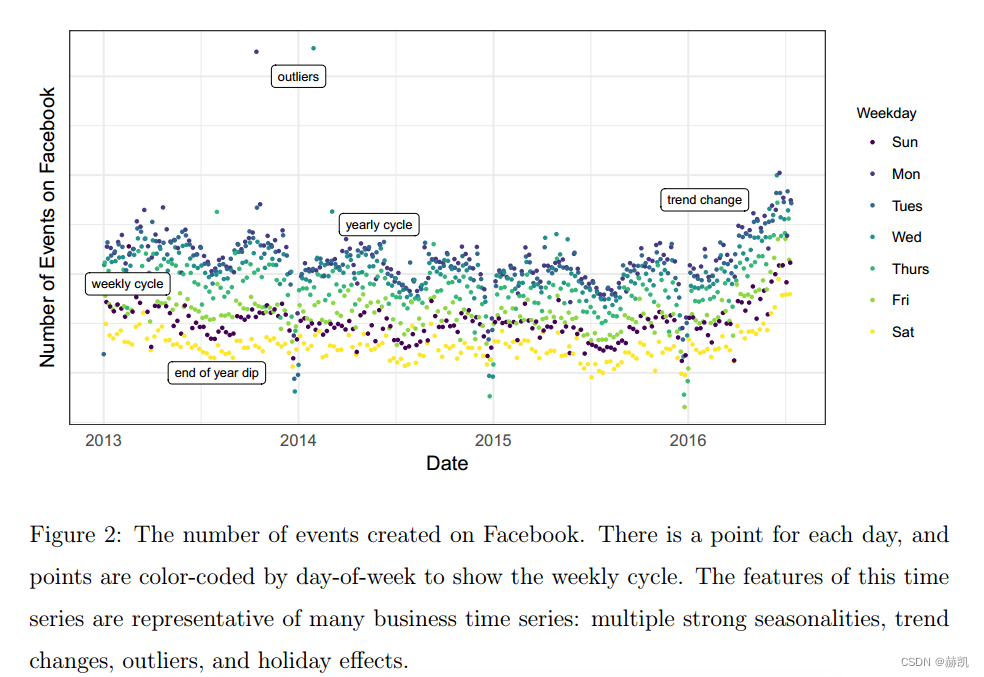
商业预测问题的有多样性和共同性。以Facebook活动的时间序列数据为例进行说明,数据显示了每天在Facebook上创建的活动数量。这个时间序列表现出明显的季节效应,包括每周和每年的周期性变化,以及圣诞节和新年期间的显著下降。这些季节效应是由人类活动产生的时间序列中自然而然地出现的。此外,该时间序列在最近六个月显示了明显的趋势变化,可能是由于新产品或市场变化的影响。同时,真实的数据通常会存在异常值,这个时间序列也不例外。
这个时间序列说明了完全自动化方法在产生合理预测方面的困难。图3展示了使用R语言中的forecast包中几种自动化方法进行的预测。这些方法分别是:auto.arima,它拟合一系列ARIMA模型并自动选择最佳模型;ets,它拟合一系列指数平滑模型并选择最佳模型;snaive,一种具有每周季节性的随机游走模型;tbats,一种具有每周和每年季节性的TBATS模型。从图中可以看出,这些方法在匹配时间序列的特征方面都存在困难。自动ARIMA方法在趋势发生变化时容易产生大的趋势误差,并且无法捕捉到任何季节性。指数平滑和季节性随机游走方法能够捕捉到每周的季节性,但无法捕捉到更长期的季节性。所有这些方法都对年末的下降过度反应,因为它们没有充分建模年度季节性。
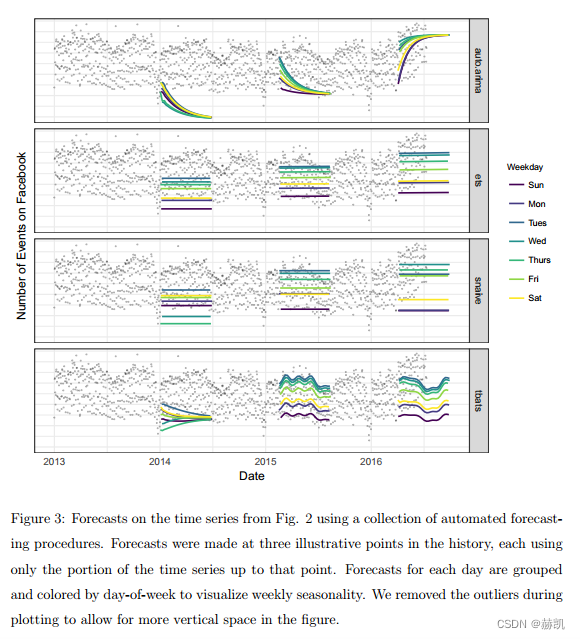
当预测结果不理想时,我们希望能够调整方法的参数以适应具体问题。然而,调整这些方法需要对底层时间序列模型的工作原理有深入的了解。例如,自动ARIMA方法的第一个输入参数是差分、自回归分量和移动平均分量的最大阶数。普通分析师通常不知道如何调整这些阶数以避免图3中的行为,这是一种难以扩展的专业知识。
3、Prophet预测模型
现在我们描述一个时间序列预测模型,设计用于处理图2中所见到的业务时间序列的共同特征。重要的是,它还被设计为具有直观的参数,可以进行调整,而无需知道底层模型的详细信息。这对于分析师有效地调整模型是必要的,如图1所述。我们的实现以Python和R的形式提供作为开源软件,称为Prophet(https://facebook.github.io/prophet/)。
我们使用分解时间序列模型(Harvey&Peters 1990),其中包括三个主要模型组件:趋势、季节性和节假日。它们组合在以下方程中:
y
(
t
)
=
g
(
t
)
+
s
(
t
)
+
h
(
t
)
+
ε
t
y(t)=g(t)+s(t)+h(t)+ε_t
y(t)=g(t)+s(t)+h(t)+εt (1)
这里,g(t)是趋势函数,用于建模时间序列值的非周期性变化,s(t)表示周期性变化(例如,每周和每年的季节性),h(t)表示在一个或多个日期上可能不规则安排的假日效应。误差项 ε t ε_t εt表示模型无法适应的任何特异性变化;稍后,我们将对εt做出参数假设,即服从正态分布。
这个规范类似于广义加性模型(GAM)(Hastie&Tibshirani 1987),一类回归模型,其中对回归器应用了潜在非线性平滑器。在这里,我们只使用时间作为回归器,但可能使用时间的几个线性和非线性函数作为组件。将季节性建模为加法组件的方法与指数平滑(Gardner 1985)采用相同的方法。通过对数转换,可以实现乘法季节性,其中季节效应是乘以g(t)的因子。
GAM的优点在于它很容易进行分解,并根据需要适应新的组件,例如当发现新的季节性来源时。GAM也非常快速适配,可以使用反向逐步回归或L-BFGS(Byrd等,1995)(我们更喜欢后者),以便用户可以交互地更改模型参数。
实际上,我们将预测问题视为一种曲线拟合的过程,这与明确考虑数据中时间依赖结构的时间序列模型本质上是不同的。虽然我们放弃了使用生成模型(如ARIMA)的一些重要推断优势,但这种规范提供了许多实际优势:
- 灵活性:我们可以轻松地适应具有多个周期的季节性,并让分析人员对趋势做出不同的假设。
- 与ARIMA模型不同,测量值不需要定期间隔,我们也不需要插值缺失值,例如从去除异常值中插值。
- 拟合速度非常快,允许分析人员交互式地探索许多模型规范,例如在Shiny应用程序中(Chang等,2015)。
- 预测模型具有易于解释的参数,分析人员可以更改这些参数以对预测施加假设。此外,分析人员通常具有回归的经验,并且很容易将模型扩展到包括新组件。
自动预测有着悠久的历史,有许多方法专门针对特定类型的时间序列(Tashman&Leach 1991,De Gooijer&Hyndman 2006)。我们的方法受到Facebook预测的时间序列的特性(分段趋势、多重季节性、浮动假日)以及大规模预测所涉及的挑战的驱动。
3.1、趋势模型
我们已经实现了两种趋势模型,涵盖了许多Facebook应用程序:饱和增长模型和分段线性模型。
3.1.1、非线性饱和增长
对于增长预测,数据生成过程的核心组成部分是对人口增长的模型以及预期的持续增长模式的建模。在Facebook上进行增长建模通常类似于自然生态系统中的人口增长(例如Hutchinson 1978),其中存在非线性增长,在达到一个承载能力后趋于饱和。例如,在某个特定区域内,Facebook用户数量的承载能力可能是可以接入互联网的人数。这种增长通常使用逻辑增长模型进行建模,在其最基本的形式下是:
g ( t ) = C 1 + e x p ( − k ( t − m ) ) g(t)=\frac{C}{1+exp(-k(t-m))} g(t)=1+exp(−k(t−m))C (2)
其中C为承载能力,k为增长率,m为偏移参数。t是时间,随着时间的增长,分母从小于1边长大于1,导致g(t)开始会很快增大,到后来变缓,直到无限接近C。
在 Facebook 的增长中有两个重要方面没有被上面公式所捕捉到。首先,承载能力并非恒定的,随着世界范围内能够接入互联网的人数增加,增长上限也会相应增加。因此,我们用一个随时间变化的承载能力 C(t) 替代了固定的容量 C。其次,增长率也并非恒定的。新产品可以深刻地改变某个地区的增长速率,因此模型必须能够融合不同的速率以适应历史数据。
我们通过明确定义增长率允许改变的变更点来将趋势变化纳入增长模型。假设在时刻
s
j
s_j
sj 处存在 S 个变更点,即 j = 1…S。我们定义一个速率调整的向量
δ
∈
R
S
δ\in \mathbb{R}^S
δ∈RS,其中
δ
j
δ_j
δj 表示在时刻
s
j
s_j
sj 出现的速率变化。任意时刻 t 的速率则是基本速率 k,再加上该时刻之前的所有调整值之和
k
+
∑
j
:
t
>
s
j
δ
j
k+\sum_{j:t>s_j}^{}δ_j
k+∑j:t>sjδj。这通过定义向量
a
(
t
)
∈
0
,
1
S
a(t)\in{0, 1}^S
a(t)∈0,1S来更清晰地表示,就像下面这样:
a
j
(
t
)
=
{
1
,
i
f
t
⩾
s
j
,
0
,
o
t
h
e
r
w
i
s
e
.
a_j(t)= \left\{\begin{matrix} 1,&if\space t\geqslant s_j, \\ 0,& otherwise. \end{matrix}\right.
aj(t)={1,0,if t⩾sj,otherwise.
则在时间t的速率为 k + a ( t ) T δ k+a(t)^\texttt{T}δ k+a(t)Tδ。当调整速率k时,还必须调整偏移参数m以连接分段的端点。在变化点j处的正确调整可以很容易地计算为
γ j = ( s j − m − ∑ l < j γ l ) ( 1 − k + ∑ l < j δ l k + ∑ l ⩽ j δ l ) γ_j=(s_j-m-\sum_{l<j}^{}γ_l)(1-\frac{k+\sum_{l<j}^{}δ_l}{k+\sum_{l\leqslant j}^{}δ_l}) γj=(sj−m−∑l<jγl)(1−k+∑l⩽jδlk+∑l<jδl)
分段逻辑增长模型
g ( t ) = C ( t ) 1 − e x p ( − k + a ( t ) T δ ) ( t − ( m + a ( t ) T γ ) ) g(t)=\frac{C(t)}{1-exp(-k+a(t)^{\texttt{T}}δ)(t-(m+a(t)^{\texttt{T}}γ))} g(t)=1−exp(−k+a(t)Tδ)(t−(m+a(t)Tγ))C(t) (3)
我们模型中的一个重要参数集是 C(t),即系统在任意时间点的预期容量。分析人员通常能够洞察市场规模并据此设置这些参数。此外,还可能存在外部数据来源可以提供承载能力,比如世界银行的人口预测数据。
在这里提出的 Logistic 增长模型是广义 Logistic 增长曲线的一个特例,而广义 Logistic 增长曲线只是 Sigmoid 曲线的一种类型。将这一趋势模型扩展到其他曲线族是直截了当的。
3.1.2、具有变化点的线性趋势
对于没有表现出饱和增长的预测问题,分段恒定增长率提供了一个简洁且通常有用的模型。这里的趋势模型是:
g ( t ) = ( k + a ( t ) T δ ) t + ( m + a ( t ) T γ ) g(t)=(k+a(t)^{\texttt{T}}δ)t+(m+a(t)^{\texttt{T}}γ) g(t)=(k+a(t)Tδ)t+(m+a(t)Tγ) (4)
其中,与之前一样,k是生长速率,δ有速率调整,m是偏移参数, γ j γ_j γj设置为 − s j δ j −s_jδ_j −sjδj,以使函数连续。
3.1.3、自动转换点选择
变更点
s
j
s_j
sj 可以由分析人员使用已知的产品发布日期和其他改变增长的事件来确定,或者可以根据一组候选项自动选择。使用公式(3)和(4)中的表达式,可以自然地对 δ 设置稀疏先验分布来进行自动选择。
我们通常会指定大量的变更点(例如,对于几年的历史数据,每个月一个变更点),并使用先验分布
δ
j
∼
L
a
p
l
a
c
e
(
0
;
τ
)
δ_j ∼ Laplace(0; τ)
δj∼Laplace(0;τ)。参数
τ
τ
τ 直接控制模型在调整速率方面的灵活性。重要的是,对调整项
δ
δ
δ 使用稀疏先验不会对主要的增长率 k 产生影响,因此当
τ
τ
τ 趋近于0时,拟合结果将归约为标准的(非分段)Logistic或线性增长模型。
3.1.4、趋势预测的不确定性
当模型被推广至历史数据以外进行预测时,趋势将具有恒定的速率。我们通过向前延伸生成模型来估计预测趋势的不确定性。趋势的生成模型是,在历史的 T 个点上存在 S 个变更点,每个变更点都有一个速率变化 δ j ∼ L a p l a c e ( 0 ; τ ) δ_j ∼ Laplace(0; τ) δj∼Laplace(0;τ)。我们通过用从数据中推断出的方差取代 τ τ τ 来模拟未来速率变化,使其模拟过去的情况。在完全的贝叶斯框架中,这可以通过对 τ τ τ 设置分层先验来获得其后验概率,否则我们可以使用速率尺度参数的最大似然估计值 λ = 1 S ∑ j = 1 S ∣ δ j ∣ λ = \frac{1}{S} \sum_{j=1}^{S} |δ_j| λ=S1∑j=1S∣δj∣。未来的变更点是以随机方式抽样的,以使变更点的平均频率与历史中的频率相匹配:
∀ j > T , { δ j = 0 w . p . T − S T , δ j ∼ L a p l a c e ( 0 ; τ ) w . p . S T . \forall_j>T, \left\{\begin{matrix} δ_j =0 \space \mathrm{w}.\mathrm{p}. \space \frac{T-S}{T}, \\ δ_j ∼ Laplace(0; τ) \space \mathrm{w}.\mathrm{p}. \space \frac{S}{T}. \end{matrix}\right. ∀j>T,{δj=0 w.p. TT−S,δj∼Laplace(0;τ) w.p. TS.
因此,我们通过假设未来的频率和速率变化的平均值与历史上观察到的相同,来衡量预测趋势的不确定性。一旦从数据中推断出 λ λ λ,我们使用这个生成模型来模拟可能的未来趋势,并利用模拟的趋势来计算不确定性区间。
假设趋势在未来以与历史上相同的频率和幅度变化,是相当强的假设,因此我们不指望不确定性区间能够完全覆盖。然而,它们仍然是对不确定性水平的有用指示,尤其是对过度拟合的指示。随着 τ τ τ 的增加,模型在拟合历史时具有更大的灵活性,因此训练误差会降低。然而,当向前进行预测时,这种灵活性将产生宽广的不确定性区间。