苏米特·班迪帕迪亚
一、说明
特征工程是利用领域知识从原始数据中提取特征的过程。这些功能可用于提高机器学习算法的性能。本篇叙述在特征选择过程的若干数据处理。
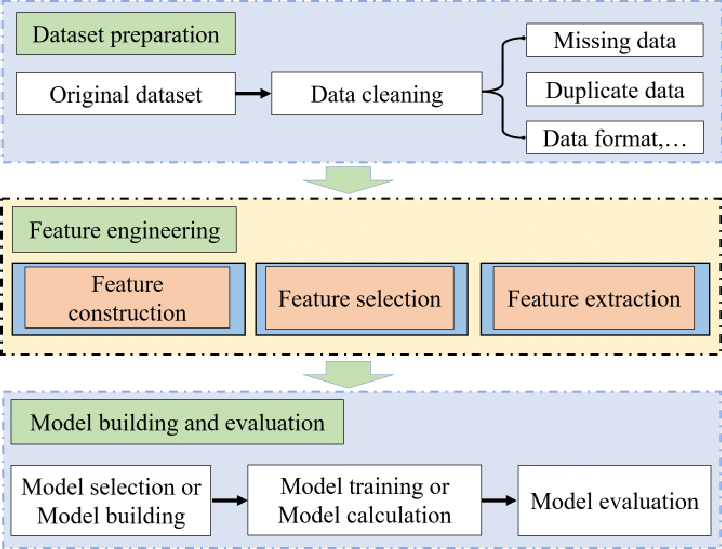
一般来说,特征工程有以下子步骤:
- 特征转换
- 特征构建
- 特征选择
- 特征提取
二、特征转换的缺失数据处理
在特征变换中,我们做了以下几种处理
2.1 缺失值插补
在现实世界中,通常不可能找到完整且没有缺失值或NaN值的数据。因此,我们可以删除包含这些缺失值的行,或者执行插补(填充缺失值)以确保 ML 模型处理这些数据。
要从 pandas 数据框中删除行,我们使用以下命令
#Assuming data is store in df dataframe
df.isnull().sum()
#This returns the count of all the missing values in the columns
#In order to remove the missing values, we use drop function
df.drop(inplace=True)2.2 数据插补
它是用各种插补策略(例如均值、中位数和众数插补)替换缺失值的过程。然而,也可以通过根据领域知识为数据分配值来随机进行插补。
def mean_imputation(data, inplace=False):
"""
This function replaces the missing values in the data with the average (mean) value of the data.
Parameters:
- data: The input data with missing values.
- inplace: A boolean indicating whether to modify the data in place or return a new copy.
If True, the missing values are filled in the original data; if False, a new copy with filled values is returned.
(Default: False)
"""
data.fillna(data.mean(), inplace=inplace)
def median_imputation(data, inplace=False):
"""
This function replaces the missing values in the data with the median value of the data.
Parameters:
- data: The input data with missing values.
- inplace: A boolean indicating whether to modify the data in place or return a new copy.
If True, the missing values are filled in the original data; if False, a new copy with filled values is returned.
(Default: False)
"""
data.fillna(data.median(), inplace=inplace)
def mode_imputation(data, inplace=False):
"""
This function replaces the missing values in the data with the mode value of the data.
Parameters:
- data: The input data with missing values.
- inplace: A boolean indicating whether to modify the data in place or return a new copy.
If True, the missing values are filled in the original data; if False, a new copy with filled values is returned.
(Default: False)
"""
data.fillna(data.mode(), inplace=inplace)替代方法
threshold = 0.7
#Dropping columns with missing value rate higher than threshold
data = data[data.columns[data.isnull().mean() < threshold]]
#Dropping rows with missing value rate higher than threshold
data = data.loc[data.isnull().mean(axis=1) < threshold]我们还可以使用预测插补或使用机器学习模型的插补
在这种方法中,不是使用均值、中位数或众数等汇总统计来填充缺失值,而是使用机器学习模型根据在没有缺失值的剩余特征中观察到的模式来预测缺失值。
三、处理分类特征
One-hot 编码是一种用于将分类变量表示为二进制向量的技术。它通常用于机器学习和数据预处理任务。one-hot 编码过程将每个分类值转换为一个新的二进制特征,其中值的存在或不存在分别由 1 或 0 表示。
此方法将难以理解算法的分类数据更改为数字格式,并使您能够对分类数据进行分组而不会丢失任何信息。
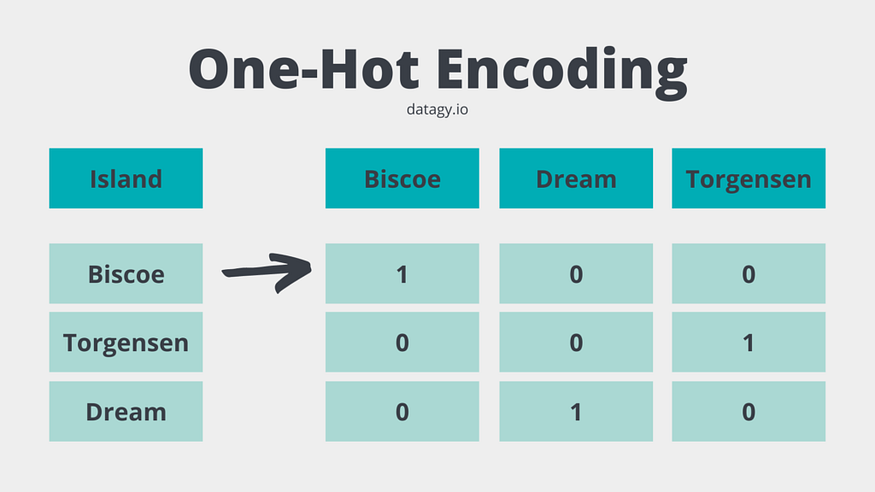
一种热门编码技术
在 one-hot 编码中,分类列中的每个不同值都由单独的二进制列表示。这意味着对于列中的 N 个不同值,将创建 N 个二进制列,每列代表特定值的存在或不存在。这种方法确保每个类别都有自己独立的二进制特征,使机器学习算法更容易理解和处理分类数据。
encoded_columns = pd.get_dummies(data['column'])
data = data.join(encoded_columns).drop('column', axis=1)四、异常值检测
异常值检测是识别数据集中明显偏离大多数数据点的观测值的过程。
检测异常值在数据分析和机器学习中非常重要,因为它们会对模型的结果和性能产生重大影响。
统计方法:
- Z 分数:计算每个数据点的 Z 分数,并标记 Z 分数高于特定阈值的数据点。
import numpy as np
def zscore_outlier_detection(data, threshold=3):
z_scores = (data - np.mean(data)) / np.std(data)
outliers = np.abs(z_scores) > threshold
return outliers- 改进的 Z 得分方法:与 Z 得分方法类似,但使用稳健的变异估计,例如中值绝对偏差。
from scipy.stats import median_absolute_deviation
def modified_zscore_outlier_detection(data, threshold=3.5):
median = np.median(data)
median_abs_dev = median_absolute_deviation(data)
modified_z_scores = 0.6745 * (data - median) / median_abs_dev
outliers = np.abs(modified_z_scores) > threshold
return outliers- Tukey 栅栏:将异常值识别为低于下栅栏 (Q1 — k * IQR) 或高于上栅栏 (Q3 + k * IQR) 的值,其中 Q1 和 Q3 是第一和第三四分位数,IQR 是四分位距。
def tukey_fences_outlier_detection(data, k=1.5):
q1 = np.percentile(data, 25)
q3 = np.percentile(data, 75)
iqr = q3 - q1
lower_fence = q1 - k * iqr
upper_fence = q3 + k * iqr
outliers = (data < lower_fence) | (data > upper_fence)
return outliers- K 最近邻 (KNN):测量每个点与其 k 个最近邻的距离,并将距离较大的点识别为异常值。
from sklearn.neighbors import NearestNeighbors
def knn_outlier_detection(data, k=5, threshold=1.5):
neigh = NearestNeighbors(n_neighbors=k)
neigh.fit(data)
distances, _ = neigh.kneighbors(data)
median_distance = np.median(distances[:, -1])
normalized_distances = distances[:, -1] / median_distance
outliers = normalized_distances > threshold
return outliers- 局部异常值因子:计算每个点与其相邻点相比的局部密度,并将密度明显较低的点标记为异常值。
from sklearn.neighbors import LocalOutlierFactor
def lof_outlier_detection(data, contamination=0.1):
lof = LocalOutlierFactor(n_neighbors=20, contamination=contamination)
outliers = lof.fit_predict(data) == -1
return outliers处理异常值的另一个选择是限制它们而不是丢弃它们。
#Capping the outlier rows with percentiles
upper_lim = data['column'].quantile(.95)
lower_lim = data['column'].quantile(.05)
data.loc[(df[column] > upper_lim),column] = upper_lim
data.loc[(df[column] < lower_lim),column] = lower_lim五、特征缩放
特征缩放是机器学习中的预处理步骤,涉及将数据集的数值特征转换为通用尺度。这很重要,因为当特征规模相似时,许多机器学习算法表现更好或收敛得更快。
特征缩放的几种方法:
5.1 标准化(Z 分数归一化)
此方法将特征缩放至零均值和单位方差。它减去特征的平均值并除以标准差。标准化的公式为: x_scaled = (x — Mean(x)) / std(x)
标准化可确保每个特征的平均值为 0且标准差为 1,从而使所有特征具有相同的量级。

x = 观察值,μ = 平均值,σ = 标准差
from sklearn.preprocessing import StandardScaler
# Create an instance of StandardScaler
scaler = StandardScaler()
# Assuming your data is stored in a 2D array or dataframe X
# Fit the scaler to your data
scaler.fit(X)
# Transform the data
X_scaled = scaler.transform(X)
# The transformed data is now normalized using Z-score normalization5.2 最小-最大缩放
此方法将特征缩放到指定范围(通常在 0 到 1 之间)。它减去特征的最小值并除以范围(最大值减去最小值)。最小-最大缩放的公式为: x_scaled = (x — min(x)) / (max(x) — min(x))
![]()
from sklearn.preprocessing import MinMaxScaler
import numpy as np
# 4 samples/observations and 2 variables/features
data = np.array([[4, 6], [11, 34], [10, 17], [1, 5]])
# create scaler method
scaler = MinMaxScaler(feature_range=(0,1))
# fit and transform the data
scaled_data = scaler.fit_transform(data)
print(scaled_data)
# [[0.3 0.03448276]
# [1. 1. ]
# [0.9 0.4137931 ]
# [0. 0. ]]5.3 最大绝对缩放
此方法将特征缩放到范围 [-1, 1]。它将每个特征值除以该特征中的最大绝对值。max-abs 缩放的公式为: x_scaled = x / max(abs(x))

from sklearn.preprocessing import MaxAbsScaler
# Create an instance of MaxAbsScaler
scaler = MaxAbsScaler()
# Assuming your data is stored in a 2D array or dataframe X
# Fit the scaler to your data
scaler.fit(X)
# Transform the data
X_scaled = scaler.transform(X)
# The transformed data is now scaled using max-abs scaling特征缩放方法的选择取决于数据集的特征和所使用的机器学习算法的要求。