💻文章目录
- AVL树
- 概念
- AVL的查找
- AVL树的插入
- 代码部分
- AVL树的定义
- 查找
- 插入
- 旋转
- 📓总结
AVL树
概念
AVL树又名高度平衡的二叉搜索树,由G. M. Adelson-Velsky和E. M. Landis发明,顾名思义,其任意节点的左右子树最大高度差都不超过1,以此来阻止二叉搜索树退化成为单叉树这种情况。
AVL树具有以下的特性:
- 任意节点的左右子树最大高度差不超过1
- 所有节点的左节点都比父节点小。
- 所有节点的右节点都比父节点大。
- 它的左右子树都是AVL树。
- 中序遍历是有序的
AVL树与普通二叉搜索树的对比:

AVL的查找
AVL树的查找与二叉搜索树基本一致,因为其自身的性质,所以只要查找的数据比当前节点小就要到左节点找,反之就是右节点。
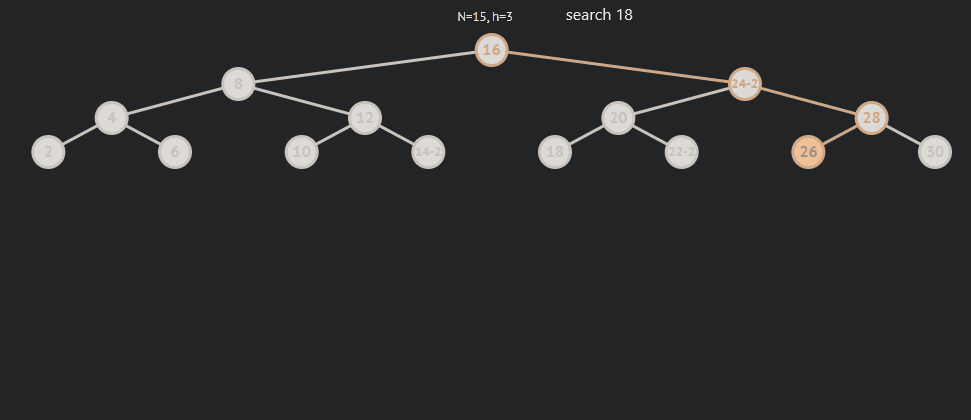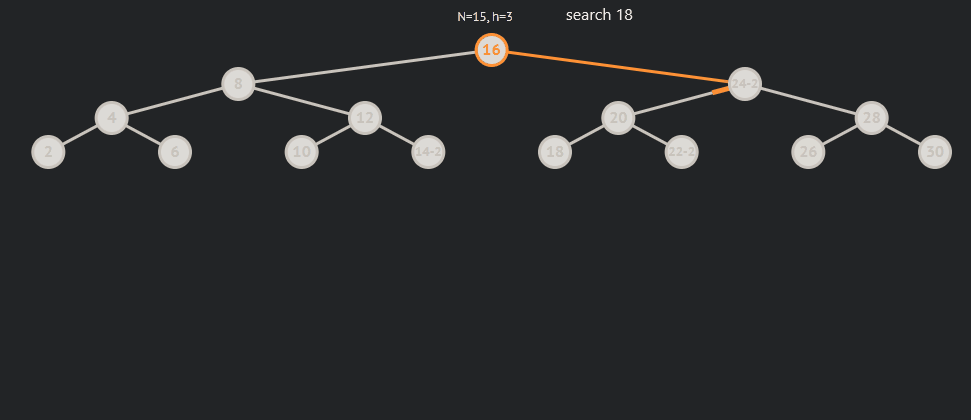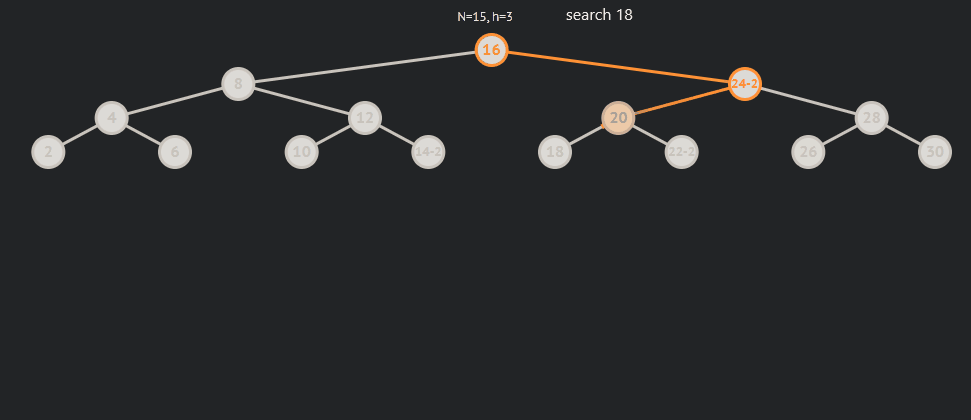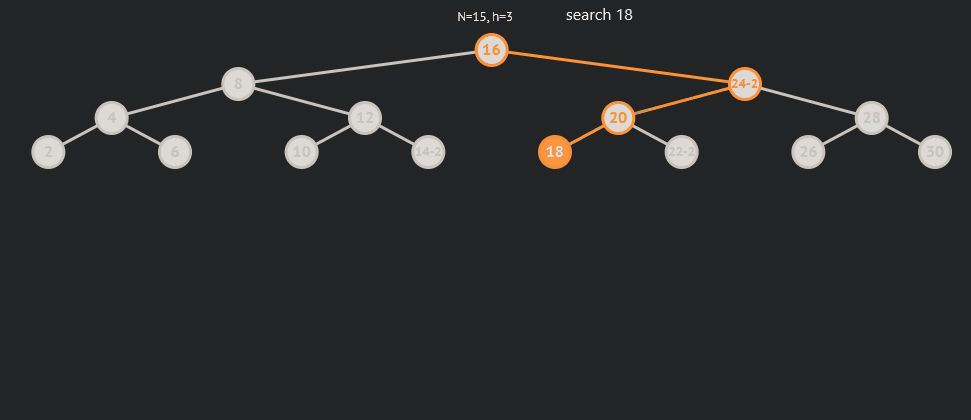
AVL树的插入
在介绍插入前得先说一下平衡因子,这是为了得知插入新结点后树是否还平衡的方式之一。
平衡因子是在每个结点上安置一个数字,如果是新插入的节点则它的数值为0,如果其在双亲节点的右边,则双亲节点的平衡因子++,反之–,然后继续向上调整,直到父节点的因子为0/2/-2。

AVL因为要保持其高度平衡的特性,所以每次插入都要检查其是否平衡,如果不平衡(平衡因子的绝对值大于1),则需要通过旋转来让树保持平衡。
AVL树的旋转大致分为两种情况:
- 极端倾斜(左倾、右倾)
- 非极端倾斜(局部左倾,局部右倾)
极端倾斜:
极端倾斜的情况比较容易解决,如果是右倾,那么只需要让平衡因子为2的节点做左旋运动,然后更新平衡因子即可,左倾则和右倾相反,做右旋操作。
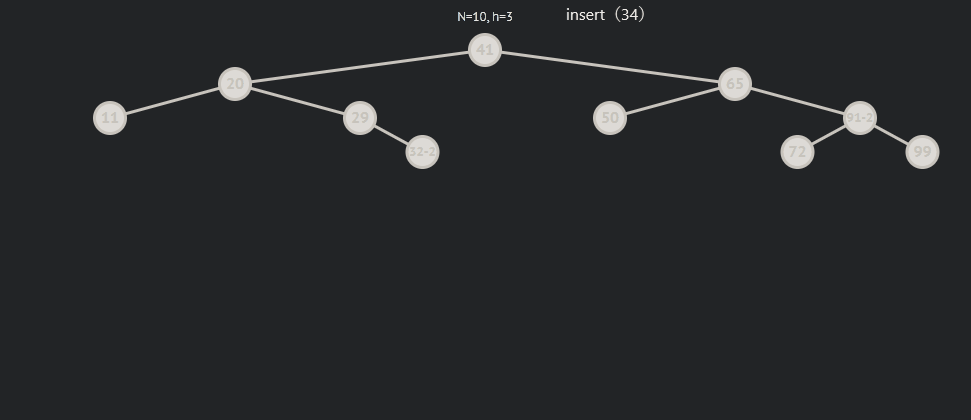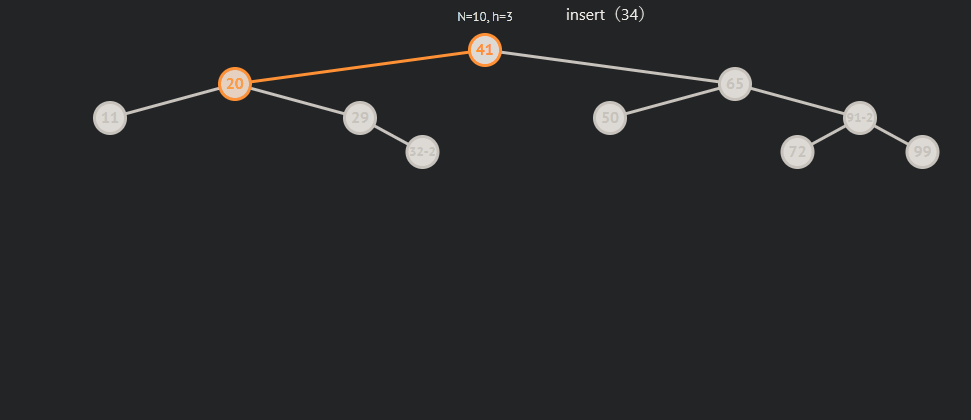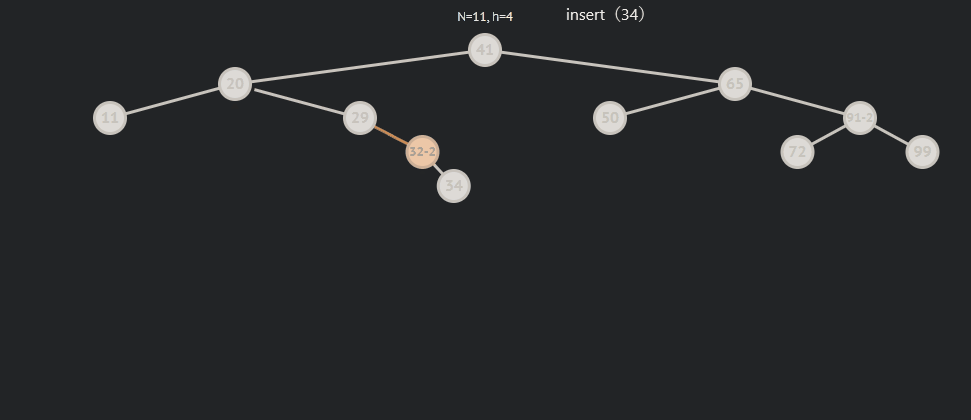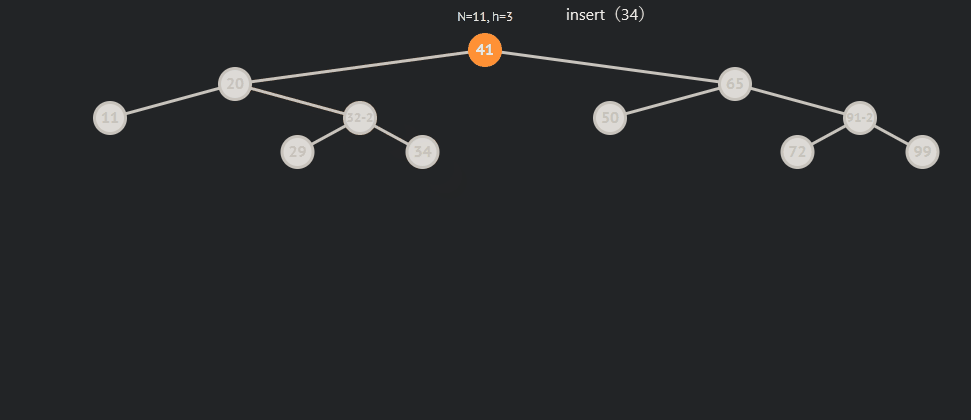
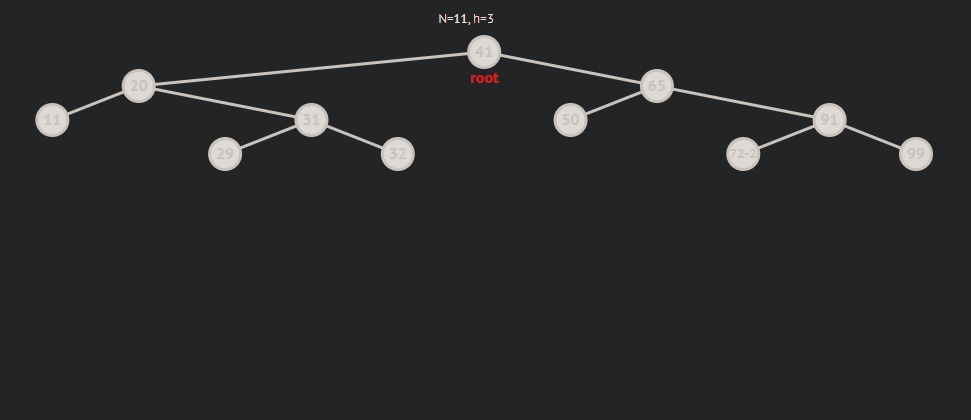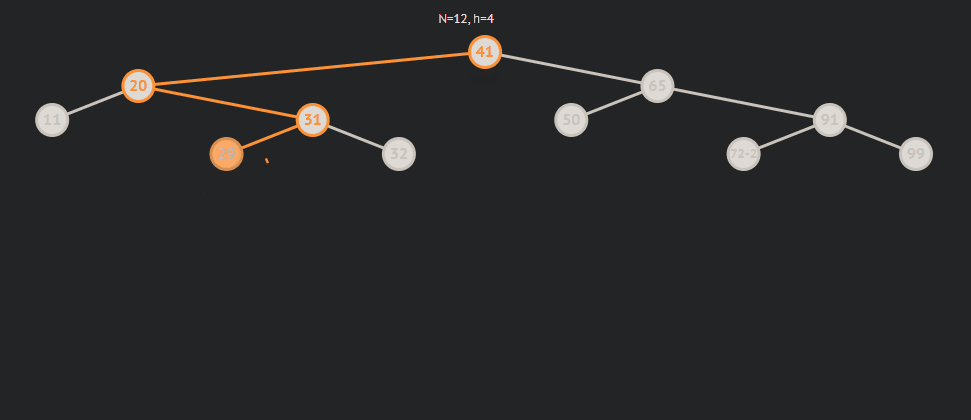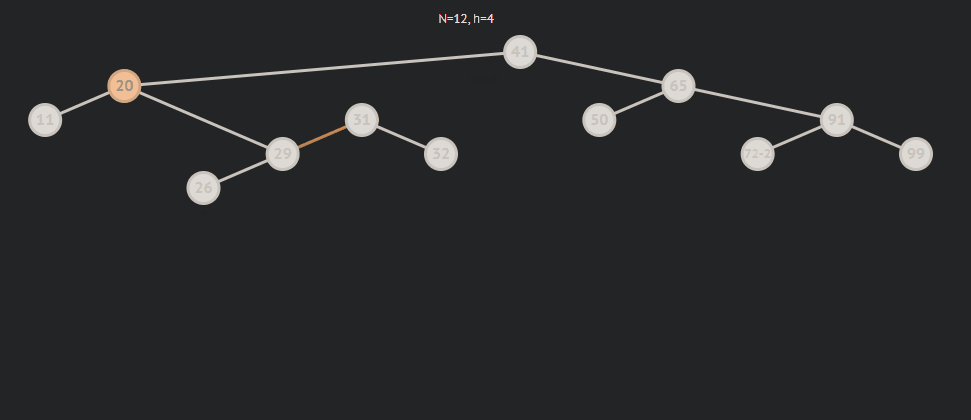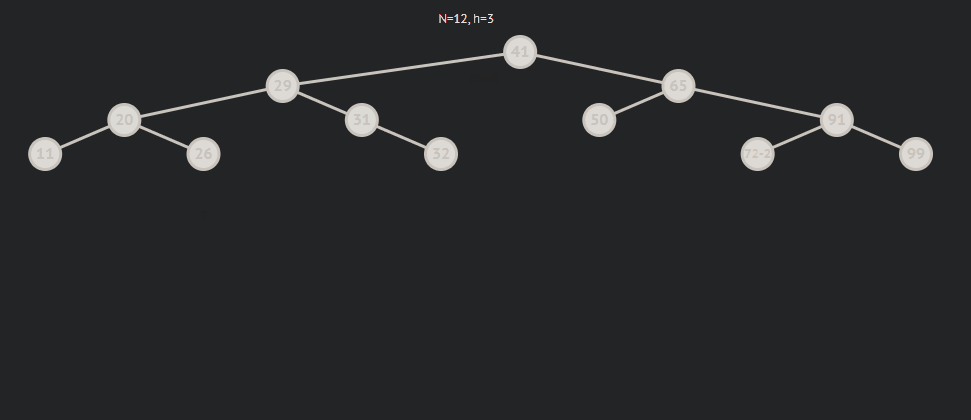
局部倾斜:
局部倾斜分为局部左倾和右倾,而左右倾其中又分为三中情况,为了方便说明,我用parent来表示平衡因子(bf)为2的节点,subR来表示parent->right,subRL来表示subR->left 。
- subRL为0则表示subRL为新增节点
- subRL为1则表示新节点在subRL的右子树
- subRL为-1则表示新节点在subRL的左子树
subRL为0的情况:
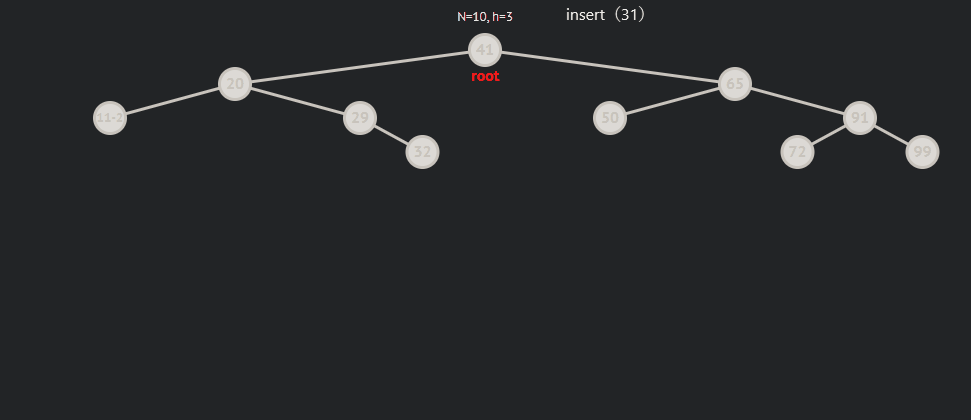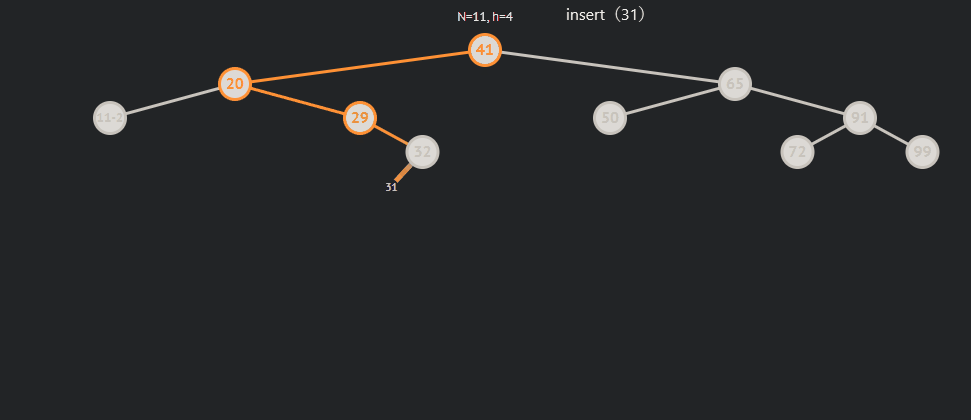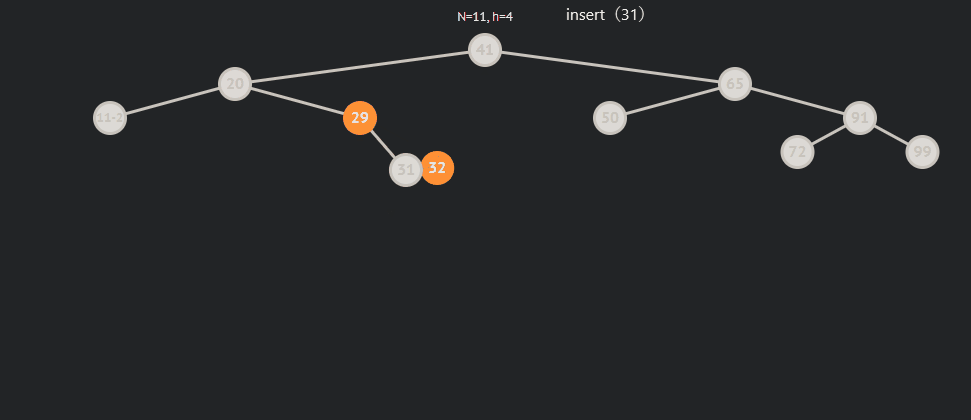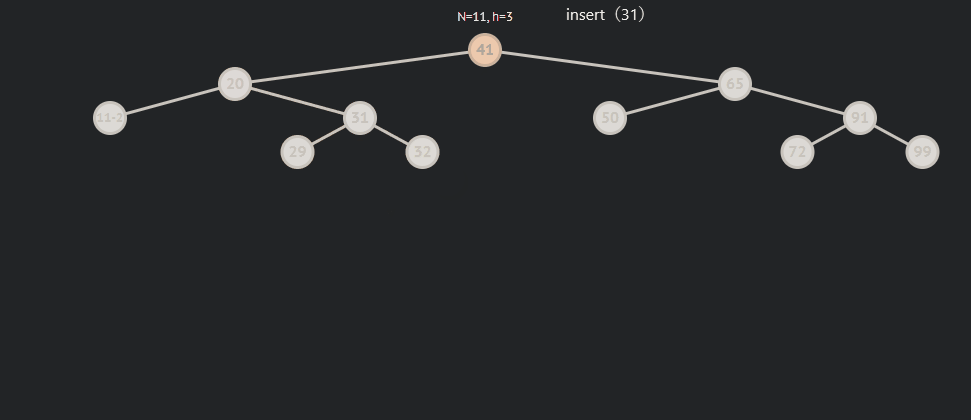
subRL为1的情况:
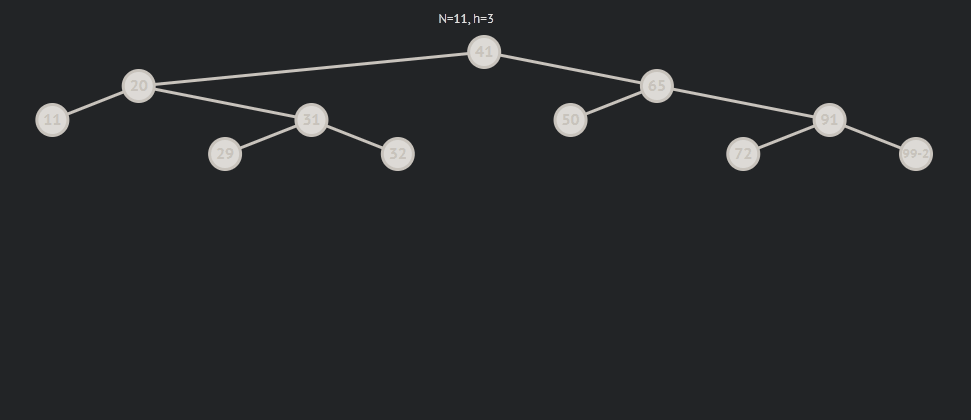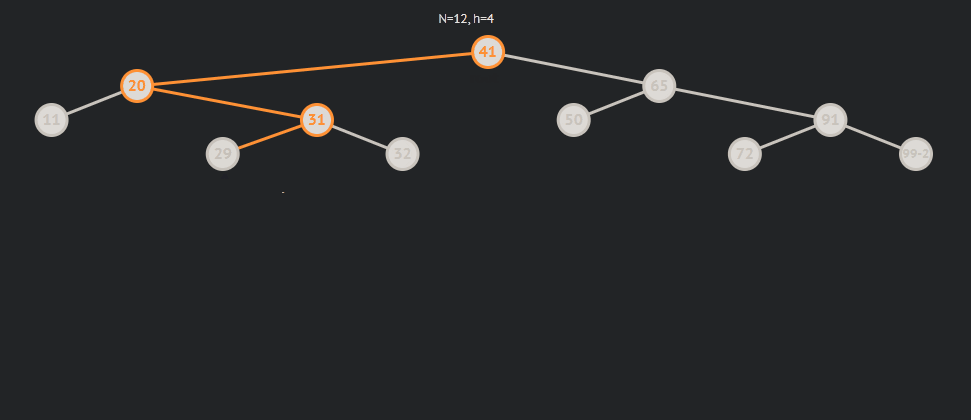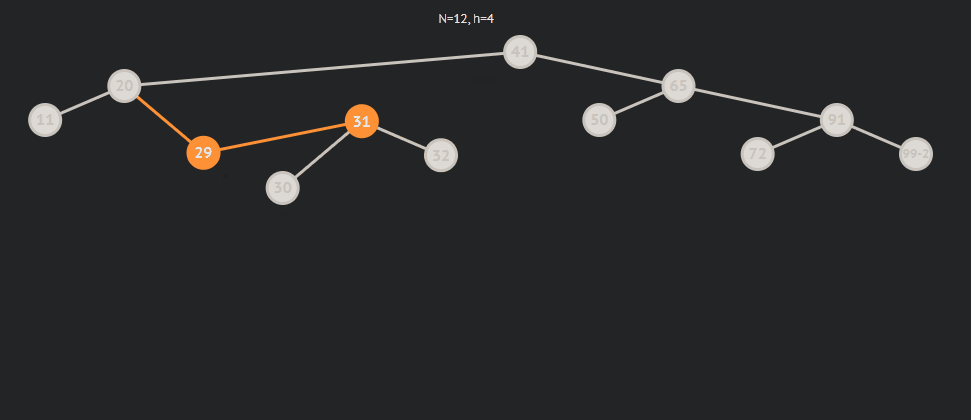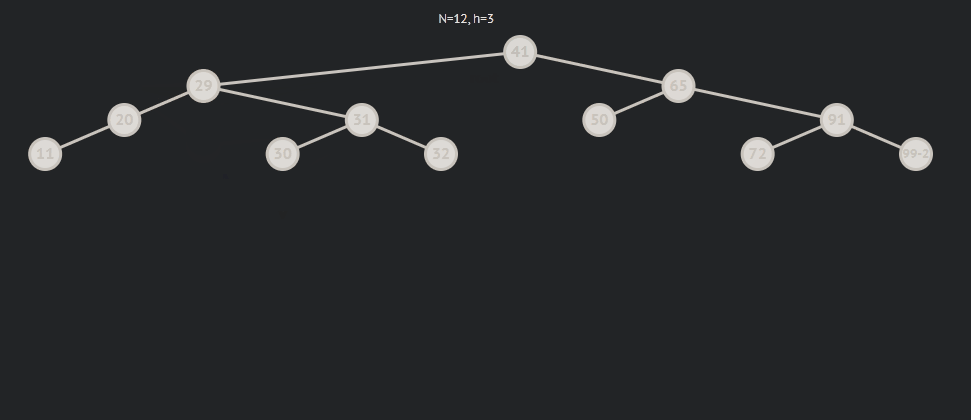
subRL为-1的情况:
代码部分
AVL树的定义
因为我们需要频繁去调整树的平衡,使用普通的二链结构会比较难以控制节点,所以我使用了三叉链的结构,多增加了一个指向父节点的指针。
template<class K, class V>
struct AVLTreeNode
{
AVLTreeNode(const std::pair<K, V> kv)
: _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _kv(kv)
, _bf(0)
{}
AVLTreeNode<K, V>* _left; //左节点
AVLTreeNode<K, V>* _right; //右节点
AVLTreeNode<K, V>* _parent; //父节点
std::pair<K, V> _kv; //使用pair当作数据
int _bf; // 节点的平衡因子
};
查找
二叉搜索树与AVL树的搜索基本无区别
template <class K, class V>
typename AVLTree<K, V>::Node* AVLTree<K, V>::find(const std::pair<K, V>& data)
{
Node* cur = _root;
while(cur)
{
if(cur->_kv.first < data.first)
{ //到右节点寻找
cur = cur->_right;
}
else if(cur->_kv.first > data.first)
{ //到左节点寻找
cur = cur->_left;
}
else
{ //找到
return cur;
}
}
return cur;
}
插入
AVL树的插入无非也就是弄清楚倾斜的时机和位置,就和上方所说的,AVL树的旋转情况只有极端和非极端的,如果没有出现不平衡则向上调整。
template <class K, class V>
bool AVLTree<K, V>::Insert(const std::pair<K, V> data)
{
if(!_root)
{
_root = new Node(data);
return true;
}
Node* cur = _root;
Node* parent = nullptr;
while(cur) //先搜索
{
if(cur->_kv.first < data.first)
{
parent = cur;
cur = cur->_right;
}
else if(cur->_kv.first > data.first)
{
parent = cur;
cur = cur->_left;
}
else
return false;
}
cur = new Node(data); //创建新节点
cur->_parent = parent; //链接
if(!parent->_left)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
while(parent)
{
if(cur == parent->_left)
parent->_bf--; //这里与上方动图有些许不同,动图与我平衡因子的加减是相反的
else // cur == parent->_right
parent->_bf++;
if(parent->_bf == 0) //为0说明左右节点最大高度差一致
break;
else if(parent->_bf == 1 || parent->_bf == -1) //为1则继续向上调整
{
cur = parent;
parent = parent->_parent;
}
else if(parent->_bf == 2 || parent->_bf == -2) //出现了不平衡的清空
{
if(parent->_bf == 2 && cur->_bf == 1) //极端右倾
{
RotateL(parent); //左倾
}
else if(parent->_bf == -2 && cur->_bf == -1) //极端左倾
{
RotateR(parent); //右倾
}
else if(parent->_bf == 2 && cur->_bf == -1) //局部左倾
{
RotateRL(parent); //先右倾,再左倾
}
else if(parent->_bf == -2 && cur->_bf == 1) //局部右倾
{
RotateLR(parent); //左倾再右倾
}
break;
}
else
assert(false);
}
return true;
}
旋转
AVL树的旋转其难点在于正确的连接节点,与调整平衡因子的数值。
void AVLTree<K, V>::RotateL(Node* parent)
{ //左旋
Node* subR = parent->_right;
Node* subRL = subR->_left;
Node* parentParent = parent->_parent;
parent->_right = subRL; //交换父节点和其右孩子的位置
parent->_parent = subR;
subR->_left = parent;
subR->_parent = parentParent;
if(subRL) //subRL有为空的可能性
subRL->_parent = parent;
if(_root == parent)
{
_root = subR;
}
else
{ //连接祖父节点
if(parent == parentParent->_left)
{
parentParent->_left = subR;
}
else
{
parentParent->_right = subR;
}
}
parent->_bf = subR->_bf = 0; //调整平衡因子
}
void AVLTree<K, V>::RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
Node* parentParent = parent->_parent;
subL->_right = parent;
subL->_parent = parentParent;
parent->_left = subLR;
parent->_parent = subL;
if(subLR)
subLR->_parent = parent;
if(parent == _root)
_root = subL;
else
{
if(parent == parentParent->_left)
parentParent->_left = subL;
else
parentParent->_right = subL;
}
subL->_bf = parent->_bf = 0;
}
void AVLTree<K, V>::RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf; //先记录平衡因子,以防调整后丢失
RotateR(parent->_right);
RotateL(parent);
//调整因子
if(bf == 0) //说明subRL是新增节点
{
parent->_bf = subR->_bf = subRL->_bf = 0;
}
else if(bf == 1) //新增节点在subRL的右子树
{
parent->_bf = -1;
subR->_bf = 0;
subRL->_bf = 0;
}
else if(bf == -1) //新增节点在subRL的右子树
{
subRL->_bf = 0;
subR->_bf = 1;
parent->_bf = 0;
}
else
{
assert(false);
}
}
void AVLTree<K, V>::RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
int bf = subLR->_bf;
RotateL(parent->_left);
RotateR(parent);
if(bf == 0)
{
parent->_bf = subL->_bf = subLR->_bf = 0;
}
else if(bf == -1)
{
parent->_bf = 1;
subL->_bf = 0;
subLR->_bf = 0;
}
else if(bf == 1)
{
subL->_bf = -1;
parent->_bf = 0;
subLR->_bf = 0;
}
else
assert(false);
}
📓总结
AVL的时间复杂度:
| 函数 | 时间复杂度 |
|---|---|
| find | O ( l o g 2 n ) O(log_2n) O(log2n) |
| insert() | O ( l o g 2 n ) O(log_2n) O(log2n) |
📜博客主页:主页
📫我的专栏:C++
📱我的github:github