84.柱状图中最大的矩形

        给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1。求在柱状图中，能够勾勒出来的矩形的最大面积。和 42.接雨水 类似，在由数组组成的柱状图中，根据条件求解。

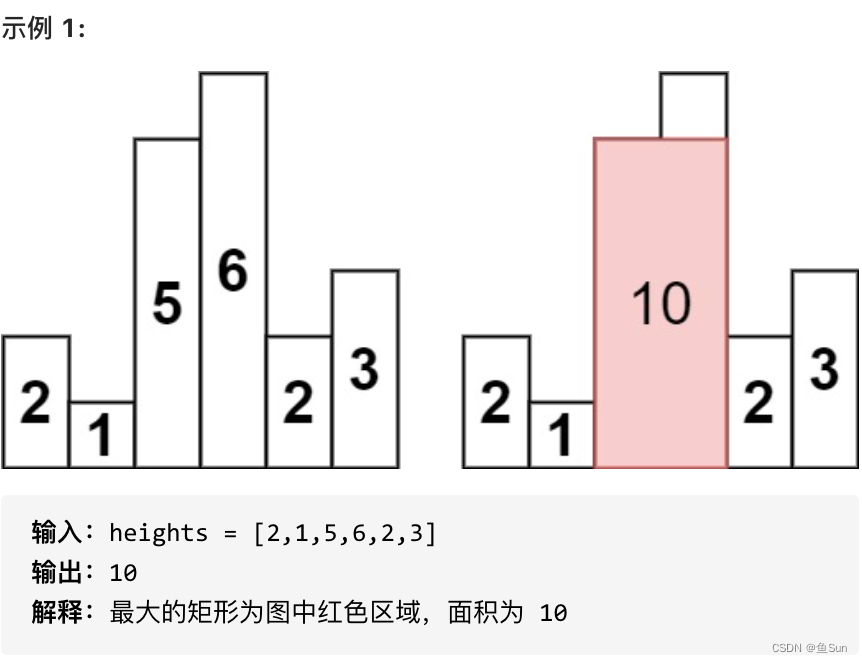
        图来自 代码随想录单调栈章节相关内容，如图所示，图中的柱状图是根据 heights 数组生成的，求解柱状图中形成的矩形的最大面积。与 42.接雨水 问题类似，我们求以每个柱子为基底所形成的矩形的面积，在所有的结果中取最大值。

        例如，求以 4 号柱子为基底形成的矩形的面积，我们需要得到哪些信息？右边第一个更小的柱子高度作为右边界 和 左边第一个更小的柱子高度作为左边界。然后将 高度 × 宽度，得到矩形的面积。4 号柱子对应的矩形面积为：2 * 4 = 8，这里有同学可能会产生疑问，在代码实现中，4 号柱子右边没有高度更小的柱子怎么办？只需要在数组右边填充一个 0 即可，左边同理填充 0。根据上述思路发现，这是一个单调栈问题，在单调栈中以单调递减的顺序存储遍历过得元素。

class Solution {
public:
    int largestRectangleArea(vector<int> &heights) {
        heights.insert(heights.begin(), 0);
        heights.push_back(0);

        stack<int> st;
        int result = 0;

        for (int i = 0; i < heights.size(); ++i) {
            while (!st.empty() && heights[i] < heights[st.top()]) {
                int index = st.top();
                st.pop();

                if (!st.empty()) {
                    int h = heights[index];
                    int w = i - st.top() - 1;
                    result = max(result, h * w);
                }
            }

            st.push(i);
        }

        return result;
    }
};