递归
递归(英语:Recursion),在计算机科学中,递归指的是一个函数在其定义中调用自身的方法。这种技术允许程序解决复杂问题,通过将它们分解为更小、更易管理的相似问题。递归通常与分治策略相关联,后者涉及将一个大问题分解为若干个小问题,单独解决这些小问题,然后将结果合并以得到最终解。
递归函数通常具有以下两个主要特征:
- 基本情况(Base Case):这是递归停止的条件。在达到基本情况时,函数将停止调用自身。例如,在计算阶乘的递归函数中,
0!或1!通常作为基本情况。 - 递归步骤(Recursive Step):在这一步中,函数调用自身来解决子问题。这些子问题是原始问题的更小版本。
在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。
请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
示例1:
输入:A = [2, 1, 0], B = [], C = []
输出:C = [2, 1, 0]
示例2:
输入:A = [1, 0], B = [], C = []
输出:C = [1, 0]
提示:
- A中盘子的数目不大于14个。
思路:
先分析简单情况:
一.n=1 时:直接将这个盘子从A拿出,放到C。
二.n=2 时:假设上面的盘子是甲,下面的盘子是乙。
甲:A->B 乙:A->C 甲:B->C
三.n时 :可以把上面n-1个盘子看出一个整体(一个盘子)甲,下面的第n个盘子是乙。
甲:A->B 乙:A->C 甲:B->C
此时:甲:A->B 这个就是一个小问题,把n-1个盘子从A移动到B,可以用C当媒介—递归
甲:B->C 这个也是一个小问题,把n-1个盘子从B移动到C,可以用A当媒介—递归
#include <iostream>
#include <vector>
using namespace std;
void move(int n, vector<int>& source, vector<int>& target, vector<int>& auxiliary) {
if (n == 1) {
// 直接移动
target.push_back(source.back());
source.pop_back();
} else {
// 移动上面的 n-1 个盘子从 source 到 auxiliary
move(n - 1, source, auxiliary, target);
// 移动底下的盘子从 source 到 target
target.push_back(source.back());
source.pop_back();
// 移动 n-1 个盘子从 auxiliary 到 target
move(n - 1, auxiliary, target, source);
}
}
void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
move(A.size(), A, C, B);
}
int main() {
vector<int> A = {3, 2, 1, 0}; // Tower A
vector<int> B; // Tower B
vector<int> C; // Tower C
hanota(A, B, C);
// Output the result
cout << "Tower C after moving disks: ";
for (int disk : C) {
cout << disk << " ";
}
cout << endl;
return 0;
}
分治算法 (Divide and Conquer)
分治算法是一种特殊类型的递归算法,具体包括以下三个步骤:
- 分解(Divide):将原问题分解成一系列子问题。这些子问题是原问题的较小版本,但与原问题具有相同的形式。
- 解决(Conquer):递归地解决这些子问题。如果子问题足够小,可以直接求解。
- 合并(Combine):将子问题的解合并起来,形成原问题的解。
分治算法的经典例子包括快速排序、归并排序、二分搜索等。在这些算法中,问题被分解成更小的部分,独立解决这些小问题,然后将解合并以解决原始问题。
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104
**进阶:**如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的 分治法 求解。
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
class Solution {
public:
int maxSub(vector<int>& nums, int l, int r){
if(l == r){
return nums[l];
}
// 递归体——分治求解
int mid = (l + r) / 2;
// 左边最大子序和
int lmax = maxSub(nums, l, mid);
// 右边最大子序和
int rmax = maxSub(nums, mid + 1, r);
// 跨越中点的最大子序和
int mmax = mid_sum(nums, l, r, mid);
// 返回三者中的最大值
return max(max(lmax, rmax), mmax);
}
int mid_sum(vector<int>& nums, int l, int r, int mid){
// 从中点向左扩展
int lmax = INT_MIN; // 左边最大值
int sum = 0; // 当前和
for(int i = mid; i >= l; i--){
sum += nums[i];
lmax = max(lmax, sum);
}
// 从中点向右扩展
int rmax = INT_MIN; // 右边最大值
sum = 0; // 当前和
for(int i = mid + 1; i <= r; i++){
sum += nums[i];
rmax = max(rmax, sum);
}
// 返回左右最大值之和
return lmax + rmax;
}
int maxSubArray(vector<int>& nums) {
int n = nums.size();
int ans = INT_MIN;
ans = maxSub(nums,0, n - 1);
return ans;
}
};
int main(){
Solution s;
vector<int> nums = {-2,1,-3,4,-1,2,1,-5,4};
cout << s.maxSubArray(nums) << endl;
return 0;
}
思路:
1.暴力:枚举起点和终点,计算区间内的和,取最大值。时间复杂度:O(n^2)
2.分治:时间复杂度:O(nlogn)
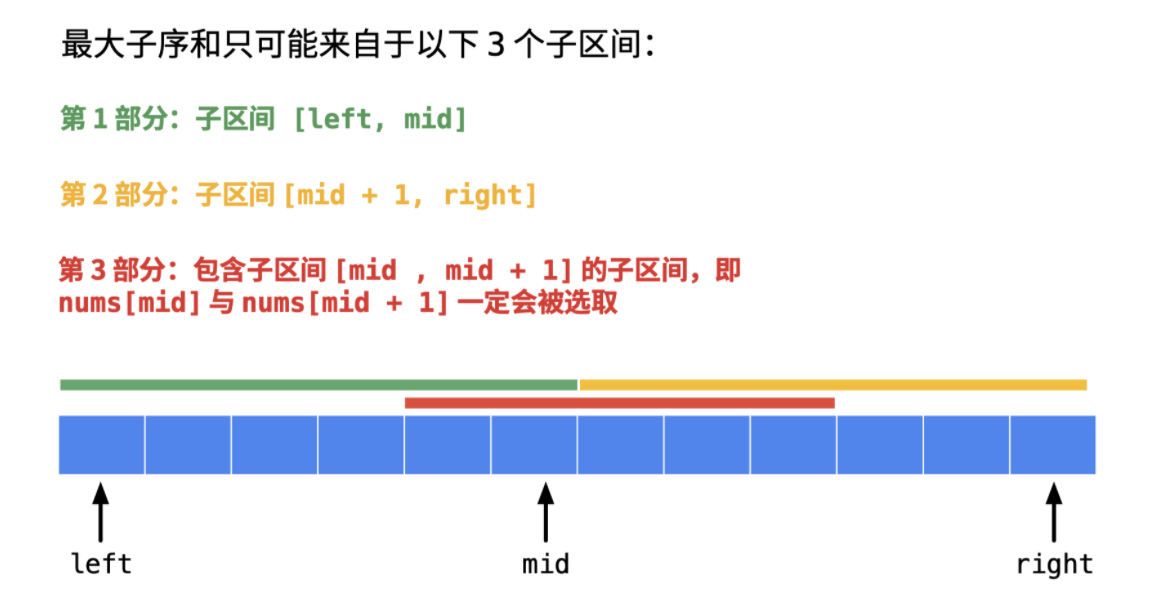
取中心点m=(l+r)/2。 和最大的区间要么出现在中心点左边,要么出现在中心点右边,要么横跨中心点。所以问题分解为求这三部分的最大区间和,然后取最大值。----分成3个独立的小问题,分治。
(1) 中心点左边的最大区间和:和原问题相同,递归。
(2) 中心点右边的最大区间和:和原问题相同,递归。
(3)横跨中心点的最大区间和:贪心求解—从中心点往左右两边延申。
从中心点不断往左延申,同时记录最大值lmax
从中心点不断往右延申,同时记录最大值rmax
横跨中心点的最大区间和:lmax+rmax
3.动态规划:线性动态规划。时间复杂度 O(n)。
状态:dp[i]=x 以第i个元素结尾的和最大的区间,最大和是 x
初始状态:dp[0]=nums[0]
转移方程:dp[i]=max(dp[i-1]+nums[i],nums[i])
最终答案:max(dp[i])