一、原因
神经网络梯度
· 假设现在有一个 层的神经网络,每层的输出为一个对输入作
变换的函数结果
· 用 来表示第
层的输出,那么有下列公式:
· 链式法则计算损失 关于某一层某个参数
的梯度:
· 注意到, 为向量,这相当于一个 d-t 次的矩阵乘法
这个传递可能造成以下问题:
· 假设每次的梯度为1.5,但随着神经网络的规模变大,往后传递过去可能就有 这么大,从而产生梯度爆炸。
· 假设每次的梯度为0.8,同样的道理,传递过去可能有 这么小,从而使模型最后的变化幅度很小,出现梯度消失。
二、梯度消失
假设用sigmoid函数作为激活函数
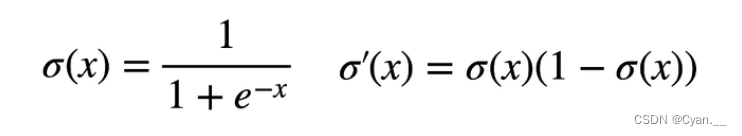
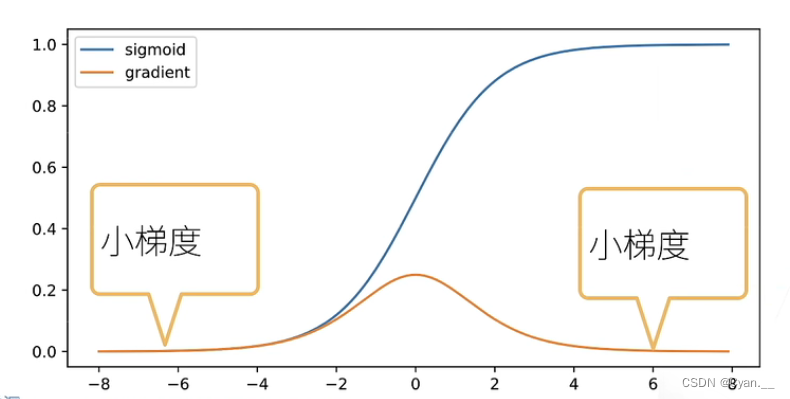
· 导数的问题是,当输入相对较大或者较小时,求导计算之后,每次向上传递的梯度会变得很小
· 累乘起来之后,这个值可能就会变得更小
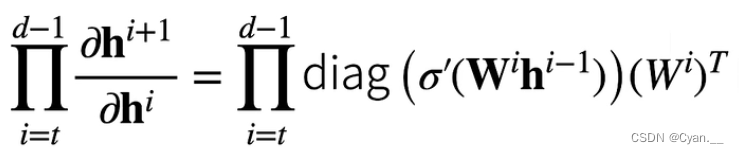
可能造成的问题:
· 梯度值非常接近0,使得模型无法训练,每次训练改变幅度非常小
· 在神经网络较深时,对于底部层尤为严重
· 反向传播时,顶部的训练可能较好,拿到的梯度较正常
· 越到底部,梯度越小,底部层无法训练,使得神经网络无法变深
三、梯度爆炸
假设我们使用ReLU函数作为隐藏层的激活函数

· ReLU激活函数的导数会使大于0的输出求导后都是1,小于等于0的输出求导后都是0
· 首先将链式法则的求导公式代入ReLU激活函数转化一下,得到下式
· 这时, 与
相乘后再在ReLU函数里求导的结果就是0或1,那么每次传递的就是
转置值
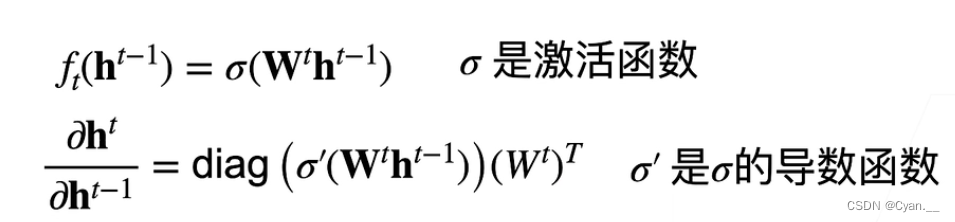
· 如果中间层 d-t 很大,那么最后累乘的结果就会很大,最终导致梯度爆炸
可能造成的问题:
· 值超过上限(如16位浮点数,可能数值上溢)
· 对学习率非常敏感
· 若学习率较大—大参数值—更大的梯度
· 若学习率较小—训练效果小
· 需要不断调整学习率