矩阵代数
共轭转置
对于矩阵
A
=
[
a
i
j
]
A=[a_{ij}]
A=[aij],共轭矩阵被定义为
A
‾
=
[
a
‾
i
j
]
\overline{A}=[\overline{a}_{ij}]
A=[aij],所以
A
A
A的共轭转置
A
‾
T
=
A
T
‾
\overline{A}^T=\overline{A^T}
AT=AT,其中
A
‾
T
\overline{A}^T
AT记为
A
∗
A^*
A∗。
(
1
−
4
i
i
2
3
2
+
i
0
)
∗
=
(
1
+
4
i
3
−
i
2
−
i
2
0
)
\begin{pmatrix}1-4\text{i}&\text{i}&2\\3&2+\text{i}&0\end{pmatrix}^*=\begin{pmatrix}1+4\text{i}&3\\-\text{i}&2-\text{i}\\2&0\end{pmatrix}
(1−4i3i2+i20)∗=
1+4i−i232−i0
其中符合如下规则
(
A
+
B
)
T
=
A
T
+
B
T
and
(
A
+
B
)
∗
=
A
∗
+
B
∗
.
(
α
A
)
T
=
α
A
T
and
(
α
A
)
∗
=
α
‾
A
∗
.
\begin{aligned}\left(\mathbf{A}+\mathbf{B}\right)^T&=\mathbf{A}^T+\mathbf{B}^T\quad\text{ and }\quad\left(\mathbf{A}+\mathbf{B}\right)^*=\mathbf{A}^*+\mathbf{B}^*.\\\\\left(\alpha\mathbf{A}\right)^T&=\alpha\mathbf{A}^T\quad\text{ and }\quad\left(\alpha\mathbf{A}\right)^*=\overline{\alpha}\mathbf{A}^*.\end{aligned}
(A+B)T(αA)T=AT+BT and (A+B)∗=A∗+B∗.=αAT and (αA)∗=αA∗.
线性系统
f
(
α
x
+
y
)
=
α
f
(
x
)
+
f
(
y
)
f(\alpha x+y)=\alpha f(x)+f(y)
f(αx+y)=αf(x)+f(y)
其中满足
(
A
B
)
∗
=
B
∗
A
∗
t
r
a
c
e
(
A
B
C
)
=
t
r
a
c
e
(
B
C
A
)
=
t
r
a
c
e
(
C
B
A
)
≠
t
r
a
c
e
(
B
A
C
)
(AB)^*=B^*A^*\\ trace(ABC)=trace(BCA)=trace(CBA)\not=trace(BAC)
(AB)∗=B∗A∗trace(ABC)=trace(BCA)=trace(CBA)=trace(BAC)
若
A
n
×
n
A_{n\times n}
An×n是非奇异矩阵,则
r
a
n
k
(
A
)
=
n
rank(A)=n
rank(A)=n,即A可以通过Gauss-Jordan方法变为单位阵
A
→
Gauss-Jordan
I
[
A
∣
I
]
→
Gauss
−
Jordan
[
I
∣
A
−
1
]
\begin{aligned} A&\xrightarrow{\text{Gauss-Jordan}}I\\ [\mathbf{A}\mid\mathbf{I}]&\xrightarrow{\text{Gauss}-\text{Jordan}} [ \mathbf{I}\mid\mathbf{A}^{-1}] \end{aligned}
A[A∣I]Gauss-JordanIGauss−Jordan[I∣A−1]
等价矩阵
若存在矩阵 P A Q = B PAQ=B PAQ=B则称A与B是等价矩阵,其中 P , Q P,Q P,Q为非奇异矩阵
若B由A矩阵可以经过行变换获得,则称B与A行等价,即
A
∼
r
o
w
B
⟺
P
A
=
B
f
o
r
a
n
o
n
s
i
n
g
u
l
a
r
P
\mathbf{A}\overset{\mathrm{row}}{\operatorname*{\sim}}\mathbf{B}\Longleftrightarrow\mathbf{P}\mathbf{A}=\mathbf{B}\quad\mathrm{for~a~nonsingular~}\mathbf{P}
A∼rowB⟺PA=Bfor a nonsingular P
若B由A矩阵可以经过列变换获得,则称B与A列等价,即
A
∼
c
o
l
B
⟺
A
Q
=
B
f
o
r
a
n
o
n
s
i
n
g
u
l
a
r
Q
\mathbf{A}\overset{\mathrm{col}}{\operatorname*{\sim}}\mathbf{B}\Longleftrightarrow\mathbf{A}\mathbf{Q}=\mathbf{B}\quad\mathrm{for~a~nonsingular~}\mathbf{Q}
A∼colB⟺AQ=Bfor a nonsingular Q
若存在一个矩阵
A
n
×
m
A_{n\times m}
An×m,其中
rank
(
A
)
=
r
\text{rank}(A)=r
rank(A)=r,则
A
∼
N
r
=
(
I
r
0
0
0
)
\mathbf{A}\sim\mathbf{N}_r=\begin{pmatrix}\mathbf{I}_r&\mathbf{0}\\\mathbf{0}&\mathbf{0}\end{pmatrix}
A∼Nr=(Ir000)
LU分解
若存在下三角矩阵 L L L与上三角矩阵 U U U,其中 L U = A LU=A LU=A,则被称为A的LU分解,其中U矩阵是高斯消元法的产物,L矩阵则对角线上是1,其中 l i j l_{ij} lij是被用于高斯消元法中消去 ( i , j ) (i,j) (i,j)位置上的数字
若在LU分解中存在0主元则无法进行LU分解,则可以利用行交换来实现A的LU分解。即 P A = L U PA=LU PA=LU
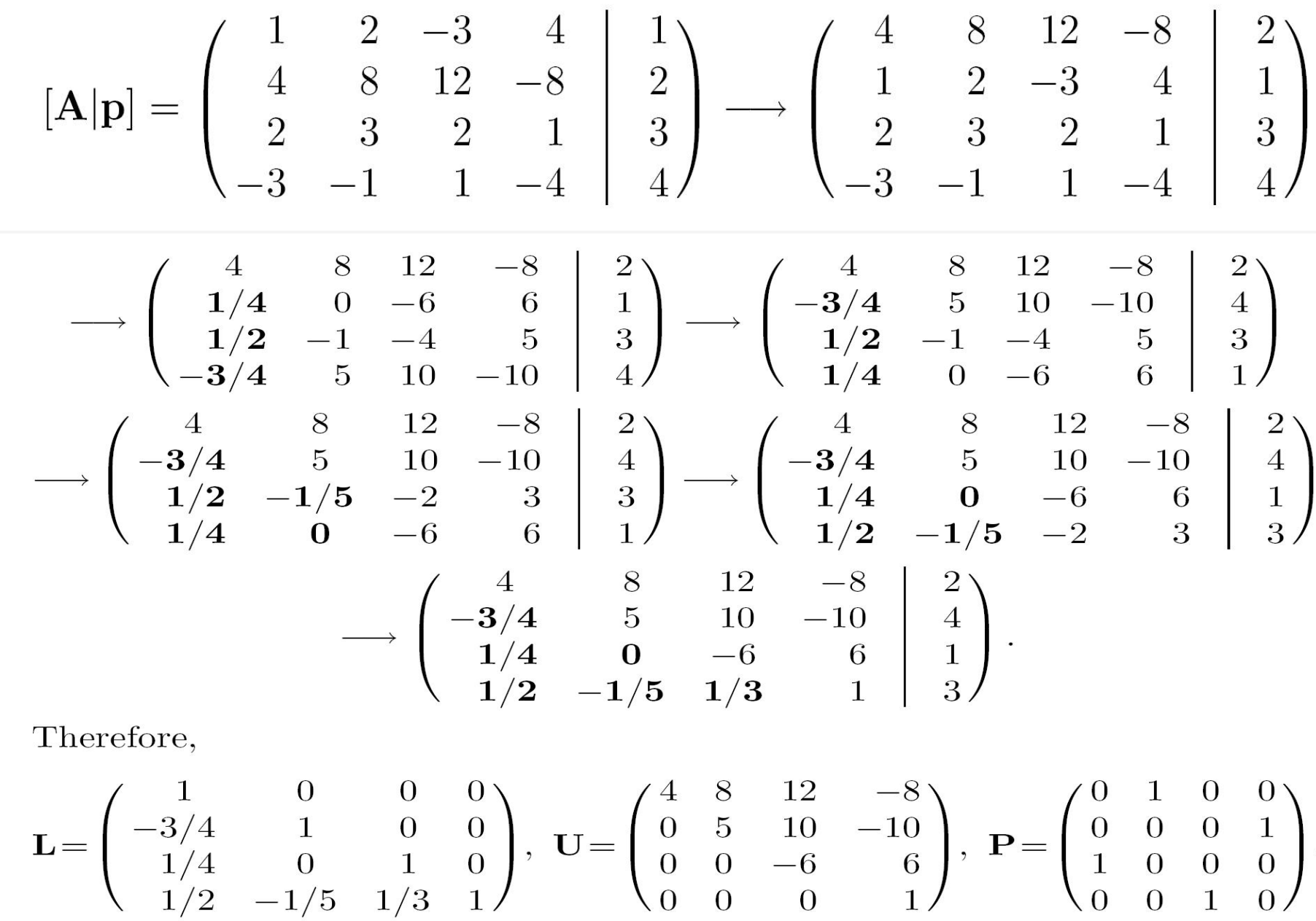
LU分解存在的条件
- A必须是非奇异矩阵
- 在约减成上三角矩阵时候,没有0主元